Кривые и поверхности в компьютерной геометрии, II
B-кривые (бета-кривые)
Основными недостатками кривых Безье являются следующие:
- смещение любой опорной точки глобально влияет на всю кривую;
- сложно обеспечить точное прохождение кривой через заданные точки (кроме крайних опорных точек, являющихся концами кривой).
Поэтому при работе с кривыми Безье часто приходиться прибегать к делению кривой Безье, т. е. по сути дела - к замене одной кривой другими. Поэтому естественным образом возникает задача построения такого класса кривых, который бы позволял избежать недостатков 1), 2) и решать соответствующие задачи управления кривой путем изменения управляющих параметров кривой, а не путем ее замены на другие кривые.
Вспомним, что рациональная кривая Безье, построенная по точкам  с весами
с весами 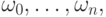 определялась формулой
определялась формулой
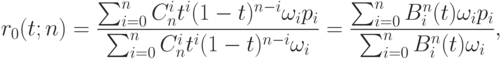 |
( 6.1) |
где 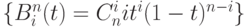 - базис Бернштейна на [0,1].
- базис Бернштейна на [0,1].
Из формулы (6.1) видно, что глобальное влияние каждой опорной точки 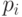 на всю кривую происходит из-за того, что каждая из функций
на всю кривую происходит из-за того, что каждая из функций 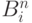 не равна нулю на всем интервале (0,1). Если бы вместо функций Бернштейна в формуле (6.1) выступали функции с локальными носителями, существенно меньшими, чем область определения параметра кривой
не равна нулю на всем интервале (0,1). Если бы вместо функций Бернштейна в формуле (6.1) выступали функции с локальными носителями, существенно меньшими, чем область определения параметра кривой 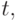 то удалось бы как локализовать влияние отдельной точки на всю кривую, так и добиться (за счет выбора таких функций) прохождения кривой через некоторую заданную точку.
то удалось бы как локализовать влияние отдельной точки на всю кривую, так и добиться (за счет выбора таких функций) прохождения кривой через некоторую заданную точку.
Поэтому поставим задачу следующим образом. Пусть даны опорные точки 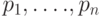 с весами
с весами 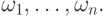 Определим кривую
Определим кривую 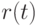 по формуле
по формуле
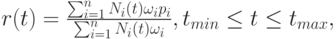 |
( 6.2) |
где 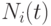 - набор кусочно-полиномиальных функций таких, что
- набор кусочно-полиномиальных функций таких, что
-
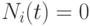 при
при ![t\notin [a_i, b_i]\subset [t_{min}, t_{max}]](/sites/default/files/tex_cache/f1196cf2272894ea0da7f1298cafc4fc.png) ;
; -
для любой гладкой функции
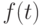 существует линейная комбинация
существует линейная комбинация 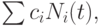 интерполирующая функцию
интерполирующая функцию 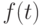 в заданных узлах
в заданных узлах 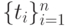
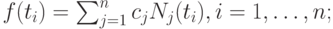
-
 для каждого
для каждого ![t \in [t_{min},t_{max}].](/sites/default/files/tex_cache/ee40d6294534b83daf437f1b63d1a33c.png)
Последнее условие вводится для того, чтобы в случае совпадения всех опорных точек кривая превращалась бы в ту же точку.
Решение поставленной задачи основывается на понятии разделенных разностей и называется В-кривой. В-кривые обобщают кривые Безье.
Разделенные разности
Пусть имеется гладкая на каждом отрезке ![[t_i,t_{i+1}]](/sites/default/files/tex_cache/b4225e7e09f1ed17d0fb67701813c94b.png) функция
функция 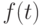 и фиксированы некоторые значения
и фиксированы некоторые значения  переменной
переменной  (не обязательно различные и не обязательно упорядоченные по возрастанию или убыванию
(не обязательно различные и не обязательно упорядоченные по возрастанию или убыванию  ). Мы также будем рассматривать переменное значение
). Мы также будем рассматривать переменное значение 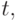 которое будем считать первым в последовательности. Поскольку оно предшествует значению
которое будем считать первым в последовательности. Поскольку оно предшествует значению 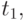 припишем ему индекс 0 (хотя в большинстве случаев будем обозначать его просто
припишем ему индекс 0 (хотя в большинстве случаев будем обозначать его просто  без индекса):
без индекса): 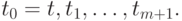 Обозначим
Обозначим 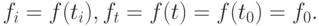 Определим оператор правого сдвига
Определим оператор правого сдвига  :
:
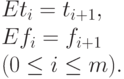
Определение 6.1.1. Разделенной разностью функции 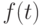 в узле
в узле 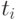 порядка
порядка 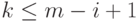 называется величина
называется величина
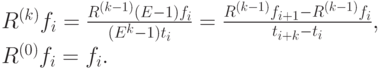 |
( 6.3) |
Разделенная разность является дискретным аналогом операции дифференцирования соответствующего порядка.
При этом если 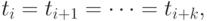 то в правой части (6.3) появляется отношение вида
то в правой части (6.3) появляется отношение вида 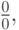 которое по определению полагается равным
которое по определению полагается равным
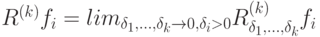
где 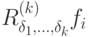 определяется по возмущенным узлам
определяется по возмущенным узлам 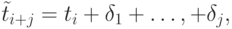 где
где 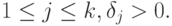
Теорема 6.1. Если 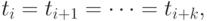 то
то
Пример 6.1.1. Разделенная разность пятого порядка функции  как функция первого узла (программа не вычисляет производные при совпадении узлов):
как функция первого узла (программа не вычисляет производные при совпадении узлов):
In[1]:=
DynamicModule [{n = 5, tt, F, h, L, t, t2, t3, t4, t5, f, p, S, z},
f [t_] := Cos [t] ;
Manipulate[
tt = Join[{t} , ss] ;
p[i_, s_] := Apply [ Times , (s - tt [ [#] ] ) &/@ Drop [Range [n] , {i}]];
S = Flatten [Table [Table [ss[ [j] ] - ss [ [i] ] , {i, 1, j - 1}] ,
{j, 2, Length[ss]}]];
z = Apply [ Times , S ] ;
If[z ? 0,
L = Table [l/p[i, tt[[i]]] , {i, 1, n} ] ;
F = Table [f [tt[[i]]], {i, 1, n}];
h=F.L/. t -> 0;
Show[
Plot[{f [t] , F.L/h), {t, -20, 20), PlotRange -> {{-25, 25} , {-10, 10}}] ,
Graphics[{Red, PointSize[Large],
Point[Table[{ss[[i]], 0} , {i, 1, Length[tt] - 1}]] ,
Text[ToString[#] , {ss [[#]]+1.2 , 0}] &/@ Range [4] , Axes -> True} ]
]
Show[Graphics[Text["Узлы совпадают"],
PlotRange -> {{-25, 25}, {-20, 20}}]]
]
{{ss, {-7.2, 0.7, 5.2, 12.0}, "Узлы"},
With[{r = Range[1, Length[tt] -1]},
Grid[
{Spacer [3] , Subscript [Style [" t" , Italic], # - 1] ,
Slider [Dynamic@ss[[.#l]] , {-20, 20, .01}, Appearance -> "UpArrow" ,
ImageSize -> {200, 12}], Dynamic@ss [[#1]] } & /@ r] ] &,
ControlPlacement -> Bottom} , TrackedSymbols -> {ss} ,
SaveDef initions -> True ] ]Задача 6.1.1. Обратите внимание, что разделенная разность быстро убывает при удалении вправо и влево от крайних узлов. Каков порядок этого убывания?
Задача 6.1.2. Написать программу, которая бы учитывала совпадение узлов.

