Кривые и поверхности в компьютерной геометрии, II
Усеченная степенная функция
Пусть  - целое число. Рассмотрим функцию
- целое число. Рассмотрим функцию  При фиксированном
При фиксированном  функция
функция 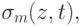 рассматриваемая как функция
рассматриваемая как функция 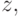 называется усеченной степенной функцией.
называется усеченной степенной функцией.
Лемма 6.1. Для производных усеченной степенной функции справедливы формулы
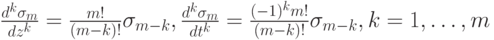
Обозначим через ![f[t_1,\dots, t_k]](/sites/default/files/tex_cache/e4cdbf432ed8eb47b031fdf1c223f7bc.png) разделенную разность порядка
разделенную разность порядка  функции
функции 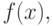 построенную по узлам
построенную по узлам  Фиксируем набор узлов
Фиксируем набор узлов 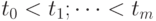 и рассмотрим функцию
и рассмотрим функцию  ,](/sites/default/files/tex_cache/fec873b645c29952a60fb6f33a1caa2f.png) где разделенная разность
где разделенная разность ](/sites/default/files/tex_cache/7a72b0960baaacbf97fab13611cc3b9b.png) вычисляется от
вычисляется от 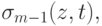 рассматриваемой как функция
рассматриваемой как функция  при фиксированном
при фиксированном 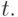
Лемма 6.2. Пусть  Тогда
Тогда  если
если  или
или 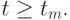
Замечание 6.1.1. Из леммы 6.2 вытекает, что ](/sites/default/files/tex_cache/1a132f61374cc77a2b6384b3888f092c.png) является непрерывной при
является непрерывной при  функцией параметра
функцией параметра 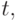 отличной от нуля лишь на
отличной от нуля лишь на 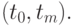
Пример 6.1.2. Разделенная разность пятого порядка усеченной кубической функции. Разделенная разность вычисляется от 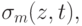 рассматриваемой как функция
рассматриваемой как функция  при фиксированном
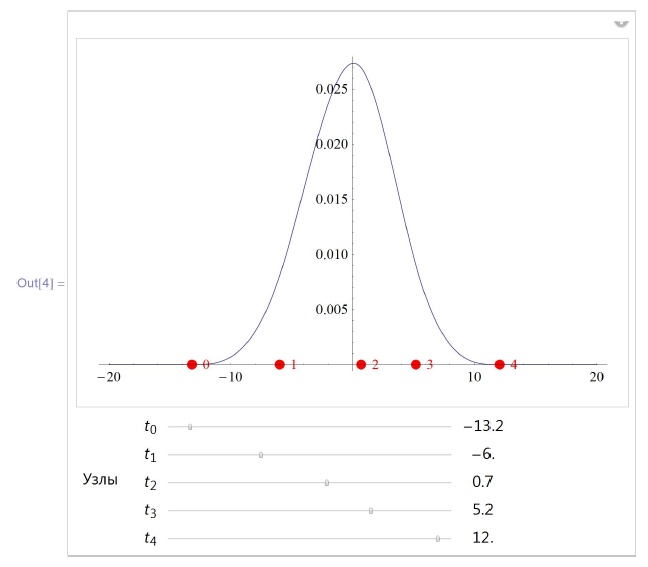
при фиксированном 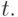 Программа демонстрирует равенство нулю разделенной разности при всех
Программа демонстрирует равенство нулю разделенной разности при всех 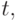 лежащих левее и правее всех узлов.
лежащих левее и правее всех узлов.
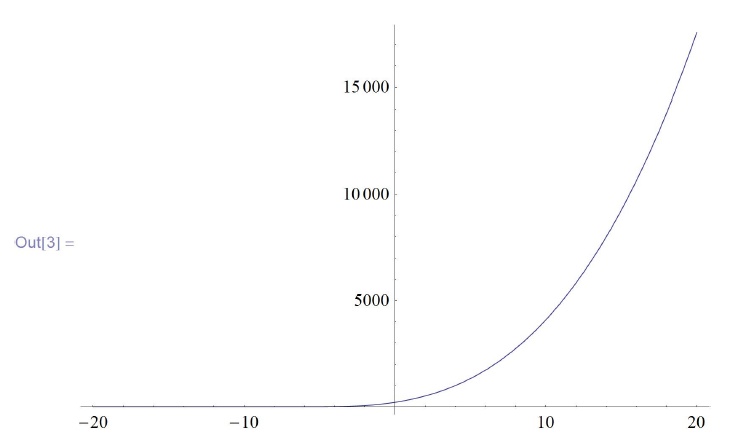
In[2]:=f[t_, z_]:=If[t < z, (z-t)^3, 0];
Plot[f[-6, z], {z, -20, 20}]In[4] :=DynamicModule[ {h, z, t, st, M, G, i, x, y} ,
h[x_, y_] : = If [x < y, (y - x)^3, О] ;
Manipulate[
p[i_, s_] := Apply [Times, (s-st[[#]]) & /@
Drop[Range[Length[st]], {i}]];
z = Apply [Times, (st[ [#] ] - st[ [#+ 1] ]) & /@
Range [Length [st] - 1] ] ; If [z ? 0,
M = Table [1 /p[i, st[[i]]], {i, 1, Length [st] }] ;
G = Table[h[t, st[[i]]], {i, 1, Length[st]}];
Show[If[OrderedQ[st], Plot[G.M, {t, -20, 20}],
Do [If [st[[i - 1]] > st[[i]], st[[i- l]] = st[[i]] ,
{i, 2, Length[st]}] ; Plot[G.M, {t, -20, 20}]],
Graphics[{Red, PointSize[Large] ,
Point[Table[{st[[i]], 0}, {i, 1, Length[st]}]],
Text[ToString[#-1] , {st[[#]] +1.2, 0}] & /@
Range [ 5 ] , Axes -> True} ] ] ,
Show[Graphics[Text["Узлы совпадают"],
PlotRange -> {{-25, 25} , {-20, 20}}] ] ] ,
{{st, {-13.2, -6.0, 0.7, 5.2, 12.0}, "Узлы"},
With[{r= Range[l, Length[st]]},
Grid[{Spacer[3], Subscript[
Style["t", Italic], #-1],
Slider [Dynamic@st[[#1]] , {-15, 13, .01},
Appearance -> "UpArrow" , ImageSize -> {200, 12} ] ,
Dynamic@st|[#l]l} &/@ r] ] &,
ControlPlacement -> Bottom} , TrackedSymbols ->{st},
SaveDefinitions -> True] ]Задача 6.1.3. Написать программу, которая бы учитывала совпадение узлов.
B-сплайны
На основе разделенных разностей мы будем строить весовые функции 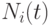 в формуле (6.2) с целью обобщения рациональных кривых Безье:
в формуле (6.2) с целью обобщения рациональных кривых Безье:
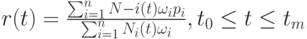
Определение 6.1.2. Нормированным B-сплайном m-го порядка  для неубывающей последовательности узлов
для неубывающей последовательности узлов  отсчитываемой от первого узла
отсчитываемой от первого узла 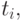 называется функция
называется функция
](/sites/default/files/tex_cache/41b9558dee2e9feb314fde0bcc55e06a.png)
Соответственно, ненормированным B-сплайном 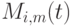 называется функция
называется функция
.](/sites/default/files/tex_cache/8d28180228a92d96493e2710cbe09163.png)
Определение 6.1.3. Нормированным B-сплайном m-го порядка 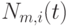 для неубывающей последовательности узлов
для неубывающей последовательности узлов  отсчитываемой от последнего узла
отсчитываемой от последнего узла 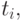 называется функция
называется функция
.](/sites/default/files/tex_cache/9048e23781779a8089f06eaeb12f9efd.png)
Соответственно определяется и ненормированный B-сплайн 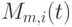 :
:
.](/sites/default/files/tex_cache/418366e7ce4ae0c4acbbb84a1899e62a.png)
Замечание 6.1.2. Если порядок B -сплайна определять не числом узлов минус единица, а степенью усеченной функции (как многочлена t ), то введенные выше B -сплайны будут иметь (по определению) порядок не m, а (m - 1). В этом случае для них применяются другие обозначения: 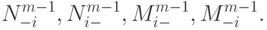 При этом
При этом
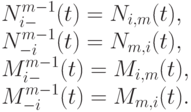
И те и другие обозначения присутствуют в литературе по B -кривым. Мы будем пользоваться первыми. В Mathematica используются вторые.
Рассмотрим (для простоты) бесконечную в обе стороны последовательность неубывающих узлов 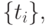 где
где 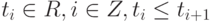 для любого
для любого 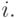 Фиксируем
Фиксируем  Тогда определены множества B -сплайнов: сплайны
Тогда определены множества B -сплайнов: сплайны  привязаны к узлу
привязаны к узлу  как к первому узлу, сплайны
как к первому узлу, сплайны 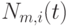 привязаны к узлу
привязаны к узлу  как к последнему узлу
как к последнему узлу 
Лемма 6.3. Если ![t \in [t_j,t_{j+1}],](/sites/default/files/tex_cache/54fc7db747593e9a828ed85159ed5126.png) то среди функций
то среди функций  и
и 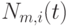 только m функций в каждом из этих двух классов могут быть отличны от нуля в точке
только m функций в каждом из этих двух классов могут быть отличны от нуля в точке 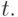 А именно, отличны от нуля в точке
А именно, отличны от нуля в точке  могут быть лишь следующие функции:
могут быть лишь следующие функции:
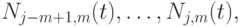
и
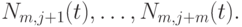
Лемма 6.4. Для любого  имеет место
имеет место
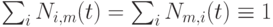
Теорема 6.2 (формула Кокса - де Бура). Справедливы следующие формулы для ненормированных B-сплайнов при любых 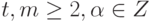 и
и 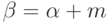 :
:
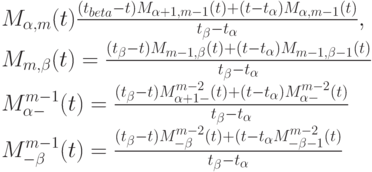 |
( 6.4) |
Здесь ненормированные B-сплайны первого порядка равны по определению разделенным разностям функции 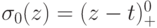 :
:
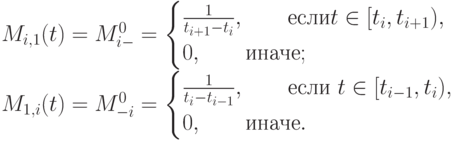 |
( 6.5) |
Теорема Кокса - де Бура позволяет вычислять B -сплайны рекуррентно с использованием формул (6.4) и (6.5).
Следствие 6.1. Пусть имеется произвольная последовательность (не обязательно неубывающих) узлов 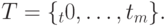 Пусть среди них есть 2 неравных друг другу узла
Пусть среди них есть 2 неравных друг другу узла 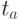 и
и 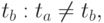 где
где 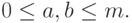 Обозначим
Обозначим
![M^T(t) =\sigma_{m-1}[T] = \sigma_{m-1}[t_0,\dots ,_tm],\\
M^{T/a}(t) = \sigma_{m-2}[T\ a] = \sigma_{m-2}[t_0, \dots ,\hat t_a, \dots ,t_m],\\
M^{T/b}(t) =\sigma_{m-2}[T\b] =\sigma_{m-2}[t_0, \dots ,\hat t_b, \dots ,t_m],\\
p_{ab}(t) =\frac{t_b-t}{t_b-t_a}, q_{ab}(t)=\frac{t-t_a}{t_b-t_a}, (p_{ab}+q_{ab} \evqiv 1)](/sites/default/files/tex_cache/f67a5311d8d51ce13c0f347166686d05.png)
где "домиком" отмечены отброшенные узлы. Тогда
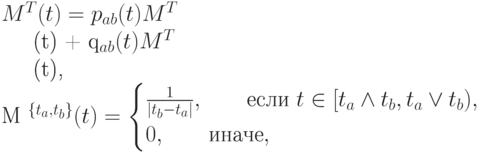
где 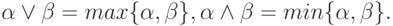
Следствие 6.2. B - сплайны - неотрицательные функции:
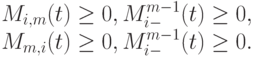
Следствие 6.3. Для нормированных B-сплайнов формулы Кокса - де Бура принимают вид 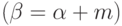 :
:
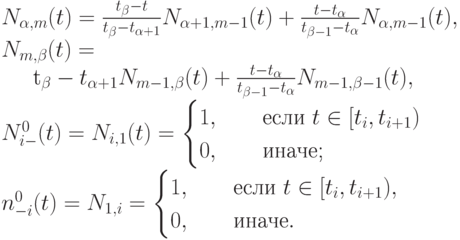
Для сокращения объема вычислений следует сначала вычислить ненормированные B -сплайны нужного порядка по формулам Кокса - де Бура, а затем нормировать их. Если требуется вычислить все ненулевые B -сплайны порядка m для ![t \in [t_i,t_{i+1}]](/sites/default/files/tex_cache/e52b1cb9ecba0654b61b4a6b2e0365f3.png) в неубывающей последовательности узлов
в неубывающей последовательности узлов 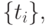 то вычисления производятся по схеме
то вычисления производятся по схеме
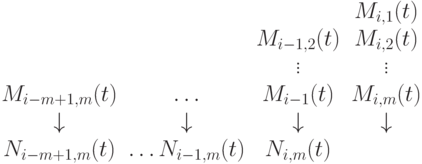
Аналогичная схема вычислений применяется для B -сплайнов остальных трех типов.
Следствие 6.4. Для любых  и
и 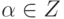 функции
функции  и
и 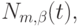 где
где 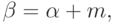 построенные по неубывающей последовательности узлов
построенные по неубывающей последовательности узлов  являются непрерывными
являются непрерывными  раза дифференцируемыми функциями, обращающимися в ноль вне отрезка
раза дифференцируемыми функциями, обращающимися в ноль вне отрезка ![[t_{\alpha},t_{\beta}].](/sites/default/files/tex_cache/31078404bff279093353e4cefba5e897.png) На отрезке
На отрезке ![[t_i,t_{i+1}]](/sites/default/files/tex_cache/b4225e7e09f1ed17d0fb67701813c94b.png) они имеют производные до порядка
они имеют производные до порядка  включительно. Функции
включительно. Функции  и
и 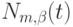 зависят (как от параметров) лишь от значений узлов
зависят (как от параметров) лишь от значений узлов 
Задача 6.1.4. С помощью встроенной функции в пакет Mathematica ![BSplineBasis[\{m,{t_0, \dots ,t_n\}\}, i, t] ,](/sites/default/files/tex_cache/b8fe46a8e018f0a243ddbd23c27506c7.png) вычисляющей тот из
вычисляющей тот из  нормированныx B -сплайнов
нормированныx B -сплайнов  порядка
порядка 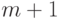 (или m при втором способе определения порядка, см. выше), который привязан справа к i -му (
(или m при втором способе определения порядка, см. выше), который привязан справа к i -му ( 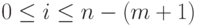 ) узлу из расширенного множества неубывающих узлов
) узлу из расширенного множества неубывающих узлов  (см. определение ниже), наглядно изучить ненормированные и нормированные B -сплайны, привязанные к узлам справа. Обратите внимание, что в Mathematica узлы в расширенном множестве нумеруются начиная с нуля. Соответственно, в Mathematica B -сплайны в базисе нумеруются с нулевого до n - (m + 1) -го.
(см. определение ниже), наглядно изучить ненормированные и нормированные B -сплайны, привязанные к узлам справа. Обратите внимание, что в Mathematica узлы в расширенном множестве нумеруются начиная с нуля. Соответственно, в Mathematica B -сплайны в базисе нумеруются с нулевого до n - (m + 1) -го.
Замечание 6.1.3. При работе с нижеследующей программой обратите внимание, что при совпадении первых m + 1 узлов значение нулевого (самого первого) нормированного B -сплайна из базиса в нулевом (самом первом) узле становится равно 1, тогда как все остальные B -сплайны базиса обращаются в этом узле в ноль. Это значит, что когда такой базис из нормированных B -сплайнов используется для вычисления радиус-вектора B -кривой (аналогично базису Бернштейна для кривых Безье), получившаяся кривая будет начинаться в своей крайней левой опорной точке. Аналогично, при совпадении последних m + 1 узлов расширенного множества, последний сплайн базиса в последнем узле примет значение 1, а остальные будут равны в нем нулю, и, следовательно, правый конец соответствующей кривой будет находиться в ее последней опорной точке. См. ниже теорему 6.3, в формулировке которой порядок B -сплайна m соответствует значению m + 1 в обозначениях Mathematica (как уже говорилось, Mathematica использует второй способ определения порядка B -сплайна, а значит, уменьшает его на единицу по сравнению с тем способом, который используем мы).
Задача 6.1.5. Написать программу на пакете Mathematica, вычисляющую B -сплайны 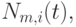 привязанные к узлам слева.
привязанные к узлам слева.
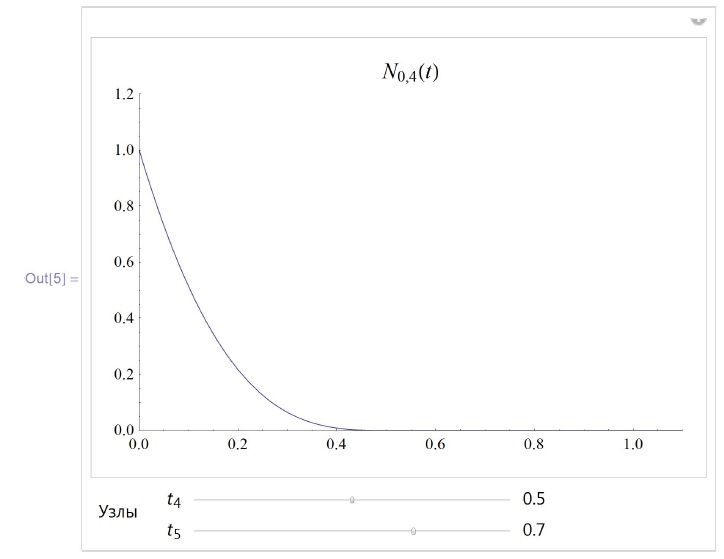
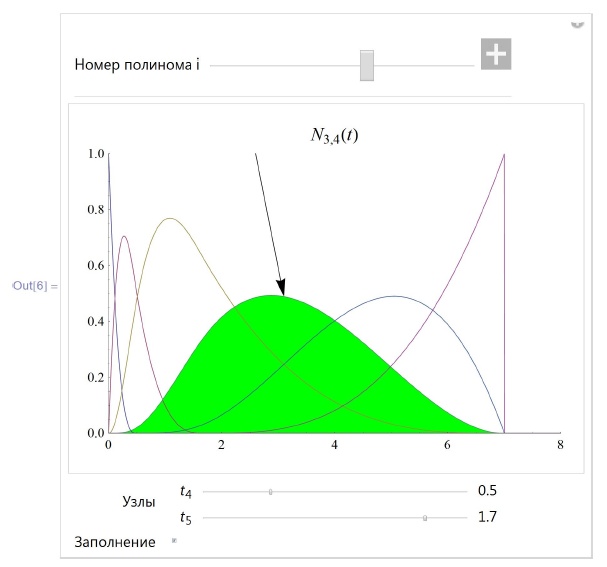
Пример 6.1.3. Следующие две программы строят графики B -сплайнов, привязанных к узлам справа. В данном примере n = 9, то есть расширенное множество узлов состоит из 10 точек, начиная с нулевой, а m = 3, то есть порядок B -сплайна при принятом нами определении равен 4.
In[5]:=
DynamicModule [ {m = 3, i, tt, knots} ,
For [i = 1, i Sm + 1, i++, tt [i] = 0] ; (*m+l начальных узло равны 0*)
tt[5] = 4; tt[6] = 4; tt[7] = 6; tt[8] = 9; :*задали m+1 конечных узлов*)
Manipulate [
knots = Join [Table [tt[i] , {i, 1, m + 1}], ss, Table [tt[j] , { j , m + 2 , 2 m + 2} ] ] ;
Show[ If[orderedQ[ss] , Plot [BSplineBasis [ {m, knots}, 0, t] ,
{t, knots[[1]] , 1.1},
PlotRange -> {{0, 1.1} , {0, 1.2}}, PlotLabel -> Style [N0,m+i [t] , 14] ] ,
Do [If [ss[[i - 1]] > ss[[1]] , ss[[i - 1]] = ss[[i]] , {i, 2, Length [ss] }] ,
Plot[BSplineBasis[{m, knots}, 0, t],
{t, knots[[1]1 , knots[[Length[knots]]] +1} ,
PlotRange -> + {{0, 1.1}, {0, 1. 2} }], PlotLabel -> Style [N0, m+1 [t] , 14]
]], {(ss, {0.5, 0.7}, "Узлы"},
With[(r = Range[1, Length[ss]]} ,
Grid[
{Spacer[3] , Subscript[Style["t", Italic] , # + m] ,
Slider [Dynamic@ ss[[#l]] , {0, 1, .01}, Appearance -> " UpArrow" ,
ImageSize -> {200, 12}], Dynamic@ss[el]]} &/@ r] ] &,
ControlPlacement -> Bottom} , TrackedSymbols -> {ss} , SaveDefinitions -> True 1 ]]In|6] :=DynamicModule [{m = 3, n = 9, i, j , tt, knots, a) ,
For [i = 1, i <= m+1, i + +, tt[i] = 0] ;
(*m+l начальных уело равны 0*)
For[j = 1, j im + 1, j++, tt[n-j] = 7] ;
(*задали m+1 конечных узлов*)
Manipulate[knots - Join[
Table [tt[i] , {i, 1, m + 1}], ss,
Table [tt[j] , {j, m + 2, 2m + 2}]] ;
a = (knots[[1]] +knots[[n]]) /2;
Show[If[OrderedQ[ss], Plot[Evaluate[
Table[BSplineBasis[{m, knots}, 1, t] ,
{1, 0, n-m-1}]], {t, knots [[1]], 8},
PlotRange -> { {knots [ [1] ] , 8}, {0, 1}},
Filling -> If [fill,
{i +1 -> {Axis, {Opacity! -15] , Green}}} , None] ,
PlotLabel -> Style [Hi, m+1 [t] , 14]],
Do [If [ss[[i - 1]] > ss[[i]] , ss[[i - 1]] = ss[[i]] ],
{i, 2, Length[ss]}];
Plot[Evaluate[Table[BSplineBasis[{m, knots}, 1, t] ,
{1, 0, n-m-1}]], {t, knots [[1]], 8},
PlotRange -> { {knots [ [1] ], 8}, {0, 1}},
Filling -> If [fill,
{i + 1 -> {Axis, {Opacity[ -15] , Green}}} , None] ,
PlotLabel -> Style [Ni, т+1 [t] , 14]] ] ,
Graphics[Arrow[{{2.5, 1.1},
, {i + 0.1, BSplineBasis[{m, knots}, i, i + 0.1]}}] ] ,
], {{i, 3, " Номер полинома i"}, 0, n-m-1, 1},
Delimiter, {{ss, {0.5, 1.7}, "УЭлы"},
With[{r=Range[1, Length[ss]]}, Grid[{Spacer[3],
Subscript[Style["t", Italic], # + m] ,
Slider [Dynamic@ss[[#l]], {0, 2, .01},
Appearance -> "UpArrow" , ImageSize -> {200 , 12} ] ,
Dynamic@ss|[#l]]} &/@r]] &,
ControlPlacement -> Bottom} ,
{{fill, True, "Заполнение"}, {True, False),
ControlPlacement -> Bottom} , SaveDefinitions -> True] ]