Первое знакомство с пакетом Mathematica
В пакет  встроено подробное описание (
встроено подробное описание ( ). Чтобы в него попасть, нажмите
). Чтобы в него попасть, нажмите  или войдите через меню
или войдите через меню  .
.
После запуска программы на экране появляется несколько независимых окон. Вдоль верхней части экрана расположено меню. Слева - рабочее окно. Можно открыть много рабочих окон, выполнив в меню команду  . Как видно из названия команды, рабочее окно называется
. Как видно из названия команды, рабочее окно называется  .
.
Если в рабочее окно ввести произвольный символ, то этот символ отобразится в окне, а справа появится вертикальная скобка, ограничивающая текущее рабочее поле. При дальнейшем вводе новые символы будут также отображаться в рабочем поле. Если произойдет переход на следующую строку, правая скобка расширится. Эта скобка указывает на независимую область, в которой можно расположить команды языка  и одновременно их выполнить. Область, ограниченная скобкой, называется клеткой (
и одновременно их выполнить. Область, ограниченная скобкой, называется клеткой (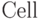 ). Если стать на последней строке клетки и нажать на стрелочку вниз, или же стать на первой строке клетки и нажать на стрелочку вверх, то курсор превратится в горизонтальную линию, расположенную рядом с клеткой. Если опять ввести символ, то появится новая клетка, в которую также можно вводить текст. Кроме того, переходить от клетки к клетки, а также позиционировать курсор между клетками можно с помощью мышки.
). Если стать на последней строке клетки и нажать на стрелочку вниз, или же стать на первой строке клетки и нажать на стрелочку вверх, то курсор превратится в горизонтальную линию, расположенную рядом с клеткой. Если опять ввести символ, то появится новая клетка, в которую также можно вводить текст. Кроме того, переходить от клетки к клетки, а также позиционировать курсор между клетками можно с помощью мышки.
В клетки можно вводить произвольные выражения ( ) и вычислять (
) и вычислять (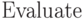 ) их. Для вычисления нужно, находясь внутри клетки, выполнить команду
) их. Для вычисления нужно, находясь внутри клетки, выполнить команду  (здесь и всюду ниже знак + обозначает одновременное нажатие клавиш). Поместите курсор внутрь следующей клетки, в которой написано
(здесь и всюду ниже знак + обозначает одновременное нажатие клавиш). Поместите курсор внутрь следующей клетки, в которой написано  , и выполните
, и выполните 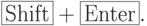
![In[1]:=2 + 2 \\
Out[1] = 4](/sites/default/files/tex_cache/5dbcde8e609c869fee8adcdfd7c40339.png)
После выполнения команды  слева от выражения появится
слева от выражения появится ![\text{In[1]}](/sites/default/files/tex_cache/03c0b355171a7221e5d54d6ead810ead.png) , нумерующее последовательно выполняющиеся команды. Кроме того, возникнет еще одна клетка с результатом, который будет помечен
, нумерующее последовательно выполняющиеся команды. Кроме того, возникнет еще одна клетка с результатом, который будет помечен ![\text{Out[1]}](/sites/default/files/tex_cache/8cf435dec24bc1a2713fbbab7f636f53.png) . Заметим, что клетка ввода и вывода объединены в одну большую клетку. Вы можете манипулировать результатом многими способами. Один из них - использование символа
. Заметим, что клетка ввода и вывода объединены в одну большую клетку. Вы можете манипулировать результатом многими способами. Один из них - использование символа  , которому присвоен результат последней выполненной команды; последовательности
, которому присвоен результат последней выполненной команды; последовательности 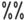 - результат выполнения предпоследней команды;
- результат выполнения предпоследней команды; 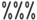 - предпредпоследней и т.д., а также
- предпредпоследней и т.д., а также 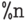 - результат выполнения команды с номером
- результат выполнения команды с номером  .
.
Основные операции пакета Mathematica
Объекты, которыми оперирует  :
:
- числа (
 ), например,
), например, 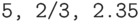 ;
; - символы (
 ), например,
), например,  ;
; - строки (
 ), например,
), например, 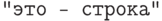 ;
; - выражения (
 ), например,
), например, 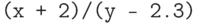 .
.
Замечание
Имеется несколько способов визуализации одного и того же выражения, например,
![\tt
(1+2.-5.77*3.8)/((3.2-0.1)\^\,\!(1/2)+6\^\,\!2) \\ \\ \tt
(1+2.-5.77 3.8)/(Sqrt[3.2-0.1]+6\^\,\!2) \\ \\
Times[ \\
\phantom{Tim}Plus[1, 2., Times[-1, Times[5.77, 3.8]]], \\
\phantom{Tim}Power[Plus[Power[Plus[3.2, -0.1], Times[1, Power[2, -1]]], \\
\phantom{Tim}\phantom{Power[Plus[}Power[6, 2]], -1]]](/sites/default/files/tex_cache/2e0011682bc92124f21f080acffb9d80.png)
В последнем случае ![\text{\tt Times[x,y]}](/sites/default/files/tex_cache/4a11e7dfd7f6214b0e8d40932239a435.png) обозначает произведение
обозначает произведение  и
и  ,
, ![\text{\tt Plus[x,y]}](/sites/default/files/tex_cache/b71f5d8b5dbd0f282b8d1e031aef6031.png) - их сумму, а
- их сумму, а ![\text{\tt Power[x,y] - x}](/sites/default/files/tex_cache/05550ad527e214eb389c4f4261cc7fd4.png) в степени
в степени  .
.
Три типа визуализации выражений
Cтаньте в клетку, вид которой хотите изменить, и выполните соответствующую команду:
 :
:
![\tt In[2]:= (1 + 2. - 5.77*3.8) / (Sqrt[3.2 - 0.1] + 6 \^\,\! 2) \\ \\ \tt
Out[2] =-0.501209](/sites/default/files/tex_cache/9541025a7e174750da9cba4f1114d505.png)
 :
:
![\tt In[3]:=$\frac{1+2.-5.77 \times 3.8}{\sqrt{3.2-0.1}+6^2}$\\ \\ \tt Out[3]=-0.501209](/sites/default/files/tex_cache/2bff9ad3e51070451539b6ae04a6ecb3.png)
 :
:
![\tt In[4]:=$\frac{1+2.-5.77 \times 3.8}{\sqrt{3.2-0.1}+6^2}$\\ \\ \tt Out[4]=-0.501209](/sites/default/files/tex_cache/b5347debfbd87939f373b4ff154d8400.png)
Ввод с клавиатуры в StandardForm
Выражения в  можно получать сразу. Для этого следует использовать или
можно получать сразу. Для этого следует использовать или  + клавиша,
+ клавиша,  -команда-
-команда-  , или вспомогательные панели
, или вспомогательные панели  . Например,
. Например,  - дробь
- дробь 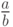 ,
,  - радикал
- радикал 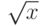 ,
,  - верхний индекс, как у
- верхний индекс, как у 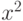 ,
,  - нижний индекс, как у
- нижний индекс, как у  .
.
Далее,  - число
- число  ,
,  - число
- число  ,
,  - мнимая единица
- мнимая единица  ,
,  - интеграл
- интеграл 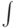 ,
,  - сумма
- сумма  ,
, 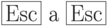 - альфа
- альфа  ,
, 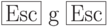 - гамма
- гамма  ...
...
Все выражения являются композицией атомарных объектов-выражений (чисел, символов и строк) и выражений вида f[x,y,...]
Выражение
![\tt
In[5]:=(1 + 2. - 5.77*3.8)/((3.2 - 0.1)\^\,\!(1/2) + 6\^\,\!2) \\ \\ \tt
Out[5]=-0.501209](/sites/default/files/tex_cache/6c37e459e8b9470a30c7560c329740c6.png)
в действительности имеет вид
![\tt
In[6]:=Times[Plus[1,2.', Times[-1, Times[5.77', 3.8']]], \\
\phantom{In[6]:=T}Power[ \\
\phantom{In[6]:=T}\phantom{P}Plus[Power[Plus[3.2',-0.1'], Times[1, Power[2,-1]]], \\
\phantom{In[6]:=T}\phantom{PP}Power[6, 2]], -1]] \\ \\ \tt
Out[6]=-0.501209](/sites/default/files/tex_cache/ecd1ff6cd13beb32fb43b3af2225e1cf.png)
Основная работа пакета Mathematica - вычисление (Evaluation) выражений
Чтобы вычислить выражение, поместите курсор внутрь содержащей его клетки и выполните команду 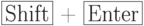 :
:
![\tt
In[7]:=(1 + 2. - 5.77*3.8)/((3.2 - 0.1)\^\,\!(1/2) + 6\^\,\!2) \\ \\
Out[7]=-0.501209](/sites/default/files/tex_cache/5d1a3fe1a63bd205ed1575861b7dabe3.png)
Арифметические операции  ; знак
; знак  можно не писать (вместо него - пробел, который
можно не писать (вместо него - пробел, который  в некоторых случаях автоматически заменяет соответствующим значком):
в некоторых случаях автоматически заменяет соответствующим значком):
![\tt
In[8]:=ab2 \times 3cd+xy-2z \\ \\
Out[8]=6abcd+xy-2 z](/sites/default/files/tex_cache/0a0841bc8fda5e6dc8a897bbc7490111.png)
Mathematica различает строчные (маленькие) и прописные (заглавные, большие) буквы
Встроенные функции и символы всегда начинаются с прописной буквы, поэтому пользовательские символы и выражения рекомендуется начинать со строчных букв.
Примеры встроенных символов:
![\tt
In[9]:= Pi \\
\phantom{In[9]:= }E \\
\phantom{In[9]:= }I \\ \\
Out[9]= $\pi$ \\ \\ \tt
Out[10]= $e$ \\ \\
Out[11]= $i$](/sites/default/files/tex_cache/4f3f52949ce95d8f33ce1d5d0a1081d4.png)
Чтобы вывести соответствующее десятичное представление для выражения 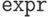 , нужно выполнить команду
, нужно выполнить команду ![\text{\tt N[expr]}](/sites/default/files/tex_cache/ca0b91dcf549dd0213a07b350736a06d.png) или
или ![\text{\tt N[expr,n]}](/sites/default/files/tex_cache/ffa8391ea85d764f26ecbadf8c58b534.png) , где
, где  - число цифр в десятичном представлении, например:
- число цифр в десятичном представлении, например:
![\tt
In[12]:=N[Pi] \\
\phantom{In[12]:=}N[Pi,10] \\
\phantom{In[12]:=}N[100Pi, 10] \\
\phantom{In[12]:=}N[E] \\
\phantom{In[12]:=}N[I] \\ \\
Out[12]=3.14159 \\ \\
Out[13]=3.141592654 \\ \\
Out[14]=314.1592654 \\ \\
Out[15]=2.71828 \\ \\
Out[16]=0.+1.i](/sites/default/files/tex_cache/bbb2df3bd9cf8b6bde115818653edaa0.png)
Присвоение значений командой Set или "=" (создание правила замены символа на присвоенное значение) и снятие присвоений командой Unset или "=."
![\tt
In[17]:=x=2 \\ \\
Out[17]=2 \\ \\
In[18]:= x \\ \\
Out[18]=2 \\ \\
In[19]:=x=. \\ \\
In[20]:= x \\ \\
Out[20]=x](/sites/default/files/tex_cache/ae7b7e6d89378487c33088c864026950.png)
Встроенным символам значения переприсвоить нельзя:
![\tt
In[21]:=Pi=10 \\ \\
\phantom{In[21]:}Set::wrsym: Symbol $\pi$ is Protected.>> \\ \\
Out[21]=10 \\ \\
In[22]:=Pi \\
\phantom{In[22]:=}N[Pi] \\ \\
Out[22]=$\pi$ \\ \\
Out[23]=3.14159 \\ \\
In[24]:=Pi=. \\ \\
\phantom{In[21]:}Unset::wrsym:Symbol $\pi$ is Protected.>> \\ \\
Out[24]=\$Failed \\ \\
In[25]:=Pi \\
\phantom{In[25]:=}N[Pi] \\ \\
Out[25]=$\pi$ \\ \\
Out[26]=3.14159](/sites/default/files/tex_cache/980d58257575575353f8e471b390d28f.png)
