Практикум по компьютерной геометрии
[+]
Опубликован: 27.12.2010 | Доступ: свободный | Студентов: 1030 / 278 | Оценка: 5.00 / 5.00 | Длительность: 18:38:00
ISBN: 978-5-9556-0117-5
Темы: Математика, САПР
Специальности: Математик
Теги: алгебра, анализ, вычисления, геометрия, программное обеспечение
Лекция 1:

Первое знакомство с пакетом Mathematica
A
|
версия для печати
Лекция 1: 123456789 || Лекция 2 >
Оператор While[test, body] выполняет body до тех пор, пока test дает True

Здесь \text{\tt n++} означает увеличение \text{\tt n} на единичку; равносильно \text{\tt n = n + 1}:

\tt In[179]:=n=1; m=1; While[n $\le$ 5, m=mn; n++; Print[m]] \\ \\ \phantom{In[179]}1 \\ \\ \phantom{In[179]}2 \\ \\ \phantom{In[179]}6 \\ \\ \phantom{In[179]}24 \\ \\ \phantom{In[179]}120
Оператор For[start, test, incr, body] выполняет start, затем последовательно выполняет body и incr до тех пор, пока test дает True:
\tt In[180]:= For[i=1; t=x, i\^\,\!2 < 10, i++, t=t\^\,\!3+I; Print[t]]} \\ \\ \phantom{In[180]}$1+x^3$ \\ \\ \phantom{In[180]}$2+\left(1+x^3\right)^3$ \\ \\ \phantom{In[180]}$3+\left(2+\left(1+x^3\right)^3\right)^3$
  • \text{\tt Break[]} выходит из ближайшего цикла;
  • \text{\tt Continue[]} переходит к следующему шагу в текущем цикле;
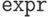  • \text{\tt Return[expr]} возвращает значение \text{\tt expr}, выходя при этом из всех процедур и циклов функции;
  • \text{\tt Goto[name]} переходит к элементу \text{\tt Label[name]} в текущей процедуре (в примере оператор \text{\tt t *= k} равносилен 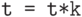\text{\tt t = t*k}):
\tt In[181]:=t=1;Do[t*=k; Print[t]; If[t > 19, Break[]],{k,10}] \\ \\ \phantom{In[181]:}1 \\ \\ \phantom{In[181]:}2 \\ \\ \phantom{In[181]:}6 \\ \\ \phantom{In[181]:}24

В следующем примере \text{\tt PrimeQ[n]} дает \text{\tt True}, если \text{\tt n} - простое число:

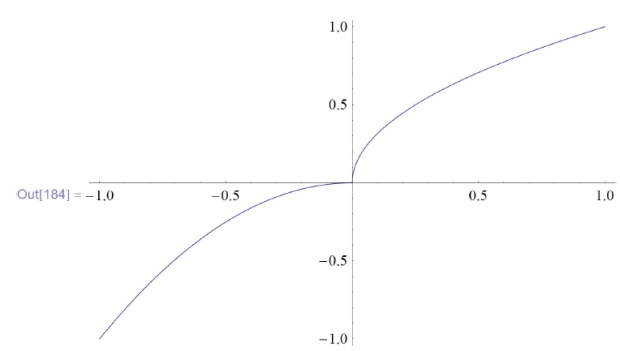
\tt In[182]:=Do[If[!PrimeQ[k], Continue[], Print[k]],{k, 15}] \\ \\ \phantom{In[182]:}2 \\ \\ \phantom{In[182]:}3 \\ \\ \phantom{In[182]:}5 \\ \\ \phantom{In[182]:}7 \\ \\ \phantom{In[182]:}11 \\ \\ \phantom{In[182]:}13 \\ \\ In[183]:=f[x\_]:=(If[x < 0, Return[-$x^2$]]; $x^2$) \\ \phantom{In[183]:=}Plot[f[x], {x, -1,1}]

\tt In[185]:=x=2; Label[start]; Print[x];x+=2;\\ \phantom{In[185]:=}If[x < 8, Goto[start]] \\ \\ \phantom{In[185]:}2 \phantom{In[185]:}4 \phantom{In[185]:}6 In[186]:= Clear[abs, abs1,a,res,I,m,n,t,f,x]
Последовательности команд. Локализация переменных

Как при определении выражений, так и в полях, отведенных для аргументов, можно писать не одно выражение, а последовательности выражений. Ниже приведены правила написания таких последовательностей

  1. Выражения последовательности разделяются точкой с запятой ";".
  2. Если после последнего выражения нет ";" , то результат вычисления этого последнего выражения выводится (например, в случае, когда последовательность введена в том месте, где должен стоять аргумент, значение присваивается аргументу). Если после последнего выражения стоит ";", то результат не выводится.
  3. При задании последовательности выражений, которую нужно присвоить некоторому выражению, или при задании безымянных функций эта последовательность берется в круглые скобки:
\tt In[187]:=For[ \\ \phantom{In[187]:=F}i=1; j=1, \\ \phantom{In[187]:=F}i+j $\le$ 10, \\ \phantom{In[187]:=F}i++, \\ \phantom{In[187]:=F}If[PrimeQ[i] \&\& PrimeQ[j] \&\& i $\le$ j, Primt[\{I,j\}]]; \\ \phantom{In[187]:=F}If[j < 9 \&\& i+j==10, j++; i=1] \\ \phantom{In[187]:=}] \\ \\ \phantom{In[187]:}\{2,2\} \\ \\ \phantom{In[187]:}\{2,3\} \\ \\ \phantom{In[187]:}\{3,3\} \\ \\ \phantom{In[187]:}\{2,5\} \\ \\ \phantom{In[187]:}\{3,5\} \\ \\ \phantom{In[187]:}\{5,5\} \\ \\ \phantom{In[187]:}\{2,7\} \\ \\ \phantom{In[187]:}\{3,7\}
In[188]:=f[y\_] := (If[y > 0, x="+"]; If[y < 0, x="\--"]; \\ \phantom{In[188]:=f[}If[y==0, x="!"];x) \\ \phantom{In[188]:=f}f[2] \\ \\ Out[189]=+ \\ \\ In[190]:=g[y\_] := (If[y > 0, x="+"]; If[y < 0, x="\--"]; \\ \phantom{In[190]:=g[}If[y==0, x="!"];x;) \\ \phantom{In[190]:=}g[2] \\ \\ In[192]:= \\ \phantom{In}Map[(If[\# > 0, x="+"]; If[\# < 0,x"\--"]; If[\#==0,x="!"]; \\ \phantom{In[192]}x)\&,\{1,-1,0\}] \\ \\ Out[192]=\{+,-,!\} \\ \\ In[193]:= \\ \phantom{In}Map[(If[\#>0,x="+"]; If[\# < 0,x"\--"]; If[\#==0,x="!"]; \\ \phantom{In[193]}x;)\& \{1,-1,0\}] \\ \\ Out[193]=\{Null, Null, Null\} \\ \\ In[194]:= Clear[I,j,x,f,g]

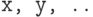В выражении \text{\tt Module[x,y, ..., expr]} переменные \text{\tt x, y, ..}. локальны, т. е. определены лишь внутри этой конструкции. При этом значения одноименных переменных, определенных снаружи, не используются при вычислении модуля, в то время как значения неодноименных наружных переменных используются.

Из приведенного примера видно, что внутренняя переменная 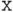\text{\tt x} на самом деле имеет другое имя:

\tt In[195]:=x=1; \\ \phantom{In[195]:=}y=2; \\ \phantom{In[195]:=}z=3; \\ \phantom{In[195]:=}Module[{x},x] \\ \phantom{In[195]:=}Module[{x}, x=5;z=6;xy] \\ \phantom{In[195]:=}x \\ \phantom{In[195]:=}z \\ \\ Out[198]=x\$1424 \\ \\ Out[199]=10 \\ \\ Out[200]=1 \\ \\ Out[201]=6

Локальным переменным можно присваивать начальные значения прямо в месте их декларации, т. е. \text{\tt Module[\{x = x0, y = y0, z, \ldots\}, expr]} (\text{\tt AxesOrigin} в команде \text{\tt Plot} задает координаты точки, через которую проводятся координатные оси):

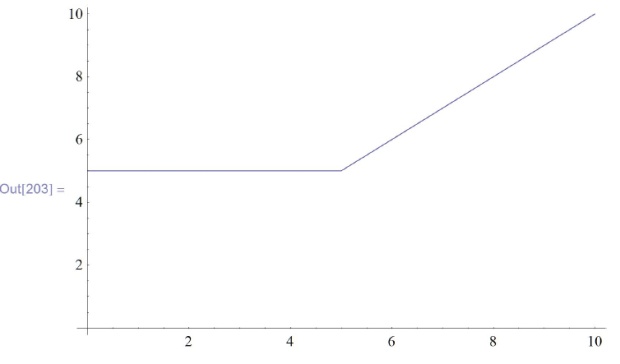
\tt In[202]:=\!f[x0\_]:= \\ \phantom{In[202]:=f[}Module[\{x=x0, y=5, z\}, z=y-x; If[z \ge 0,5,x] \\ \phantom{In[202]:=f[}]; \\ \phantom{In[202]:=}Plot[f[x],\{x,0,10\}, AxesOrigin \to \{0,0\}]

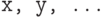Выражение \text{\tt Block[x, y, ..., expr]} вычисляется со значениями переменных \text{\tt x, y, ...}, заданных внутри блока. При этом значения одноименных переменных, определенных снаружи, используются при вычислении модуля, если они не были переопределены в блоке. Переопределенные в блоке переменные 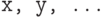\text{\tt x, y, ...} при выходе из блока восстанавливают свое предыдущее значение:

\tt In[204]:=x=2; \\ \phantom{In[204]:=}Block[{x},x] \\ \phantom{In[204]:=}Block[{x=5},x] \\ \phantom{In[204]:=}x \\ \\ Out[205]=2 \\ \\ Out[206]=5 \\ \\ Out[207]=2 \\ \\ In[208]:= Clear[x,y,z,f]
Дальше >>
Лекция 1: 123456789 || Лекция 2 >

Вопросы и ответы

вопросов: 0