Кривые и поверхности в компьютерной геометрии, II
Измельчение сетки при сохранении поверхности Безье
Добавление новых узлов в сетку Безье без изменения самой поверхности происходит по формулам, полностью аналогичным формулам добавления опорных точек в кривую Безье. Если дана сетка Безье 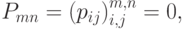 то увеличенная на одну строку и на один столбец сетка
то увеличенная на одну строку и на один столбец сетка 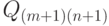 для той же самой поверхности Безье строится по формулам
для той же самой поверхности Безье строится по формулам
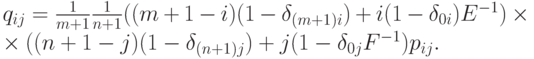
При этом углы новой сетки совпадут с углами старой: 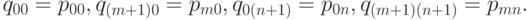
Вычисление дифференциально-геометрических характеристик поверхности Безье в произвольной точке
Прежде всего заметим, что с помощью деления поверхности Безье любая наперед заданная точка этой поверхности может быть представлена как угловая точка новой поверхности Безье, являющейся частью исходной, а потому имеющей в каждой своей точке те же самые дифференциально-геометрические свойства, что и исходная поверхность Безье. Следовательно, для вычисления дифференциально-геометрических характеристик поверхности Безье в произвольной точке достаточно уметь вычислять эти характеристики лишь для угловой точки поверхности Безье с нулевыми значениями параметрических координат.
Таким образом, достаточны следующие формулы.
Касательные векторы к поверхности Безье в угловой точке  могут быть вычислены по формулам
могут быть вычислены по формулам  и
и 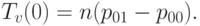
Нормаль к поверхности в угловой точке дается формулой 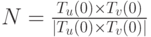
Вторые производные радиус-вектора поверхности Безье по параметрическим координатам в точке  равны
равны
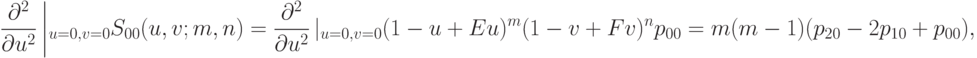
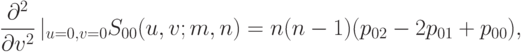
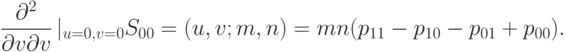
Вычислив, согласно приведенным формулам, первые и вторые производные в угловой точке, а также нормаль к поверхности в этой точке, мы сможем вычислить гауссову и среднюю кривизны, главные направления и главные кривизны в угловой точке. Все эти величины будут выражаться через узлы сетки: 
Для произвольной точки 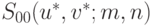 поступаем так:
поступаем так:
- делим поверхность в этой точке и вычисляем узлы
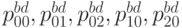 ;
; - вычисляем геометрические характеристики в данной точке через эти узлы.
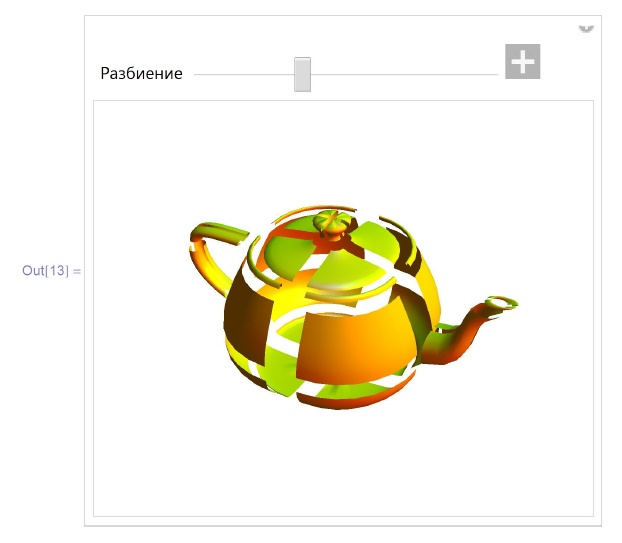
Пример 6.2.2. Чайник, нарисованный с помощью поверхности Безье. Чайник состоит из заплат:
In[13]:=
DynamicModule[{potPoints, рр2, potPatches, t, i, n, Bernstein,
BezierSurface}, potPoints = {{1.4, 0, 2.4},
(* Оставшиеся 304 точки *)
{1.425, -0.798, 0}}; (* это точки каркаса чайника, их 306 *)
рр2 = With[{avg = Mean [potPoints]}, Map[(j" - avg) &, potPoints]];
(*усреднили все точки и составили из них список*)
potPatches = {{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16},
(* оставшиеся тридцать заплат *)
{270, 270, 270, 270, 300, 305, 306, 279, 297, 303, 304, 275, 294,
301, 302, 271}}; ("чайник сосотоит из заплат, их 32 штуки*)
Bernstein [i_Tnteger, n_Integer, t_Symbol] : =
Binomial [n, i] t^i (1 - t) ^ (n - i) ; ("полиномы Бернштейна*)
Bernstein [n_Integer, t_Symbol] := Map [Bernstein [#, n, t] &, Range [0, n] ] ];
(*базис -- список всех полиномов Бернштейна*)
BezierSurface[pts_, u_, y_, m_] :=
Module [{dim = Dimensions [pts] , avg = Mean [Flatten [pts, 1]]},
Bernstein [dim[ [1] ] - 1, u] .Map [Bernstein [dim [ [2] ] - 1, v] .# &,
Map[(#) &, pts]] + m*avg] ; ("формула поверхности Безье*)
Manipulate[
ParametricPlot3D [Evaluate [BezierSurface [#, s, t, m] & / @
(Transpose [Partition [Part [pp2 , #] , 4]] & /@ potPatches) ] ,
(*делаем матрицу опорных точек и для них рисуем поверхность Безье*)
{s, 0, 1}, {t, 0, 1}, Axes -> None, Boxed -> False, Evaluated -> False,
PlotPoints -> ControlActive[{3, 3}, {8, 8}],
PlotStyle -> Directive[Specularity[White, 50], Yellow],
MaxRecursion -> 0, Mesh -> None, PerformanceGoal -> "Speed",
ImageSize -> {450, 350}], {{m, 0, "Разбиение"}, 0, 1},
SaveDefinitions -> True]]B-поверхности
Пусть задана матрица опорных точек 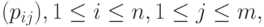 с весами (
с весами ( 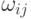 ). Фиксируем числа
). Фиксируем числа  и
и  - порядки B -сплайнов в двух координатных направлениях u и v соответственно. Тогда B -поверхность порядка (p,q), построенная по матрице опорных точек
- порядки B -сплайнов в двух координатных направлениях u и v соответственно. Тогда B -поверхность порядка (p,q), построенная по матрице опорных точек 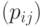 с весами
с весами 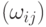 и по двум расширенным множествам узлов в направлениях u и v соответственно, определяется формулой
и по двум расширенным множествам узлов в направлениях u и v соответственно, определяется формулой
 |
( 6.11) |
Если ввести новые обозначения для входящих в эту формулу произведений B -сплайнов
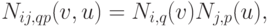
то формула (6.11) перепишется в виде
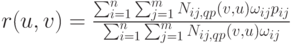 |
( 6.12) |
Если расширенные множества узлов в u и v -направлениях имеют вид
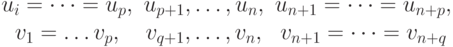
то область изменения параметров (u,v) на B -поверхности (6.12) будет следующей:
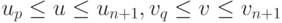
Задача 6.2.2. Наглядно изучить влияние опорных точек и расширенного множества узлов на B-поверхность, порождаемую пакетом Mathematica с помощью следующей программы. Поменять в программе автоматический выбор расширенных множеств узлов на прямое задание этих узлов. Изучить влияние расширенных множеств узлов на B -поверхность.
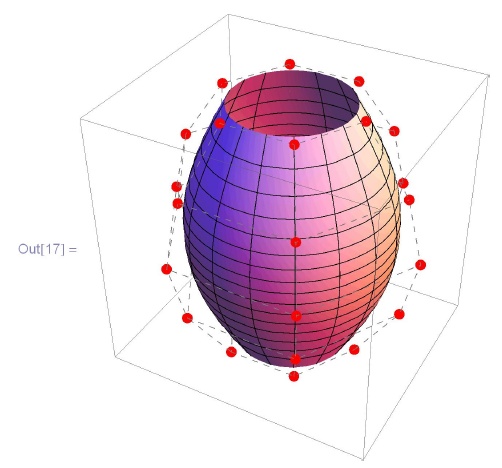
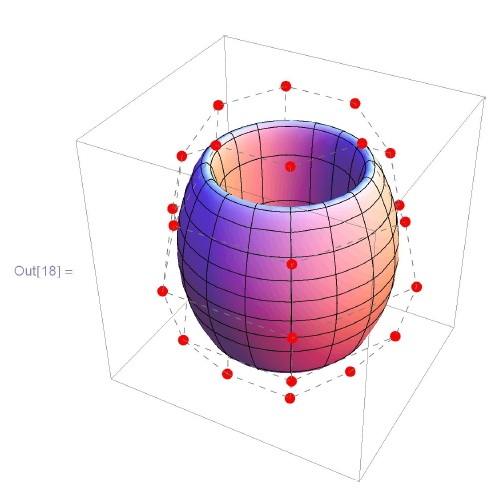
Пример 6.2.3. B -поверхность. Для обеих поверхностей задан одинаковый остов. В первом случае поверхность "замыкается" только по оси Ox, во втором случаем - по обеим осям.
In[14] : = pts = Table [{Cos [2 Pi u / 6] Cos [v] , Sin [2 Pi u / 6] Cos [v] , v} , {u, 6} ,
{v, -1, 1, 1/2}] ;
f = BSplineEunction [pts , SplineClosed -> {True, False},
SplineKnots -> Automatic] ;
g = BSplineFunction [pts , SplineClosed -> {True, True},
SplineKnots -> Automatic] ;
Show[Graphics3D[{PointSize[Large], Red, Map[Point, pts]}],
Graphics3D[{Gray, Dashed, Line[pts], Gray, Line[Transpose[pts]]}],
ParametricPlot3D[f [u, v] , {u, 0, 1}, {v, 0, 1}]]
Show[Graphics3D[{PointSize[Large], Red, Map[Point, pts]}],
Graphics3D[{Gray, Dashed, Line[pts], Gray, Line[Transpose[pts]]}],
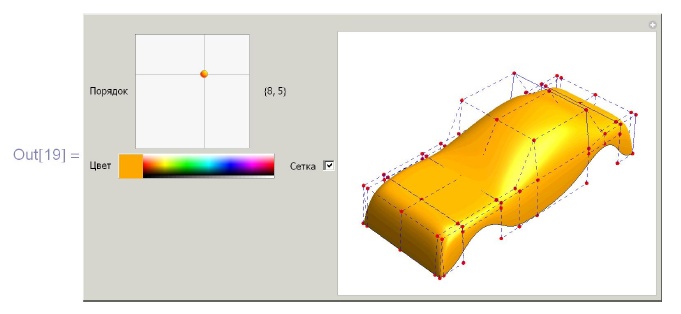
ParametricPlot3D[g[u, v] , {u, 0, 1} , {v, 0, 1}]]Пример 6.2.4. Моделирование кузова автомобиля с помощью В -поверхности.
In[19]: =
DynamicModule[{colour, carbody, deg, mesh},
Manipulate [Graphics3D [ {colour, Specularity [White, 50],
BSplineSurface[carbody, SplineDegree -> Floor[deg]],
If[mesh,
{Dashed, Blue, Line[carbody], Line[Transpose[carbody]],
Red, PointSize [Medium] , Point /@ carbody}, {}]},
Boxed -> False, Lighting -> "Neutral", RotationAction -> "Clip",
Viewpoint -> {-2, -2, 2}],
Row[
{Control[{{deg, {1, 1}, "Порядок"}, {1, 1}, {14, 7},
ImageSize -> {140, 140}}], Dynamic[Floor[deg]]}, Spacer[10]],
Row[
{Control[{{colour, Yellow, "Цвет"}, ColorData["HTML", "GoldenRod"]}],
Control[{{mesh, True, "Сетка"}, {False, True}}]}, Spacer[10]]],
Initialization :->
(carbody =
{{{-.2, -2.25, 0}, {-.2, -2.25, 0}, {-.2, -2, 0}, {-.2, 0, 0},
{-.2, 2, 0}, {-.2, 2.25, 0}, {-.2, 2.25, 0}}
(* Другие опорные точки *)
{{11, -2.25, 0}, {11, -2.25, 2}, {11, -2, 2}, {11, 0, 2},
{11, 2, 2}, {11, 2.25, 2}, {11, 2.25, 0}},
{{11.01, -2.25, 0}, {11.01, -2.25, 0}, {11.01, -2, 0},
{11.01, 0, 0}, {11.01, 2, 0}, {11.01, 2.25, 0}, {11.01, 2.25, 0}}
})]Пример 6.2.5. Интерполяция заданного рисунка с помощью поверхности Безье и B -поверхности.
In[20]: =
DynamicModule {f, colfun, prevn =5, prevapprox =True, start, locators, grid,
order, approx, images},Manipulate {* Создали список, который задает рисунок,
и для этого списка построили В-функцию, т.е. мы "синтерполировали" рисунок*)
colfun = BSplineFunction[ImageDatafimages[[ii]]] , SplineDegree ->1] ;
(* Первоначальная сетка *)
If [n = ! = prevn ,
pts = Flatten [Table [{i, j}, {i, 0, 1, 1/ (n - 1) }, {j , 0, 1, 1 / {n- 1) }] , 1] ;
If[approx, order = n - 1, order = 2] ; prevn = n];
(* Выбираем порядок интерполяции *)
If [ approx = ! = prevapprox, If [ approx, order = n - 1, order = 2 ] ; prevapprox = approx] ;
If[approx,
f = BSplineFunction [Partition [pts , n] , SplineDegree -> order,
Method -> {"Extrapolation" -> "Clamp"1}] ,
f = Interpolation[
Flatten[Table[{{N[1 / (n-1)] i, N[1/ (n-1)] j } , pts [ [nit] + 1] ] } ,
{i, 0, n-1}, {j, 0, n-1}], 1], Method -> "Spline" , InterpolationOrder -> order] ]
];
{*Рисуем картинки*)
ParametricPlot[f [u, v] , {u, 0, 1}, {v, 0, 1}, ColorFunction -> (colfun [1 - #4, #3] &) ,
MaxRecursion -> 0, PlotPoints -> ControlActive[20, 100] , Mesh -> None,
Epilog ->
{If[grid, {Gray, Opacity[,7], Line[Partition[pts, n] ] ,
Line[Transpose[Partition[pts, n]]]}, {}], If[locators, Locator/@pts, {}]},
ImageSise -> 400, PlotRange -> { {0 , 1}, {0, 1}}, PlotRangePadding -> Scaled[. 03] ,
FrameTicks -> None] ,
(*элементы управления*)
{{pts, Flatten[Table[{i, j}, {i, 0, 1, .25}, {j, 0, 1, -25}], 1]}, {0, 0},
{1, 1}, Locator, Appearance -> None} ,
{{ii, 1, "Объкт интерполирования"}, {1 -> ''Медведь" , 2 -> "Шахматная доска"},
ControlType -> RadioButton} ,
Delimiter, {{n, 4, "Размер сетки"}, 4, 8, 1, ControlType -> RadioButton} ,
{{approx, True, ''Метод"}, {True -> "Поверхность Безье" , False -> "В-поверхность" } ,
ControlType -> RadioButton} ,
{{order, 3, "Порядок В-поверхности"},
Dynamic [RadioButtonBar [Dynamic [order] , Range [2, n-1, 1],
Enabled -> Not [ approx ] ] ] & } ,
Delimiter, Row[{Control[{{grid, True, "Показать сетку"}, {True, False}}],
Control[{{locators, True, "Показать локаторы"}, {True, False}}],
Control[{{start, " ", " "},
Button["Первоначальная сетка",
pts = Flatten [Table[{i, j} , {i, 0, 1, l/(n-l)}, {j, 0, 1, l/(n-l)}], 1]] &}]},
Spacer[10]],
{* Код, соответствующий второму рисунку,
следующий:
Image[Table[Boole[Xor[EvenQ[Quotient[i-1,20]],EvenQ[Quotient[j-1,20]]]],
{i,200},{j,200},{k,3}]] *)
Initialization:-> ( images = {};) ]]