Графика: основные принципы
Графика, порожденная функциями и другими числовыми данными
Двумерная графика
Как уже говорилось в начале,  располагает специальным арсеналом средств, позволяющих визуализировать числовые данные и функции. Самый простой и известный способ визуализировать функцию - это построить ее график. Это делается с помощью уже встречавшейся нам команды
располагает специальным арсеналом средств, позволяющих визуализировать числовые данные и функции. Самый простой и известный способ визуализировать функцию - это построить ее график. Это делается с помощью уже встречавшейся нам команды  :
:
![\tt
In[61]:=Plot[Sin[x], \{х, -$\pi$, $\pi$\}]](/sites/default/files/tex_cache/c1ef84f14422316ecb7f416f27202045.png)
На самом деле команда  генерирует по данной функции графические примитивы, директивы и опции и формирует затем соответствующую команду
генерирует по данной функции графические примитивы, директивы и опции и формирует затем соответствующую команду  :
:
![\tt
In[62]:=InputForm[Plot[Sin[x], \{x, -$\pi$, $\pi$\}]] //Short \\ \\
Out[62]=Graphics[\{\{\{\}, \{\}, \{Hue[0.67, 0.6,\\
\phantom{Out[62]=Gr}0.6], Line[\{\{<<2>>, <<30>>\}]\}\}\}, \{<<6>>\}]](/sites/default/files/tex_cache/ac71a76590e817b1ce25b8db9bfa6529.png)
Таким образом, мы видим, что  , на самом деле, строит ломаную линию. При желании этим можно воспользоваться:
, на самом деле, строит ломаную линию. При желании этим можно воспользоваться:
![\tt
In[63]:=gg = Plot[Sin[x], \{х, -$\pi$ ,$\pi$\}];\\
\phantom{In[63]:=}gg[\!\![l, 1, 3, 1]\!\!]\\ \\
Out[64]=Hue[0.67, 0.6, 0.6]](/sites/default/files/tex_cache/89dee6d8d4ae964be074f00af810f4cf.png)
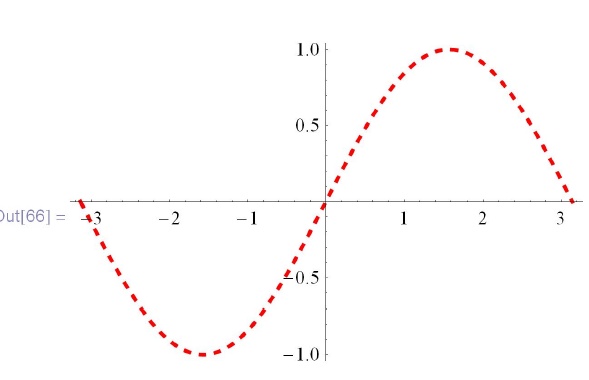
Вот мы вычленили директиву, предшествующую собственно ломаной. Ее можно подменить, например так:
![\tt
In[65]:=gg[\!\![l, 1, 3, l]\!\!] = Sequence [Red, Thick, Dashed];\\
\phantom{In[65]:=}gg](/sites/default/files/tex_cache/5c1f3ec22c23977c18656f2f87087ccc.png)
С одной стороны, в командах типа  можно использовать опции обычной графики. С другой стороны, есть и специальные способы управления, главные из которых
можно использовать опции обычной графики. С другой стороны, есть и специальные способы управления, главные из которых  и
и  . Опция
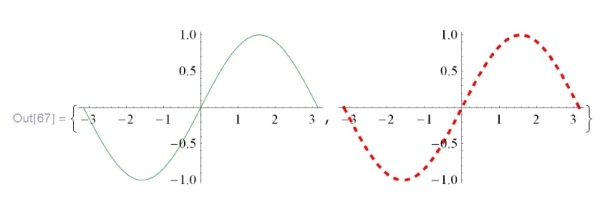
. Опция  служит для использования уже знакомых нам графических директив. Теперь
служит для использования уже знакомых нам графических директив. Теперь  сама поставит их в нужное место в команде
сама поставит их в нужное место в команде  :
:
![\tt
In[67]:=\{Plot[\{Red, Dashed, Thick, Sin[x]\}, \{x, -$\pi$, $\pi$\}],\\
\phantom{In[67]:=\{}Plot[Sin[x], \{x, -$\pi$, $\pi$\},\\
\phantom{In[67]:=\{P}PlotStyle $\to$ \{RGBColor[l, 0, 0], Dashed, Thick\}]\}](/sites/default/files/tex_cache/7dfbb6bec238cb96e51749af1f2edacc.png)
Опция  служит для управления цветом изображаемого графика. Имена и смысл переменных этой функции фиксированы (для каждого типа графики - свои, для обычного
служит для управления цветом изображаемого графика. Имена и смысл переменных этой функции фиксированы (для каждого типа графики - свои, для обычного  , например, это
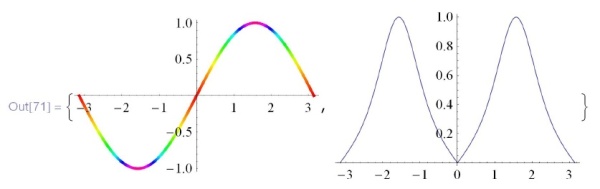
, например, это 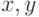 ). В качестве примера раскрасим график в соответствии с кривизной соответствующей плоской кривой:
). В качестве примера раскрасим график в соответствии с кривизной соответствующей плоской кривой:
![\tt
In[68]:=ClearAll[g];\\
\phantom{In[68]:=}cur[f\_][t\_] := $\frac{Abs[D[f[t],t,t]]}{(l+D[f[t],t]^2)^{3/2}}$;\\
\phantom{In[68]:=}g[t\_] = cur[Sin][t]; \\
\phantom{In[68]:=}\{Plot[Sin[x], {x, -$\pi$, $\pi$\}, PlotStyle $\to$ \{Thick\},\\
\phantom{In[68]:=Cl}ColorFunction $\to$ Function [\{x, y\}, Hue$[\frac{g[x]}{1.1}]$],\\
\phantom{In[68]:=Cl}ColorFunctionScaling $\to$ False],\\
\phantom{In[68]:=C}Plot[g[t], \{t, -$\pi$, $\pi$\}]\}](/sites/default/files/tex_cache/7b8a25329c5ec93d0b75d1a7da61355b.png)
Замечание. На самом деле, чтобы картина была реалистичной, пришлось отмасштабировать кривизну так, чтобы она менялась от 0 до 1/2 (важно, чтобы не доходила до 1). Здесь мы пользуемся тем, что кривизна графика синуса меняется от нуля (на рисунке - красный) до единицы (синий). Опция  отключает автоматическое масштабирование функции, отвечающей за цвет, которое затемняет дело.
отключает автоматическое масштабирование функции, отвечающей за цвет, которое затемняет дело.
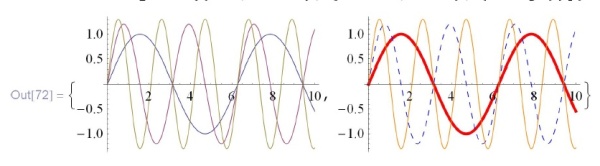
Перечислим теперь встроенные возможности функции  . Во-первых, можно рисовать сразу несколько графиков, причем они автоматически получаются разноцветными. Можно и самим регулировать их вид (с помощью
. Во-первых, можно рисовать сразу несколько графиков, причем они автоматически получаются разноцветными. Можно и самим регулировать их вид (с помощью  ):
):
![\tt
In[72]:=\{Plot[\{Sin[x], 1.2Sin[2x], 1.3Sin[3x]\}, \{x, 0, 10\}],\\
\phantom{In[72]:=\{}Plot[\{Sin[х], 1.2Sin[2x], 1.3Sin[3x]\}, \{x, 0, 10\},\\
\phantom{In[72]:=\{P}PlotStyle $\to$ \{\{Red, Thick\}, \{Dashed, Blue\}, \{Orange\}\}]\}](/sites/default/files/tex_cache/df93e626cd5b12d37709b88b40bfc3e7.png)
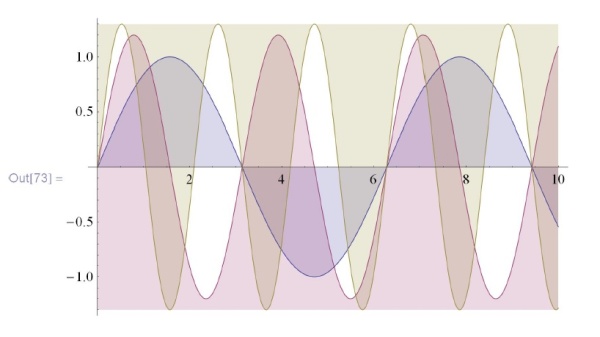
Можно также закрашивать области, ограниченные графиком (графиками). Это исполняется с помощью опции  , значение которой устанавливается в тип заполнения ("до оси", "подграфик", "надграфик"):
, значение которой устанавливается в тип заполнения ("до оси", "подграфик", "надграфик"):
![\tt
In[73]:=Plot[\{Sin[x], 1.2Sin[2x], 1.3Sin[3x]\}, \{x, 0, 10\}, \\
\phantom{In[73]:=P}Filling $\to$ \{l $\to$ Axis, 2 $\to$ Bottom, 3 $\to$ Top\}]](/sites/default/files/tex_cache/d026a2b7097b5a4375e0be3a20a0cd16.png)
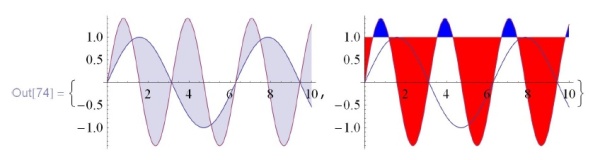
Более хитрый вид заполнения: для 2-го объекта выбрано заполнение до 1-го. Можно также добавить директивы, как именно заполнять:
![\tt
In[74]:=\\
\phantom{In}\{Plot[\{Sin[x], 1.4Sin[2x]\}, \{х, 0, 10\}, Fillings $\to$ \{2 $\to$ \{1\}\}],\\
\phantom{In\{}Plot[\{Sin[x], 1.4Sin[2x]\}, \{x, 0, 10\},\\
\phantom{In\{P}Filling $\to$ \{2 $\to$ \{l, \{Red, Blue\}\}\}]\}](/sites/default/files/tex_cache/01eca8155ea39e3cbdc88638e973a3bd.png)
Можно явно указать, сколько точек участвуют в построении ломаной, изображающей кривую. Современные версии  сами следят за качеством графика, поэтому
сами следят за качеством графика, поэтому  в двумерной графике - это начальное количество точек аппроксимации (по умолчанию равен 50). Если картинка
в двумерной графике - это начальное количество точек аппроксимации (по умолчанию равен 50). Если картинка  не нравится, она сама подразобьет кривую столько раз, сколько ей захочется. Чтобы запретить ей это, нужно ограничить рекурсию с помощью опции
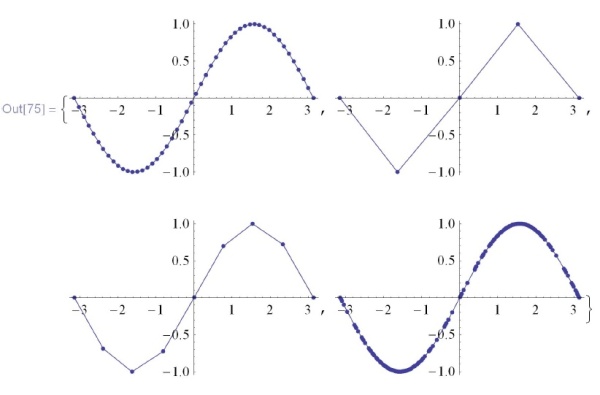
не нравится, она сама подразобьет кривую столько раз, сколько ей захочется. Чтобы запретить ей это, нужно ограничить рекурсию с помощью опции  (которая устанавливается в количество итераций). Чтобы увидеть точки-вершины ломаной, нужно использовать опцию
(которая устанавливается в количество итераций). Чтобы увидеть точки-вершины ломаной, нужно использовать опцию  :
:
![\tt
In[75]:=\{Plot[Sin[x], \{x, -$\pi$, $\pi$\}, Mesh$\to$All, MaxRecursion$\to$0],\\
\phantom{In[75]:=\{}Plot[Sin[x], \{x, -$\pi$, $\pi$\}, PlotPoints$\to$5, Mesh$\to$All,\\
\phantom{In[75]:=\{P}MaxRecursion$\to$0],\\
\phantom{In[75]:=\{}Plot[Sin[x], \{x, -$\pi$, $\pi$\}, PlotPoints$\to$5, Mesh$\to$All,\\
\phantom{In[75]:=\{P}MaxRecursion$\to$1],\\
\phantom{In[75]:=\{}Plot[Sin[x], \{x, -$\pi$, $\pi$\}, PlotPoints$\to$5, Mesh$\to$All]\}](/sites/default/files/tex_cache/b640068d082457adced7aa0e763afc72.png)
Иногда полезно исключить из рассмотрения какие-нибудь точки. Для этого служит опция  , которая устанавливается в условие:
, которая устанавливается в условие:
![\tt
In[76]:=\{Plot[Tan[x], \{х, -2$\pi$, 2$\pi$\}],\\
\phantom{In[76]:=\{}Plot[Tan[x], \{х, -2$\pi$, 2$\pi$\}, Exclusions$\to$\{Cos[x] == 0\}]\}](/sites/default/files/tex_cache/eba9e2932b99442d1cdd18401676d798.png)
К двумерным способам представления числовых данных относятся так же:
-
 ,
, -
 ,
, -
 ,
, -
 .
.
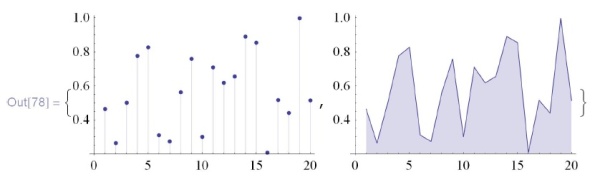
Первые три служат для изображения дискретных данных (одномерных или двумерных). Вот одномерные данные:
![\tt
In[77]:=data = Table [Random[], \{20\}];\\
\phantom{In[77]:=}\{ListPlot[data, Filling $\to$ Axis], \\
\phantom{In[77]:=d}ListLinePlot[data,Filling $\to$ Axis]}](/sites/default/files/tex_cache/b2edcce44e8e66cac4865070d14d6d5e.png)
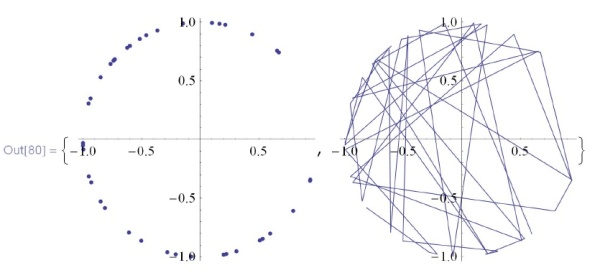
А вот - двумерные. Обратите внимание, что  просто соединяет последовательные точки линией.
просто соединяет последовательные точки линией.
![\tt
In[79]:=\\
\phantom{In}data = Table[\{Cos[\#], Sin[\#]\} \& [Random[Real, 2$\pi$]], \{i, 1, 40\}];\\
\phantom{In}\{ListPlot[data, AspectRatio $\to$ Automatic],\\
\phantom{Ind}ListLinePlot[data, AspectRatio $\to$ Automatic]\}](/sites/default/files/tex_cache/a80cb4745f1e0cc9877b4bc1c6b74f5e.png)
 изображает числа строки в виде раскрашенных квадратиков. По умолчанию они черно-белые, но можно их и раскрасить:
изображает числа строки в виде раскрашенных квадратиков. По умолчанию они черно-белые, но можно их и раскрасить:
![\tt In[81]:=ArrayPlot[Transpose[data]]](/sites/default/files/tex_cache/c1af0f770d6c5c3ce5b41590b634557c.png)
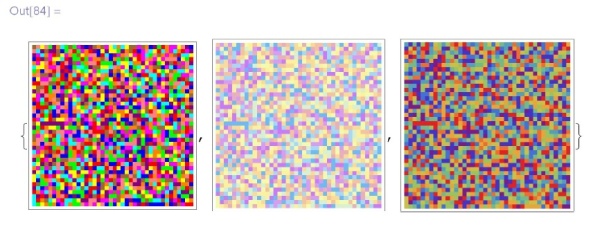
Можно задать цвета явно с помощью правил  , можно использовать
, можно использовать  . Мы нарисуем число
. Мы нарисуем число  :
:
![\tt
In[82]:=curpet[х\_, m\_, n\_] :=\\
\phantom{In[82]:=cu}Module[\{res, хх, i\},\\
\phantom{In[82]:=cur}(*Эта подпрограммка вычисляет цифры числа х и \\
\phantom{In[82]:=curp}организовывает их в массив\}*)\\
\phantom{In[82]:=cur}хх = N[x, m n];\\
\phantom{In[82]:=cur}res = \{RealDigits[хх, 10, m] [\!\![1]\!\!]\};\\
\phantom{In[82]:=cur}xx = xх/10$^{\text{RealDigits}[xx,10,m][\![2]\!]}$;\\
\phantom{In[82]:=cur}For[i = l, i $\le$ n - 1, i++,\\
\phantom{In[82]:=curp}res = res$\sim$Join$\sim$\{RealDigits[xx, 10, m, -m i - 1][\!\![1]\!\!]\}\\
\phantom{In[82]:=cur}];\\
\phantom{In[82]:=cur}res\\
\phantom{In[82]:=cu}];\\
\phantom{In[82]:=}rules = \{0$\to$Red, 1$\to$Pink, 2$\to$Orange, 3$\to$Brown, 4$\to$Yellow,\\
\phantom{In[82]:=cur}5$\to$Green, 6$\to$Cyan, 7$\to$Blue, 8$\to$Magenta, 9$\to$Purple\};](/sites/default/files/tex_cache/243c8c91f7a95b499077179c1f0d5c38.png)
![\tt
In[84]:={ArrayPlot[curpet[$\pi$, 40, 40], ColorRules$\to$rules],\\
\phantom{In[84]:=\{}ArrayPlot[curpet[$\pi$, 40, 40], ColorFunction$\to$"Pastel"\ \!\!\!],\\
\phantom{In[82]:=\{}ArrayPlot[curpet[$\pi$, 40, 40], ColorFunction$\to$"Rainbow"\ \!\!\!] \}](/sites/default/files/tex_cache/491999292f51d23f6afd0a766ee6e26b.png)
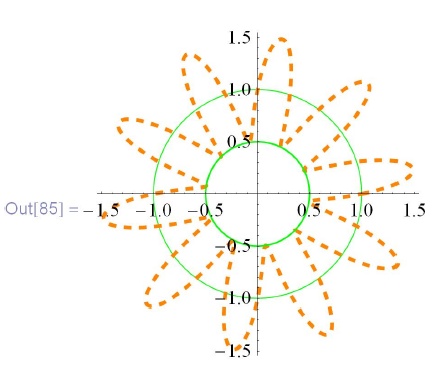
Команда  удобна для рисования кривых, заданных в полярных координатах. Имеется также ее модификация
удобна для рисования кривых, заданных в полярных координатах. Имеется также ее модификация  :
:
![\tt
In[85]:=PolarPlot[\{l, 1 + 1/2Sin[10t], 1/2\}, \{t, 0, 2Pi\},\\
\phantom{In[85]:=P}PlotStyle $\to$ \{Green, \{Dashed, Thick, Orange\},\\
\phantom{In[85]:=Pol}\{Thickness[0.005], Green\}\}]](/sites/default/files/tex_cache/7253fca544bdcfe6392e8a87a5c2f75b.png)