Графика: основные принципы
Директивы
Директивы непосредственного управления цветом
В  цвет задается разными способами. Кроме названий стандартных цветов и четырех основных оттенков серого (тут мы пользуемся упомянутым выше примитивом
цвет задается разными способами. Кроме названий стандартных цветов и четырех основных оттенков серого (тут мы пользуемся упомянутым выше примитивом  )
)
![\tt
In[27]:=\\
\phantom{In}colors = \{Red, Green, Blue, Cyan, Magenta, Yellow, Brown,\\
\phantom{Incol}Orange, Pink, Purple,\\
\phantom{Incol}LightRed, LightGreen, LightBlue, LightCyan, LightMagenta,\\
\phantom{Incol}LightYellow, LightBrown, LightOrange, LightPink,\\
\phantom{Incol}LightPurple\}; \\
\phantom{In}cl = Partition[Map[Apply[List, \#] &, colors], 10];\\
\phantom{In}Graphics[Raster[cl]]](/sites/default/files/tex_cache/eb00c3ff41bc7fb951a16d858fb8e5ce.png)
![In[30]:=Graphics[Raster[{Map[\#[\!\![1]\!\!] &, \{Black, White, Gray, LightGray\}]\}]]](/sites/default/files/tex_cache/2040bd4edb64efb04eeb10f1ace09a6c.png)
которыми мы уже пользовались выше, есть возможность задавать цвет в форматах  и, кроме того,
и, кроме того,  для оттенков серого. В первых двух результирующий цвет представлен как сумма монохромных слагаемых (
для оттенков серого. В первых двух результирующий цвет представлен как сумма монохромных слагаемых ( - красный,
- красный,  - зеленый,
- зеленый,  - синий) и (
- синий) и ( - голубой,
- голубой,  - фиолетовый,
- фиолетовый,  - желтый,
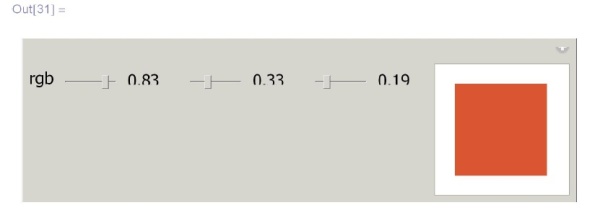
- желтый,  - черный), принимающих значения от нуля до единицы, что проиллюстрировано в следующих примерах:
- черный), принимающих значения от нуля до единицы, что проиллюстрировано в следующих примерах:
![\tt
In[31]:=
\phantom{In}Manipulate[\\
\phantom{InM}Graphics[\{RGBColor[r, g, b], Rectangle[\{0, 0\}, \{1, 1/3\}]\}],\\
\phantom{InM}\{r, 0, 1, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \},\\
\phantom{InM}\{g, 0, 1, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \},\\
\phantom{InM}\{b, 0, 1, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \}]](/sites/default/files/tex_cache/f025c33df1b099bc92269d3771995aef.png)
![\tt
In[32]:=\\
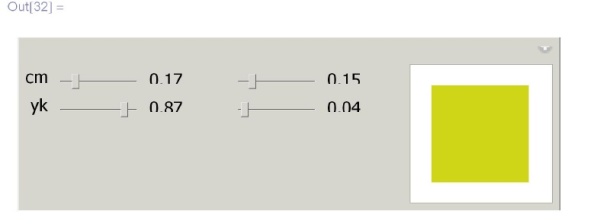
\phantom{In}Manipulate[\\
\phantom{InM}Graphics[\{CMYKColor[c, m, y, k], Rectangle [\{0, 0\}, \{1, 1/3\}]\}],\\
\phantom{InM}\{c, 0, 1, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \},\\
\phantom{InM}\{m, 0, 1, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \},\\
\phantom{InM}\{m, 0, 1, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \},\\
\phantom{InM}\{k, 0, 1, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \}]](/sites/default/files/tex_cache/ce5d75718a9d11c2e6eb05541c5aca6b.png)
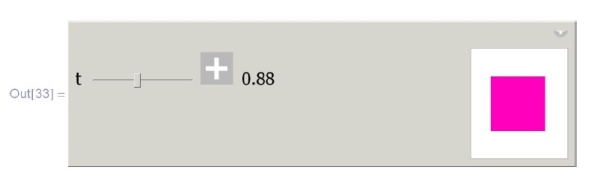
Управление с помощью функции  может быть как однопараметрическим (от красного к фиолетовому и обратно), так и трех- и четырех параметрическим (
может быть как однопараметрическим (от красного к фиолетовому и обратно), так и трех- и четырех параметрическим ( ):
):
![In[33]:=\\
\phantom{In}Manipulate[Graphics[\{Hue[t], Rectangle[\{0, 0\}, \{1, 1/3\}]\}],\\
\phantom{InM}\{t, 0, 2, Appearance $\to$ "Labeled"\ \!\!\!\!\!\! \}]](/sites/default/files/tex_cache/d61a865f43cd0e181d7dd86fd9655553.png)
![\tt
In[34]:=\\
\phantom{In}Craphics[Table[\{Hue[h], Edgeform[Gray], Rectangle[\{32h, 0\}]\},\\
\phantom{InGr}\{h, 0, 1, 1/32\}]]](/sites/default/files/tex_cache/915ba2b00c339d765412c70dd3346f54.png)
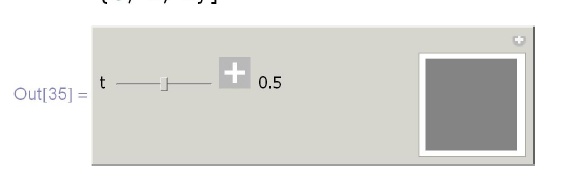
Также однопараметрически оттенки серого задаются с помощью функции  :
:
![\tt
In[35]:=Manipulate[\\
\phantom{In[35]:=M}Graphics[\{GrayLevel[t], Rectangle[\{0, 0\}, \{1, 1/3\}]\}],\\
\phantom{In[35]:=M}\{t, 0, 1\}]](/sites/default/files/tex_cache/aaf99dd9dc27d6a56c882b327e6a8459.png)
Директивы, управляющие размерами. Абсолютные и относительные характеристики
Pазмеры составляющих рисунок примитивов можно задавать как в абсолютных единицах, так и в относительных. Абсолютная единица размера точки равна 1/72 дюйма (т. е. та самая точка -  старого матричного принтера). Относительная единица - это доля от размера рисунка.
старого матричного принтера). Относительная единица - это доля от размера рисунка.
Размер точки
![\tt
In[36]:=Graphics[
\phantom{In[35]:=G}Table[\{Hue[1/i], AbsolutePointSize[i], Point[\{i,0\}]\},\\
\phantom{In[35]:=MT}\{i, 1, 20\}]]](/sites/default/files/tex_cache/ab6d3e784bce80b51f79423a7215ea2b.png)
![\tt
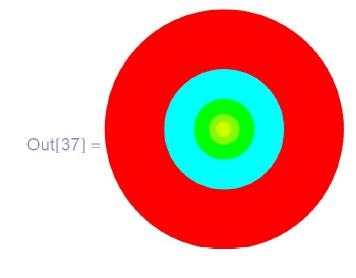
In[37]:=\\
\phantom{In}Graphics[Table[\{PointSize[1/2^{i-1}], Hue[1/i], Point[\{0, 0\}]\},\\
\phantom{InGr}\{i, 1, 5\}]]](/sites/default/files/tex_cache/432fa0fdd84aa82443317ada8e2b6440.png)
Сплошная или пунктирная линия, размер черточек и пробелов
Директива ![\text{\tt AbsoluteDashing[\{d1, d2, ..\}]}](/sites/default/files/tex_cache/3fff7759c0c7995befaacedf16b663a3.png) - последующие линии рисуются пунктиром с циклически повторяющимися интервалами абсолютных длин
- последующие линии рисуются пунктиром с циклически повторяющимися интервалами абсолютных длин  , видимо, в пикселях. Директива
, видимо, в пикселях. Директива ![\text{\tt Dashing[\{d1, d2, ..\}]}](/sites/default/files/tex_cache/724ea9f902c36dd7a6131470b3263a30.png) - то же, но размеры в долях ширины всей картинки.
- то же, но размеры в долях ширины всей картинки.
Чтобы почувствовать разницу между  и просто
и просто  , полезно поменять мышкой размер рисунка. При этом не меняется длина абсолютных
, полезно поменять мышкой размер рисунка. При этом не меняется длина абсолютных  -ей (большая окружность и отрезок, идущий вправо вверх) и количество относительных
-ей (большая окружность и отрезок, идущий вправо вверх) и количество относительных  -ей (все остальные линии).
-ей (все остальные линии).
![\tt
In[38]:=\\
\phantom{In}Graphics[\{AbsoluteDashing[\{1, 5, 10\}], Line[\{\{0, 0\}, \{1, 1\}\}],\\
\phantom{InGr}Circle[], Dashing[\{.1, .2\}], Line[\{\{0, 0\}, \{1, -1\}\}],\\
\phantom{InGr}Circle[\{0, 0\}, 1/2]\}]](/sites/default/files/tex_cache/43e4a16c25facc2ac700cb8e651098a0.png)
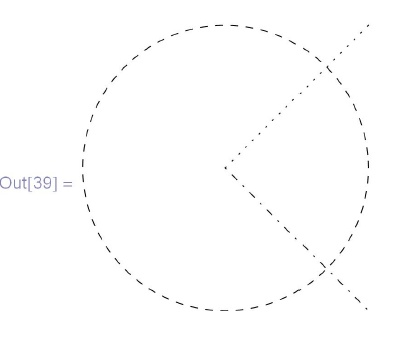
Возможны сокращенные версии этих абсолютных директив:  :
:
![\tt
In[39]:=\\
\phantom{In}Graphics[\{Dotted, Line[\{\{0, 0\}, \{1, 1\}\}], Dashed, Circle[],\\
\phantom{InGr}DotDashed, Line[\{\{0, 0\}, \{1, -1\}\}]\}]](/sites/default/files/tex_cache/7ad394b85a4727c3d2a4514fe9936946.png)
Толщина линии Аналогично, имеются команды, управляющие толщиной линии:
![\tt
In[40]:=AbsoluteThickness[r](*абсолютная толщина*) \\
\phantom{In[40]:=}Thickness[r](*относительная толщина*) \\
\phantom{In}Thin \\
\phantom{In}Thick \\ \\
Out[40]=AbsoluteThickness[r] \\ \\
Out[41]=Thickness[r] \\ \\
Out[42]=Thickness[Tiny] \\ \\
Out[43]=Thickness{Large] \\ \\
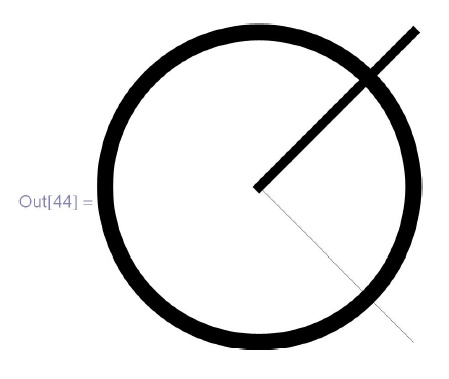
In[44]:= \\
\phantom{In}Graphics[{AbsoluteThickness[5], Line[\{\{0, 0\}, \{1, 1\}\}], \\
\phantom{In}Thickness[0.05], Circle[], Thin, Line[\{\{0, 0\}, \{1, -1\}\}]\}]](/sites/default/files/tex_cache/19ed6516f833c549f11690474eb95bcd.png)
Снова поменяйте мышкой размер рисунка. Толщина абсолютных линий не меняется. Относительные линии меняют абсолютную толщину вместе с рисунком.