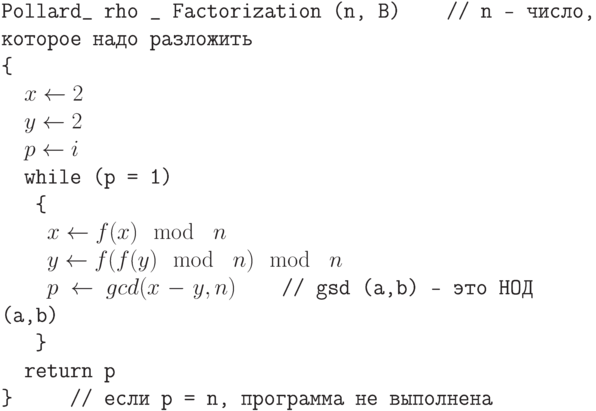|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Простые числа
РО (Rho) – метод Полларда
В 1975 г. Джон М. Поллард разработал второй метод для разложения на множители, который базируется на следующих положениях:
a. Предположим, что есть два целых числа, x1 и x2, таких, что p делит x1 – x2, но эта разность не делится на n.
b. Может быть доказано, что p = НОД (x1 – x2, n). Поскольку p делит x1 – x2 , можно записать, что 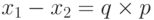 . Но поскольку n не делит x1 – x2, очевидно, что q не делится n. Это означает, что НОД (x1 – x2, n) является либо 1, либо сомножитель.
. Но поскольку n не делит x1 – x2, очевидно, что q не делится n. Это означает, что НОД (x1 – x2, n) является либо 1, либо сомножитель.
Следующий алгоритм повторно выбирает x1 и x2, пока не находит соответствующую пару.
- Выберите x1 — малое случайное целое число, называемое первоисточником.
- Используйте функцию, чтобы вычислить x2, такую, чтобы n не делило x1 – x2. Функция, которая может быть применена, — это x2 = f (x1 ) = x1 2 + a (a обычно выбирается как 1).
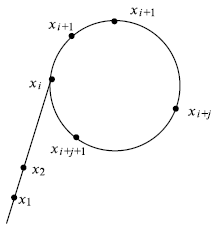
- Вычислить НОД (x1 – x2 , n). Если это не 1, результат – сомножитель. Алгоритм останавливается. Если это 1, то происходит возвращение, чтобы повторить процесс с x1. Теперь мы вычисляем x3. Заметим, что в следующем раунде мы начинаем с x3 и так далее. Если мы перечислим значения нескольких x, используя РО (rho) алгоритм Полларда, мы увидим, что дуга значений в конечном счете повторяется, создавая форму, подобную греческой букве РО (rho) или в греческом алфавите
 ), как это показано на рис. 12.2.
), как это показано на рис. 12.2.
Чтобы уменьшить число итераций, алгоритм был немного изменен. Он начинается с пары (x0, x0), и итеративно вычисляет (x1, x2), (x 2, x4), (x3, x6), …. (xi .x2i), используя равенство xi+1 = f (xi). В каждой итерации мы применяем функцию f (xi) (начиная с шага 2). При этом вычисление идут следующим образом: в паре вычисляется один раз первый элемент и дважды вычисляется второй элемент (см. алгоритм 12.6).
12.6. Алгоритм 12.6
Сложность. Метод требует 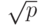 арифметических операций. Однако поскольку мы предполагаем, что p будет меньше или равняться
арифметических операций. Однако поскольку мы предполагаем, что p будет меньше или равняться 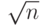 , мы ожидаем около n1/4 арифметические операций. Это означает, что сложность разрядной операции 0 (
, мы ожидаем около n1/4 арифметические операций. Это означает, что сложность разрядной операции 0 ( ) показательна.
) показательна.
Пример 12.32
Предположим, что есть компьютер, который, может выполнить 230 (почти 1 миллиард) разрядных операций в секунду. Какое приблизительно время потребуется, чтобы разложить на множители целое число размера
a. 60 десятичных цифр
b. 100 десятичных цифр
Решение
a. Множество 60 десятичных цифр имеют почти 200 битов. Сложность —  или 250. Со скоростью 230 операций в секунду алгоритм может быть выполнен в 220 секунды или почти за 12 дней
или 250. Со скоростью 230 операций в секунду алгоритм может быть выполнен в 220 секунды или почти за 12 дней
b. Множество 100 десятичных цифр — это почти 300 битов. Сложность — 275. Со скоростью 230 операций в секунду алгоритм может быть выполнен в 245 секунд или за много лет
Пример 12.33
Мы написали программу, чтобы вычислить разложение 434617. Результат — 709 (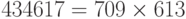 ) Таблица 12.2 показывает значения пар (x и y) и p в этом процессе.
) Таблица 12.2 показывает значения пар (x и y) и p в этом процессе.
Более эффективные методы
В течение прошлых нескольких десятилетий были изобретены несколько методов разложения на множители, они кратко рассматриваются ниже.
| x | y | p |
|---|---|---|
| 2 | 2 | 1 |
| 5 | 26 | 1 |
| 26 | 23713 | 1 |
| 677 | 142292 | 1 |
| 23713 | 157099 | 1 |
| 345589 | 52128 | 1 |
| 142292 | 41831 | 1 |
| 380320 | 68775 | 1 |
| 157099 | 427553 | 1 |
| 369457 | 2634 | 1 |
| 52128 | 63593 | 1 |
| 102901 | 161353 | 1 |
| 41831 | 64890 | 1 |
| 64520 | 21979 | 1 |
| 68775 | 16309 | 709 |
Квадратичное решето
Померанс изобрел метод разложения на множители, называемый методом квадратичного решета. Метод применяет процедуру просеивания, чтобы найти значение x2mod n. Метод используется, чтобы разложить на множители целые числа с более чем 100 цифрами. Его сложность — 0 (ec), где 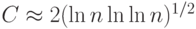 . Обратите внимание, что это – субпотенциальная сложность.
. Обратите внимание, что это – субпотенциальная сложность.
Решето поля чисел
Эндрик Ленстра и Арджин Ленстра изобрели метод разложения на множители и назвали его метод решета поля чисел. Метод использует процедуру просеивания в алгебраической кольцевой структуре к 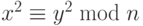 . Показано, что этот метод быстрее для разложения чисел с более чем 120 десятичными цифрами. Его сложность – O(eС) где
. Показано, что этот метод быстрее для разложения чисел с более чем 120 десятичными цифрами. Его сложность – O(eС) где 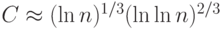 . Обратите внимание, что это — также субпоказательная сложность.
. Обратите внимание, что это — также субпоказательная сложность.
Пример 12.34
Предположим, что есть компьютер, который может выполнить 230 (почти 1 миллиард) битовых операций в секунду. Какое приблизительно время требуется для этого компьютера, чтобы разложить на множители целое число из 100 десятичных цифр, используя один из следующих методов?
a. Метод квадратичного решета
b. Метод решета поля чисел
Решение
Номер с 100 десятичными цифрами имеет почти 300 битов (n = 2300).
ln (2300) = 207 и lnln (2300) = 5.
a. Для метода квадратичного решета мы имеем
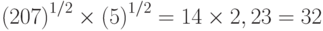 .
.
Это означает, что нам надо e32 битовых операций, которые могут быть сделаны в (e32)/ (230) = 20 часов.
b. При методе решета поля чисел мы имеем 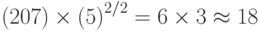 . Это означает, что нам надо e 18 битовых операций, которые могут быть сделаны за
. Это означает, что нам надо e 18 битовых операций, которые могут быть сделаны за 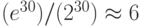 секунд. Однако эти результаты правильны, только если мы имеем компьютер, который может выполнить 1 миллиард битовых операций в секунду.
секунд. Однако эти результаты правильны, только если мы имеем компьютер, который может выполнить 1 миллиард битовых операций в секунду.
Другие проблемы
В лекциях 14-15 мы обсудим прикладные вопросы задачи разложения на множители для вскрытия криптосистем с открытым ключом. Если будут изобретены более эффективные методы разложения на множители, то криптосистемы с открытым ключом вынуждены будут использовать большие целые числа, чтобы противостоять криптоанализу. Изобретатели RSA создали основу для конкуренции методов разложения на множители номеров до 2048 битов (больше чем 600 цифр).