НОУ ИНТУИТ | Теория экономических механизмов. Лекция 9: Аукционы с зависимыми ценностями

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.08.2011 | Доступ: свободный | Студентов: 1543 / 82 | Оценка: 4.50 / 3.50 | Длительность: 18:52:00

ISBN: 978-5-9963-0014-3

Темы: Математика, Экономика

Специальности: Математик, Экономист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Можно еще долго рассуждать о том, что нельзя сделать; в предыдущих лекциях мы об этом много говорили. Но, кажется, пора двигаться дальше и попытаться все же продвинуть наши знания о том, что сделать можно, а также понимание того, что уже делается.

Ключевые слова: ПО, доходность, оптимальная стратегия, обобщение, агент, значение, noisy signal, постановка задачи, информация, model, curses, стоимость, оценка стоимости, нормальное распределение, дисперсия, функция, доказательство, основная модель, анализ, эквивалентность, распределение вероятности, аффилированные величины, определение, супермодулярная функция, случайная величина, равенство, остаток, вектор, отношение правдоподобия, ratio, hazard, rating, интеграл, очередь, симметричность, симметричная функция, плата, выражение, максимум

Введение

Отныне и до конца курса мы будем рассматривать аукционы в том виде, в котором мы это делали в лекциях "3" - "5" . Напомним вкратце классическую постановку задачи дизайна аукционов. Имеется некоторый лот, который выставляется на торги продавцом. В торгах участвуют агентов, каждый из которых хочет приобрести лот за как можно меньшую цену. При этом победа в аукционе приносит агенту пользу v_i — это так называемая внутренняя ценность для агента . 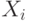В лекциях "3" - "5" внутренняя ценность была функцией исключительно от его собственной полезности x_i , распределенной по некоторому заранее известному распределению X_i , а также от цены, которую ему нужно было заплатить (и уже эта цена зависела от ставок, а значит, и от внутренних ценностей других агентов).

В лекции "5" мы доказали теорему об эквивалентности доходности (теорему 4.1): если скрытые значения агентов x_i распределены одинаково и независимо и все агенты нейтральны к риску, то любое симметричное равновесие любого аукциона дает продавцу один и тот же доход. Иначе говоря, продавцу можно не затруднять себя сложным выбором между, скажем, аукционом второй цены, первой цены и английским аукционом: все равно его доход от формы аукциона не изменится. Конечно, в разделе 4.5 мы немножко оговорились, что могут появиться психологические причины предпочесть один формат другому, да и просто — в аукционе второй цены оптимальная стратегия самоочевидна, а в аукционе первой цены ее нужно вычислять сложным образом, поэтому аукцион второй цены можно применять шире. Но все-таки математически все аукционы были для продавца одинаковы.

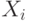Однако в реальной жизни далеко не всегда скрытые значения агентов представляют собой независимые случайные величины. Рассмотрим следующее обобщение: пусть теперь каждый агент не знает точного значения своей ценности, но знает ее примерно. А именно, агент теперь знает значение некоторого случайного неточного сигнала (noisy signal) X_i из диапазона $[0,\omega_i]$ . Ценность лота для агента является некоторой функцией от сигналов всех агентов:

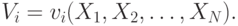
$V_i = v_i(X_1, X_2, \ldots, X_N).$

При этом она также является случайной величиной (так как случайными являются все сигналы 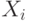X_i ).

Таким образом, теперь цености всех агентов оказываются связанными друг с другом посредством неточных сигналов. Такая постановка задачи называется аукционом с зависимыми ценностями. Существует также модификация аукциона с зависимыми ценностями, в которой кроме неточных сигналов агентов x_i есть еще неточный сигнал , известный только продавцу (у продавца есть уникальная информация об объекте продажи). При этом

$v_i(x_1,\ldots,x_N) = \mathbf E_S\left[\vphantom{1^2}V_i|X_1=x_1,\ldots, X_N=x_N\right].$

В таком случае интересен вопрос о том, имеет ли смысл (для увеличения матожидания своего дохода) продавцу сообщать известный ему неточный сигнал агентам или нет.

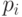Далее мы будем рассматривать первый, более простой случай. Будем по умолчанию полагать, что $v_i(0,0,\ldots,0)=0$ и что $E[V_i] < \infty$ . Кроме того, будем считать, что агенты нейтральны к риску, то есть каждый из них хочет максимизировать матожидание величины V_i-p_i , где p_i - цена, которую придется заплатить за обладание лотом.

Частным случаем аукционов с зависимыми ценностями являются аукционы, в которых существует некоторая общечеловеческая ценность 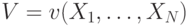$V = v(X_1,\ldots, X_N)$ , а сигналы отдельных агентов 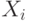X_i распределены вокруг нее (то есть $\mathbf E[X_i|V=v] = v$ ). Типичный жизненный пример такой ситуации — аукционы по разработке месторождений: точный доход от разработки некоторого месторождения примерно одинаковый для всех и никому заранее не известен, но у потенциальных покупателей могут быть примерные его оценки. Поэтому такая модель часто называется "mineral rights model".

К чему приводят зависимые ценности

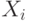Рассмотрим для примера модель с общечеловеческой ценностью (mineral rights model). В описанной выше ситуации возникает так называемое проклятие победителя (winner' curse; вспомните раздел "2.2" ). Так как — это, грубо говоря, среднее значение среди всех X_i , то наибольшее из 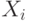X_i неизбежно будет переоценивать !

Возьмем для примера аукцион первой цены. Как только агенту сообщают, что он выиграл аукцион, он понимает, что скорее всего переоценивал значение (так как остальные агенты в таком случае, очевидно, оценивали его меньшим значением). Возможно, что стоимость, которую заплатит агент-победитель, будет даже превышать значение , то есть в итоге он останется в убытке.

Пример 9.1. Рассмотрим простейшую (и самую, наверное, разумную для моделирования реальности) ситуацию, когда оценки агентов распределены нормально и независимо вокруг общечеловеческой ценности . Может показаться, что здесь оценки агентов распределены независимо, и мы возвращаемся в ситуацию аукционов с независимыми ценностями. Но на самом деле это не так: они независимы только при условии известной ценности , а вся соль ситуации как раз в том, что никто эту ценность не знает.

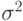Так вот, предположим, что агентов участвуют в аукционе первой цены, и оценка стоимости лота у каждого агента представляет собой нормальное распределение со средним, равным истинной ценности и дисперсией $\sigma^2$ . Тогда функция распределения наивысшей оценки стоимости из агентов будет равна не

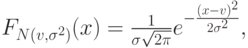
$F_{N(v,\sigma^2)}(x) = \frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x-v)^2}{2\sigma^2}},$

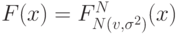а ее -й степени $F(x) = F^N_{N(v,\sigma^2)}(x)$ , что, конечно, гораздо меньше. Вот как растет математическое ожидание максимальной оценки из десяти участвующих агентов для вещи с ценностью и дисперсией :

$\mathbf E\left[\max\limits_{i=1..2}\{X_i\}\right] &=& \int_{-\infty}^{\infty}xNf_{N(1,1)}(x)F_{N(1,1)}(x)dx\approx 1.56419,\\ \mathbf E\left[\max\limits_{i=1..3}\{X_i\}\right] &=& \int_{-\infty}^{\infty}xNf_{N(1,1)}(x)F^2_{N(1,1)}(x)dx\approx 1.84628,\\ \mathbf E\left[\max\limits_{i=1..5}\{X_i\}\right] &=& \int_{-\infty}^{\infty}xNf_{N(1,1)}(x)F^4_{N(1,1)}(x)dx\approx 2.16296,\\ \mathbf E\left[\max\limits_{i=1..10}\{X_i\}\right] &=& \int_{-\infty}^{\infty}xNf_{N(1,1)}(x)F^9_{N(1,1)}(x)dx\approx 2.53875,\\ \mathbf E\left[\max\limits_{i=1..1000}\{X_i\}\right] &=& \int_{-\infty}^{\infty}xNf_{N(1,1)}(x)F^{999}_{N(1,1)}(x)dx\approx 4.24144.\\$

В аукционе с тысячей участников победитель рискует переплатить более чем вчетверо!

Конец примера 9.1.

По этой причине в аукционе первой цены участники должны делать определенную поправку и немного занижать заявляемую стоимость лота. Мы ниже обсудим этот вопрос подробнее и покажем конкретные стратегии для различных типов аукционов.

Стоит также отметить, что "проклятие победителя" зависит от количества участников . Чем больше агентов участвуют в аукционе, тем больше ожидание максимума среди всех оценок стоимости лота, и тем хуже в среднем приходится победителю.

Но это не единственный (и даже не главный) эффект, который появляется в аукционах с зависимыми ценностями. Главным для нас следствием зависимости сигналов является тот факт, что теперь теорема об эквивалентности доходности перестает работать. Причем не просто перестает работать доказательство, а теорема становится по сути неверной. Мы будем обсуждать, как подправить теорему, чтобы суметь хоть что-то сказать в случае зависимых ценностей.

Более того, в 3.2 мы рассказывали о том, каким образом различные модели аукционов оказываются эквивалентными друг другу. Для двух основных моделей аукционов с открытыми ставками — голландского и английского — мы нашли их эквиваленты в терминах закрытых ставок — аукционы первой и второй цены соответственно.

Так вот, в ситуации с зависимыми ценностями аукцион второй цены и английский (восходящий) аукцион перестают быть эквивалентными! Это связано с тем, что в восходящем аукционе у участников, которые остаются активными, по ходу проведения аукциона появляется новая информация — ставки участников, выходящих из аукциона (точнее говоря, значения стоимости лота в те моменты времени, когда эти участники говорили "пас"). Исходя из этих ставок, активные участники могут пытаться оценить скрытые сигналы пасующих агентов. Если в случае аукциона с частными независимыми ценностями они не играли никакой роли, то теперь эти значения могут повлиять на собственные оценки ценности лота оставшихся в игре агентов.

Замечание. С голландским (нисходящим) аукционом все остается эквивалентным: поскольку лот отдают тому агенту, который первым поднял руку, у него по определению не появляется никакой дополнительной информации от ставок других агентов (он ничего не узнает о них).

В дальнейшем мы проведем подробный анализ двух аукционов с закрытыми ставками — первой и второй цены — и английского аукциона с открытыми ставками. Этот анализ позволит нам установить, какой из них лучше с точки зрения продавца и с точки зрения агентов-покупателей. Иными словами, раз уж эквивалентность не выполняется, нужно хотя бы понять, в какую сторону тут все неэквивалентно. Но сначала нам предстоит рассмотреть несколько важных понятий из теории вероятностей, без которых ничего у нас насчет аукционов с зависимыми ценностями доказать не получится.

Дальше >>

Авторизоваться

Теория экономических механизмов

Аукционы с зависимыми ценностями

Введение

К чему приводят зависимые ценности

Вопросы и ответы