Теорема Робертса
Введение
Для функций ценности самого общего вида мы в лекции "Теоремы Эрроу и Гиббарда-Саттертуэйта" уже говорили о теореме Гиббарда-Саттертуэйта (теорема 6.2). Мы доказывали, что если допустить любые порядки на множестве возможных исходов, то реализовать можно только диктаторские функции социального выбора, выгодные ровно одному участнику.
Результат, конечно, весьма печальный. Но неужели ничего нельзя сделать? В математике обычно, если общий факт никак не доказывается или общая конструкция никак не строится, пытаются рассмотреть ограниченную постановку, которая, однако, продолжает иметь смысл.
Для теоремы Гиббарда-Саттертуэйта аналогичный вопрос разумно было бы задать для квазилинейных предпочтений — для ситуации, когда функция полезности каждого агента представляет собой разность между его внутренней ценностью от наступившего исхода и той ценой, которую он должен в результате этого исхода заплатить. Такие предпочтения — более чем естественное предположение; в самом деле, ну как же еще? Но для этих предпочтений теорема Гиббарда-Саттертуэйта уже не слишком-то применима: такого, как там, произвольного порядка предпочтений на всем множестве исходов уже может не получиться построить. Поэтому и теорема о невозможности — а в этой лекции мы опять будем доказывать теорему о невозможности — здесь уже не такая пессимистичная, как теорема Гиббарда-Саттертуэйта. Я бы даже назвал ее не теоремой о невозможности, а теоремой классификации: да, мы классифицируем все реализуемые функции социального выбора, но их окажется вовсе не так мало, и среди них будут практически все естественные функции.
Теорема Робертса, как нетрудно догадаться, доказана была Кевином Робертсом [71]. Его доказательство было достаточно сложным технически, и за деревьями трудно было рассмотреть лес, то есть основную базовую идею доказательства. Поэтому доказательства, которые мы приводим в этой лекции, отличаются от оригинального доказательства Робертса; мы изложим два (достаточно существенно отличающихся друг от друга) упрощенных доказательства теоремы Робертса, представленных не так давно Лави, Му-алем и Нисаном [40].
Здесь, однако, стоит заметить, что мы докажем теорему Робертса только для случая неограниченного множества типов. В реальной жизни множества типов часто бывают ограничены, и структура этих ограничений бывает довольно прихотливой. Но в общем случае ответа на этот вопрос до сих пор нет, есть только частные результаты [26,40]. Поэтому будем излагать то, что есть.
Определения
Для начала напомним основные определения. У механизма есть набор исходов 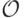 (в этой лекции мы их будем обозначать через
(в этой лекции мы их будем обозначать через 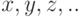 .). Есть
.). Есть  игроков, и у каждого есть свой тип
игроков, и у каждого есть свой тип  . Этот тип — просто набор ценностей, которые игрок может присвоить каждому исходу. Например, в ситуации аукциона по продаже одного предмета, о которой мы часто говорили, набор исходов
. Этот тип — просто набор ценностей, которые игрок может присвоить каждому исходу. Например, в ситуации аукциона по продаже одного предмета, о которой мы часто говорили, набор исходов 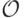 — это то, кому достается вещь (фактически множество исходов равно множеству агентов), а тип
— это то, кому достается вещь (фактически множество исходов равно множеству агентов), а тип  — это функции полезности агента от возможного исхода, которые равны нулю, если эту вещь отдали кому-то другому, или самой ценности, если вещь дали данному игроку:
— это функции полезности агента от возможного исхода, которые равны нулю, если эту вещь отдали кому-то другому, или самой ценности, если вещь дали данному игроку:
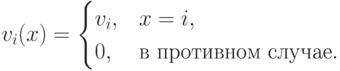
Мы будем называть множество типов неограниченным, если каждый агент теоретически может присвоить каждому исходу любое вещественное число.
Определение 8.1.Множество типов 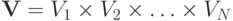 называется неограниченным, если
называется неограниченным, если 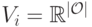 для каждого
для каждого  .
.
В дальнейшем в этой лекции мы всегда будем рассматривать только неограниченные множества типов. Разумеется, суть здесь не в плюс-минус бесконечностях, подошел бы и любой открытый интервал — важно, что очередной агент имеет возможность выбрать ставку, которая строго больше всех остальных (да и вообще может находиться где угодно относительно других ставок — между любыми двумя вещественными числами найдется изрядное количество других вещественных чисел).
Следующий объект, который нас интересует, — это функция социального выбора 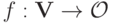 . Можно без потери общности предположить, что
. Можно без потери общности предположить, что  сюръективна; если это не так, мы просто ограничим
сюръективна; если это не так, мы просто ограничим 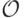 на
на 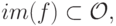 не потеряв ни одного реально возможного исхода, то есть не изменив ни стратегий агентов, ни результатов этих стратегий.
не потеряв ни одного реально возможного исхода, то есть не изменив ни стратегий агентов, ни результатов этих стратегий.
Кроме того, механизм берет с игроков платежи 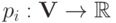 . А игроки квазилинейны, то есть они хотят максимизировать себе функцию дохода (utility function)
. А игроки квазилинейны, то есть они хотят максимизировать себе функцию дохода (utility function)

В этой лекции мы будем вести речь о реализации функций социального выбора в доминантных стратегиях.
Определение 8.2. Функция социального выбора  правдиво реализуема, если существуют функции платежа
правдиво реализуема, если существуют функции платежа 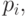 для которых правдивость будет доминантной стратегией.
для которых правдивость будет доминантной стратегией.
От нас в конструкции механизма зависит только 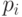 (потому что распределение исходов задается функцией социального выбора), поэтому задача сводится к следующей: нам нужно так подобрать значения
(потому что распределение исходов задается функцией социального выбора), поэтому задача сводится к следующей: нам нужно так подобрать значения 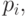 чтобы в конце концов эгоистичные агенты, действуя для максимизации своих
чтобы в конце концов эгоистичные агенты, действуя для максимизации своих 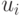 (которые у них квазилинейные), максимизировали
(которые у них квазилинейные), максимизировали  .
.
Формально говоря, для каждого 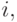 каждого
каждого 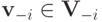 и каждого
и каждого  доходность, которую получит агент, сказав правду, больше доходности, которую получит агент, солгав:
доходность, которую получит агент, сказав правду, больше доходности, которую получит агент, солгав:
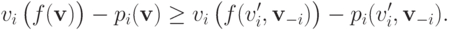
В лекции "Теорема об эквивалентности доходности" мы уже говорили, что все функции социального выбора, оптимизирующие суммарную полезность, она же общественное благосостояние, правдиво реализуемы VCG-платежами (точнее говоря, функция социального выбора, которая оптимизирует общественное благосостояние – она одна, и она реализуема посредством VCG-механизма). Более того, легко видеть, что точно так же реализуемы и функции социального выбора, оптимизирующие взвешенное общественное благосостояние, то есть функции, которые с разными весами учитывают счастье разных агентов.
Задача этой лекции состоит в том, чтобы доказать обратное утверждение. Мы докажем, что оптимизацией таких вот "взвешенно-эффективных" функций социального выбора, собственно, и исчерпываются все возможности, которые у нас есть с квазилинейными агентами.
Теорема 8.1. (Теорема Робертса) Пусть  и множество типов
и множество типов 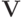 — неограниченное. Тогда для каждой правдиво реализуемой функции социального выбора
— неограниченное. Тогда для каждой правдиво реализуемой функции социального выбора  существуют неотрицательные веса
существуют неотрицательные веса 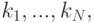 не все равные нулю, и константы
не все равные нулю, и константы 
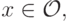 для которых для всех
для которых для всех 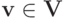

Условия монотонности и их следствия
Оба доказательства теоремы Робертса (да и исходное) основаны на условиях монотонности. Мы сначала докажем, что для правдивой реализуемости  должна удовлетворять этим условиям, а затем, в доказательстве самой теоремы, докажем, что функция, удовлетворяющая таким условиям, имеет требуемый вид. Начнем со свойства слабой монотонности.
должна удовлетворять этим условиям, а затем, в доказательстве самой теоремы, докажем, что функция, удовлетворяющая таким условиям, имеет требуемый вид. Начнем со свойства слабой монотонности.
Определение 8.3. W-MON — слабая монотонность (weak monotonicity, отсюда и W-MON).  удовлетворяет свойству W-MON, если для всех типов
удовлетворяет свойству W-MON, если для всех типов 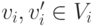 и для любого вектора остальных типов
и для любого вектора остальных типов 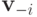 при
при 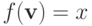 и
и 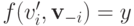

Иначе говоря, если игрок  может изменить свой тип с
может изменить свой тип с  на
на 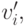 при этом изменив исход с
при этом изменив исход с  на
на 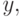 то разность его значений для
то разность его значений для  должна быть не меньше, чем разность его значений для
должна быть не меньше, чем разность его значений для  . Вот так, ненавязчиво, здесь появляются разности, которые будут ключевыми объектами в дальнейших рассуждениях. %Стоит также заметить, что разности нужно использовать из-за квазилинейности.
. Вот так, ненавязчиво, здесь появляются разности, которые будут ключевыми объектами в дальнейших рассуждениях. %Стоит также заметить, что разности нужно использовать из-за квазилинейности.
Лемма 8.1. Всякая доминантно реализуемая функция социального выбора  удовлетворяет W-MON.
удовлетворяет W-MON.
Доказательство. Во-первых, докажем, что 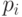 не зависит от
не зависит от  . Другими словами, если функция правдиво реализуется механизмом, то функция платежа уже не зависит от ставки.
. Другими словами, если функция правдиво реализуется механизмом, то функция платежа уже не зависит от ставки.
Предположим противное. Что значит, функция платежа зависит от ставки? Это значит, что есть такие 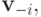
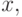
 и
и 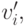 что исход один и тот же, но платеж при этом разный:
что исход один и тот же, но платеж при этом разный:
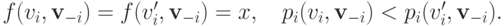
Тогда очевидно, что при векторе типов  игроку
игроку  выгодно солгать. Следовательно, у правдиво реализуемой функции такого быть не может.
выгодно солгать. Следовательно, у правдиво реализуемой функции такого быть не может.
Теперь зафиксируем 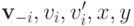 так, как было в определении W-MON. Из-за правдивой реализуемости должно быть верно, что
так, как было в определении W-MON. Из-за правдивой реализуемости должно быть верно, что

иначе при типе  игрок
игрок  сможет улучшить себе доход, солгав
сможет улучшить себе доход, солгав 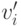 . Аналогично,
. Аналогично,

Сложив эти два неравенства и сократив 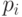 получим искомое условие W-MON. Таким образом, W-MON необходимо для правдивой реализуемости.
получим искомое условие W-MON. Таким образом, W-MON необходимо для правдивой реализуемости.
Второе условие монотонности — свойство PAD (Positive Association of Differences). Это можно перевести как "положительная ассоциация разностей", но большого смысла в этом нет, потому что название не очень "говорящее"; пусть останется просто PAD.
Определение 8.4. Функция социального выбора  удовлетворяет PAD, если для всех
удовлетворяет PAD, если для всех 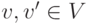 верно следующее: если
верно следующее: если 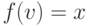 и
и
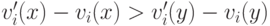
для всех 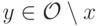 и всех
и всех 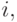 то
то 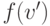 тоже равно
тоже равно  .
.
Свойство PAD тоже рассматривает разности, и оно легко следует из W-MON.
Лемма 8.2. Всякая доминантно реализуемая функция социального выбора  удовлетворяет PAD.
удовлетворяет PAD.
Доказательство. Мы уже доказали, что она удовлетворяет W-MON. Теперь зафиксируем типы  и
и 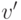 из определения PAD. Схему доказательства, которую мы сейчас применим, мы уже неоднократно отрабатывали на предыдущих лекциях. Введем промежуточные векторы типов, будем менять их пошагово и докажем по индукции, что на каждом шаге тип сохраняется. Промежуточные векторы определим так:
из определения PAD. Схему доказательства, которую мы сейчас применим, мы уже неоднократно отрабатывали на предыдущих лекциях. Введем промежуточные векторы типов, будем менять их пошагово и докажем по индукции, что на каждом шаге тип сохраняется. Промежуточные векторы определим так:
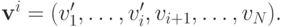
Тогда
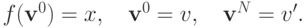
Предположим теперь противное: пусть 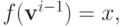 а
а  . Тогда можно применить W-MON:
. Тогда можно применить W-MON:

что противоречит предположению PAD. Значит, 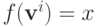 . Утверждение леммы теперь следует индукцией по
. Утверждение леммы теперь следует индукцией по  .
.
Мы будем пользоваться PAD и в еще одной форме. Рассмотрим два вектора 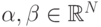 . Будем обозначать
. Будем обозначать  когда имеет место строгое неравенство в каждой компоненте (
когда имеет место строгое неравенство в каждой компоненте ( 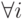
 ). Также обозначим через
). Также обозначим через  нулевой вектор.
нулевой вектор.
Лемма 8.3. Пусть функция социального выбора  удовлетворяет PAD. Зафиксируем
удовлетворяет PAD. Зафиксируем 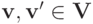 . Если
. Если 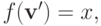 и
и 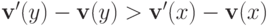 для некоторого исхода
для некоторого исхода  то
то  . \end{lem}
. \end{lem}
Доказательство. Так как в каждой компоненте имеет место строгое неравенство, то, следовательно, можно построить вектор 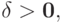 равный разности двух векторов из исходного неравенства:
равный разности двух векторов из исходного неравенства:

Кроме того, для каждого 

Определим теперь новый тип 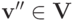 :
:
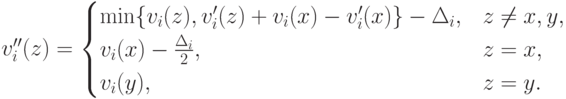
Это сугубо техническая конструкция, которая нужна для того, чтобы придти к противоречию: при такой конструкции из PAD будет одновременно следовать, что 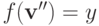 и что
и что  .
.
С одной стороны получаем, что
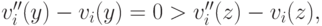
С другой стороны, для 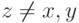
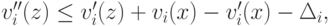
и
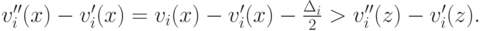
Анналогично для 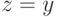 . Тогда из PAD получается, что
. Тогда из PAD получается, что 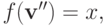 откуда приходим к противоречию.
откуда приходим к противоречию.
Теперь, когда мы изучили все дополнительные леммы об условиях монотонности, можно наконец-то перейти к доказательствам собственно теоремы Робертса.
