Теорема Робертса
Второе доказательство
Второе доказательство использует другое условие монотонности и, естественно, пользуется при этом иным методом анализа. Мы должны также задействовать одно дополнительное условие [52].
Определение 8.5. Задим функцию социального выбора 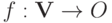 . Будем говорить, что игрок
. Будем говорить, что игрок  принимает решения, если для каждого
принимает решения, если для каждого 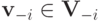 и
и 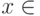 существует такая функция полезности
существует такая функция полезности  что
что 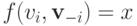 .
.
Проще говоря, игрок  может вынудить выбор любой из альтернатив для любой комбинации типов других игроков (например задавая "достаточно высокое" значение). Мы уже отмечали, что в том случае, когда существуют только две возможные альтернативы, принцип большинства (выбирать альтернативу большинством голосов, где игрок
может вынудить выбор любой из альтернатив для любой комбинации типов других игроков (например задавая "достаточно высокое" значение). Мы уже отмечали, что в том случае, когда существуют только две возможные альтернативы, принцип большинства (выбирать альтернативу большинством голосов, где игрок  "подает голос" за
"подает голос" за  по сравнению с
по сравнению с 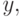 выбирая
выбирая 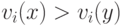 ) реализуем, и при таком подходе нет ни одного игрока, принимающего решения. Однако для трех и более альтернатив, как мы уже знаем из предыдущего доказательства, каждая выполнимая функция социального выбора должна допускать существование как минимум одного принимающего решения игрока. В дальнейшем мы будем пользоваться тем, что такой игрок существует.
) реализуем, и при таком подходе нет ни одного игрока, принимающего решения. Однако для трех и более альтернатив, как мы уже знаем из предыдущего доказательства, каждая выполнимая функция социального выбора должна допускать существование как минимум одного принимающего решения игрока. В дальнейшем мы будем пользоваться тем, что такой игрок существует.
Мы снова доказываем теорему Робертса — теорему 8.1.
Теорема 8.2. Пусть  и
и 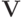 не ограничено. Тогда для каждой правдиво реализуемой функции социального выбора
не ограничено. Тогда для каждой правдиво реализуемой функции социального выбора  существуют такие неотрицательные веса
существуют такие неотрицательные веса 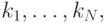 не все равные нулю, и такие константы
не все равные нулю, и такие константы 
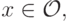 что для всех
что для всех 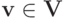

Далее мы без потери общности будем считать, что игрок 1 решающий.
Введем важное обозначение: будем писать
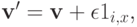
или, что то же самое,
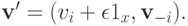
То есть через 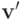 мы будем обозначать вектор, совпадающий с
мы будем обозначать вектор, совпадающий с  за исключением того, что компонента
за исключением того, что компонента 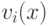 увеличена на
увеличена на 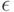 . А через
. А через 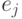 мы будем обозначать единичный вектор вдоль
мы будем обозначать единичный вектор вдоль  -й оси.
-й оси.
Предыдущее доказательство занималось анализом свойств множеств 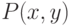 . Здесь мы будем рассматривать не множества, а числа, но числа, тоже достаточно хитро определенные. Следующее определение вводит основной объект нашего анализа [72,73].
. Здесь мы будем рассматривать не множества, а числа, но числа, тоже достаточно хитро определенные. Следующее определение вводит основной объект нашего анализа [72,73].
Определение 8.6. Для каждых двух различных  и для каждого
и для каждого 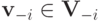 определим
определим
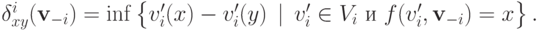
По определению, если 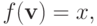 то
то 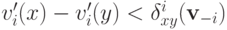 для всех
для всех 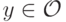 . Иными словами, если зафиксировать
. Иными словами, если зафиксировать 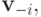 то
то 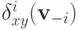 — это минимальное значение разницы между
— это минимальное значение разницы между  и
и  всякий раз, когда
всякий раз, когда  выбирает
выбирает  .
.
Пример 8.1. Для аукциона Викри обозначим через 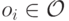 победу игрока
победу игрока  в аукционе. Тогда
в аукционе. Тогда 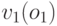 — это ставка, которую ставит агент
— это ставка, которую ставит агент 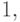 а
а 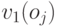 для
для 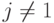 равна нулю (полезность выигрыша любого другого агента для агента
равна нулю (полезность выигрыша любого другого агента для агента  равна нулю). Таким образом, в аукционе Викри
равна нулю). Таким образом, в аукционе Викри  для всякого
для всякого 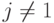 — это ставка, которую должен сделать агент
— это ставка, которую должен сделать агент  для того, чтобы выиграть аукцион.
для того, чтобы выиграть аукцион.
Конец примера 8.1.
Теперь мы хотим исследовать структурные характеристики этого определения для случая неограниченной области и в конце концов показать, что 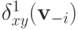 — это аффинная функция от разницы векторов
— это аффинная функция от разницы векторов  . Отсюда и воспоследует свойство аффинной максимизации. Но сначала — немного более техническая лемма, которая установит, что сумма значений
. Отсюда и воспоследует свойство аффинной максимизации. Но сначала — немного более техническая лемма, которая установит, что сумма значений  по циклам небольшой длины равна нулю.
по циклам небольшой длины равна нулю.
Лемма 8.9.
- Для любого
 и любых исходов
и любых исходов 
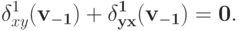
- Для любого
 и любых исходов
и любых исходов 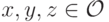
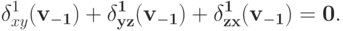
Доказательство. Сначала докажем, что для любого  и любых исходов
и любых исходов  значение
значение 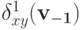 определено (конечно), и
определено (конечно), и
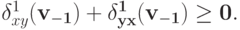
Раз агент  принимает решения, то, значит, существует такая функция полезности
принимает решения, то, значит, существует такая функция полезности 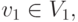 что
что 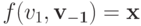 . Тогда
. Тогда
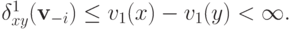
Однако, поскольку агент 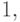 опять же, принимает решения, существует и такая функция полезности
опять же, принимает решения, существует и такая функция полезности 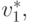 что
что  . Для каждого из тех
. Для каждого из тех 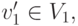 для которых
для которых 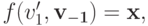 мы по свойству W-MON знаем, что
мы по свойству W-MON знаем, что  . Следовательно,
. Следовательно,
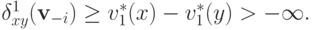
Чтобы доказать, что 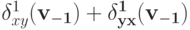 неотрицательно, зафиксируем произвольное
неотрицательно, зафиксируем произвольное  и рассмотрим такую
и рассмотрим такую  что
что
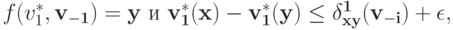
а также такую 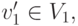 что
что
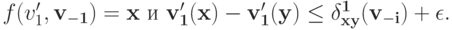
По свойству W-MON мы имеем  . Тогда, значит,
. Тогда, значит,
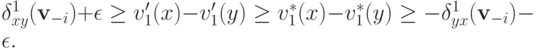
Следовательно, для любого 

откуда и следует искомое неравенство.
Теперь можно доказать собственно утверждения леммы.
- Достаточно показать, что
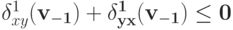 . Для каждых таких
. Для каждых таких 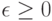 и
и 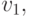 что
что 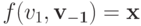 и
и 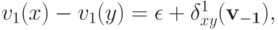 рассмотрим
рассмотрим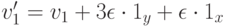 .
.Тогда
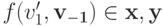 по свойству W-MON. Однако
по свойству W-MON. Однако 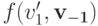 не может быть равно
не может быть равно 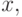 так как
так как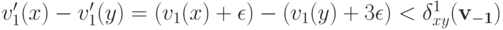 .
.Мы получили, что
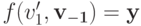 . Но тогда
. Но тогда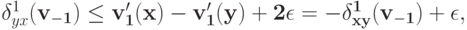
и, таким образом,
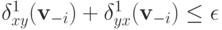 для каждого
для каждого 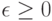 .
. - Зафиксируем
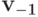 . Рассмотрим такие
. Рассмотрим такие 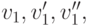 что
что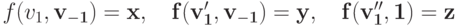
(они существуют, потому что агент
 принимает решения). По правдивости,
принимает решения). По правдивости,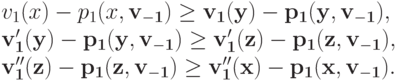
(обратите внимание — опять вдруг откуда ни возьмись появляется парадокс Кондорсе!). Отсюда следует, что
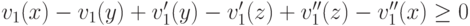 .
.В частности,
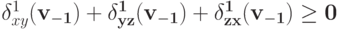 .
.Теперь предположим, что существуют такая функция полезности
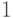 и такие исходы
и такие исходы 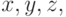 что
что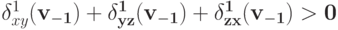 .
.По первому пункту этой леммы,
![[\delta^{1}_{xy}(\bf v_{-1}) + \delta^{1}_{yx}(\bf v_{-1})] + [\delta^{1}_{yz}(\bf v_{-1}) + \delta^{1}_{zy}(\bf v_{-1})] + [\delta^{1}_{zx}(\bf v_{-1}) + \delta^{1}_{xz}(\bf v_{-1})] = 0](/sites/default/files/tex_cache/3b0246b40c434c2b299f0b34f00903cc.png) .
.Таким образом,
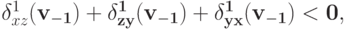
что приводит нас к противоречию.
