Доходы аукционов с зависимыми ценностями
Английский аукцион
Нам удалось доказать, что для аукциона второй цены равновесные стратегии задаются формулой  , где
, где
![v(x,y) = \mathbf E\left[\vphantom{1^2}V_1|X_1 = x, Y_1 = y\right].](/sites/default/files/tex_cache/9e368bbc8f9957f3bf4658c506349707.png)
В этой лекции мы рассмотрим еще две модели аукционов — английский и первой цены — а затем сравним их друг с другом с точки зрения доходов. Наконец, в разделе "10.5" , мы посмотрим насколько эффективными будут аукционы с зависимыми ценностями (окажется, что крайне неэффективными, но мы, опять же, введем дополнительное условие, и жизнь станет проще).
Итак, английский аукцион. В английском аукционе дополнительным источником информации для агента является то, когда другие агенты выходят из игры. В зависимости от этого стратегии активных участников аукциона могут меняться по ходу его проведения.
В такой ситуации уже нет смысла говорить о единой оптимальной стратегии. Симметрическая равновесная стратегия превращается в набор
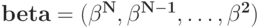
из 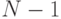 функции. Каждая его компонента
функции. Каждая его компонента 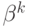 представляет собой функцию
представляет собой функцию  переменных
переменных 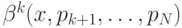 — цену, на которой игрок
— цену, на которой игрок  должен выйти из игры при условии, что его сигнал равен
должен выйти из игры при условии, что его сигнал равен  , в игре остались еще
, в игре остались еще  агентов, а цены остальных вышедших составляли
агентов, а цены остальных вышедших составляли 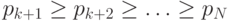 .
.
Опишем следующую стратегию для агентов. Во-первых, вначале, когда все агенты еще активны, положим
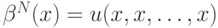
(напомним, что  — это ценность объекта, которая в случае аукционов с зависимыми ценностями оказывается функцией от всех сигналов). Заметим, что
— это ценность объекта, которая в случае аукционов с зависимыми ценностями оказывается функцией от всех сигналов). Заметим, что 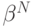 непрерывна и возрастает.
непрерывна и возрастает.
Пусть агент  выходит из аукциона на цене
выходит из аукциона на цене 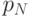 . Тогда положим
. Тогда положим
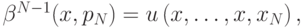
где 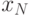 — такое значение сигнала, что
— такое значение сигнала, что  (оно всегда единственно, так как
(оно всегда единственно, так как 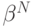 непрерывна и возрастает).
непрерывна и возрастает).
По аналогичному принципу строятся и остальные 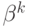 . А именно, если из игры уже вышли агенты с номерами
. А именно, если из игры уже вышли агенты с номерами 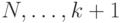 , то
, то
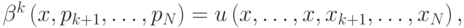
где 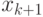 определяется из условия
определяется из условия
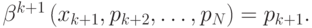
Неформально смысл описанной стратегии очень прост. Всякий раз игрок определяет, стоит ли ему продолжать игру при текущей ставке  . Он спрашивает себя: "Что будет, если я сейчас выиграю аукцион?". Аукцион прямо сейчас выиграть возможно лишь в том случае, когда все остальные агенты прямо сейчас, на ставке
. Он спрашивает себя: "Что будет, если я сейчас выиграю аукцион?". Аукцион прямо сейчас выиграть возможно лишь в том случае, когда все остальные агенты прямо сейчас, на ставке  , решат выйти из игры. Предполагая, что они действуют по аналогичной стратегии, можно определить их скрытые сигналы
, решат выйти из игры. Предполагая, что они действуют по аналогичной стратегии, можно определить их скрытые сигналы  для такого случая из условия
для такого случая из условия
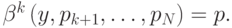
А зная скрытые сигналы всех агентов, можно определить ценность объекта 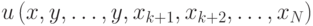 . Очевидно, что продолжать игру стоит тогда и только тогда, когда эта ценность больше, чем
. Очевидно, что продолжать игру стоит тогда и только тогда, когда эта ценность больше, чем  .
.
Теорема 10.1. Описанная выше стратегия  является симметричной равновесной для английского аукциона.
является симметричной равновесной для английского аукциона.
Доказательство. Пусть 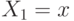 , и все остальные агенты, кроме первого, играют по стратегии
, и все остальные агенты, кроме первого, играют по стратегии  . Рассмотрим значения
. Рассмотрим значения 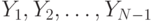 .
.
Пусть 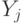 таковы, что агент 1 при следовании стратегии
таковы, что агент 1 при следовании стратегии  выигрывает объект (то есть
выигрывает объект (то есть 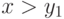 ). В этом случае цена, которую заплатит первый агент, — это цена, на которой из аукциона выходит агент с сигналом
). В этом случае цена, которую заплатит первый агент, — это цена, на которой из аукциона выходит агент с сигналом 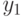 , то есть
, то есть 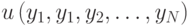 . Так как
. Так как 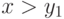 , то выгода игрока
, то выгода игрока  будет положительной:
будет положительной:
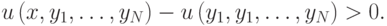
Так как игрок 1 не может повлиять на цену, которую ему придется заплатить, то лучшего результата, чем от использования стратегии  , ему в этом случае все равно не добиться (классическое рассуждение, оно часто помогает в анализе аукционов).
, ему в этом случае все равно не добиться (классическое рассуждение, оно часто помогает в анализе аукционов).
Если же агент  не выигрывает вещь при использовании
не выигрывает вещь при использовании  (то есть если
(то есть если  ), то в случае, если он все-таки решит выиграть аукцион, его доход будет отрицательным:
), то в случае, если он все-таки решит выиграть аукцион, его доход будет отрицательным:
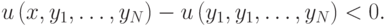
Таким образом, игроку  никогда не выгодно отклоняться от
никогда не выгодно отклоняться от  .
.
Особенность описанного выше равновесия заключается в том, что оно зависит только от оценочной функции  и никак не зависит от распределения сигналов
и никак не зависит от распределения сигналов  . Таким образом, для каждого конкретного
. Таким образом, для каждого конкретного  равновесие
равновесие  не сместится, если изменить распределение сигналов.
не сместится, если изменить распределение сигналов.
Как мы уже обсуждали, в таком случае говорят, что стратегии  образуют равновесие ex post. Такое равновесие лучше, чем равновесия ex ante и interim; в частности, оно обеспечивает свойство отсутствия сожаления (no regret). Проще говоря, даже если после завершения торгов все агенты раскроют точные значения своих сигналов, то никто из них не будет жалеть о своем выборе стратегии: выигравший агент останется с положительной выгодой, а проигравшие поймут, что даже если бы они повысили ставку и выиграли аукцион, они остались бы в убытке.
образуют равновесие ex post. Такое равновесие лучше, чем равновесия ex ante и interim; в частности, оно обеспечивает свойство отсутствия сожаления (no regret). Проще говоря, даже если после завершения торгов все агенты раскроют точные значения своих сигналов, то никто из них не будет жалеть о своем выборе стратегии: выигравший агент останется с положительной выгодой, а проигравшие поймут, что даже если бы они повысили ставку и выиграли аукцион, они остались бы в убытке.
