Доходы аукционов с зависимыми ценностями
Аукцион первой цены
Перейдем теперь к симметричной равновесной стратегии в аукционе первой цены. Сперва, как и ранее, выведем ее эвристически.
Обозначим через  искомую равновесную стратегию, а через
искомую равновесную стратегию, а через 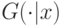 — распределение
— распределение 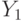 при условии
при условии 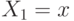 (запомните это обозначение, мы к нему в дальнейшем еще не раз и не два вернемся). Плотность данного распределения будем обозначать, соответственно, как
(запомните это обозначение, мы к нему в дальнейшем еще не раз и не два вернемся). Плотность данного распределения будем обозначать, соответственно, как 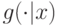 .
.
Тогда ожидаемый доход агента  при его собственном сигнале, равном
при его собственном сигнале, равном  , и ставке
, и ставке 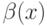 составляет
составляет
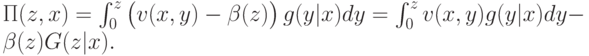
Поскольку  должна быть оптимальной стратегией, получаем следующее дифференциальное уравнение:
должна быть оптимальной стратегией, получаем следующее дифференциальное уравнение:
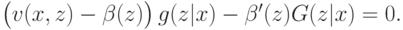
А при симметричном равновесии 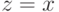 , и в итоге получается
, и в итоге получается
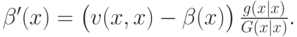
Кроме того, есть и начальное условие:  .
.
Теорема 10.2. В аукционе первой цены симметричное равновесие достигается при использовании следующей стратегии:

где
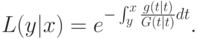
Доказательство. Во-первых, покажем, что 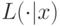 является функцией распределения на интервале
является функцией распределения на интервале ![[0,x]](/sites/default/files/tex_cache/47e2767cb741a37b889f1968c34f8398.png) . По аффилированности, для всех
. По аффилированности, для всех 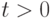
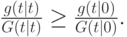
Таким образом,
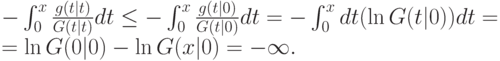
Следовательно, 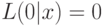 . Кроме того,
. Кроме того,  , и функция
, и функция  является неубывающей.
является неубывающей.
Кроме того, из аффилированности сигналов следует, что

Так как 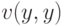 возрастает как функция от
возрастает как функция от  , то
, то  также возрастает как функция от
также возрастает как функция от  .
.
Рассмотрим теперь агента, который делает ставку 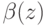 при скрытом сигнале
при скрытом сигнале  . Так как
. Так как  возрастает,
возрастает,
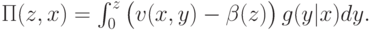
Продифференцировав предыдущее выражение по  , получаем:
, получаем:

Рассмотрим случай  . Так как
. Так как 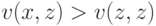 и сигналы аффилированы, то, следовательно:
и сигналы аффилированы, то, следовательно:
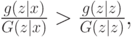
а значит,
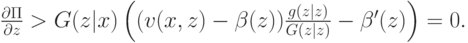
А в случае, когда  , можно совершенно аналогичным способом показать (проведите это рассуждение самостоятельно), что
, можно совершенно аналогичным способом показать (проведите это рассуждение самостоятельно), что 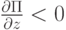 . Из этого следует, что функция
. Из этого следует, что функция 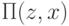 в точке
в точке 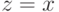 достигает максимума.
достигает максимума.
Полученный результат является обобщением предыдущих результатов. Так, при частных значениях 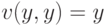 , а при независимых сигналах
, а при независимых сигналах 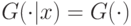 , и, следовательно,
, и, следовательно,
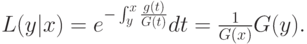
Пример 10.1. Рассмотрим случайные величины 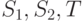 , равномерные и независимые на интервале
, равномерные и независимые на интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Пусть в аукционе участвуют два агента с неточными сигналами
. Пусть в аукционе участвуют два агента с неточными сигналами 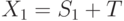 и
и 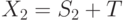 , а общая ценность лота вычисляется следующим образом:
, а общая ценность лота вычисляется следующим образом: 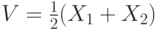 .
.
Наличие  обеспечивает аффилированность сигналов
обеспечивает аффилированность сигналов 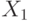 и
и 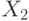 . Так как участника всего два, то
. Так как участника всего два, то 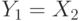 .
.
Совместная плотность 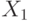 и
и 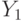 вычисляется отдельно на разных треугольных участках.
вычисляется отдельно на разных треугольных участках.
Путем несложных вычислений можно показать, что для всех  из интервала
из интервала ![[0,2]](/sites/default/files/tex_cache/70fd3f388413505934da60b43afc4088.png)
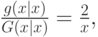
а для всех ![y\in[0,x]](/sites/default/files/tex_cache/f36e05d324f4370233b13e18b730e858.png)
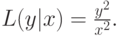
Тогда теорема 10.2 утверждает, что оптимальная равновесная стратегия в данном случае имеет следующий вид:
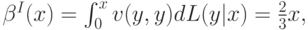
так как  .
.
Конец примера 10.1.
Английский аукцион против аукциона второй цены
В этом и следующем разделах мы будем сравнивать доходность трех описанных типов аукционов в случае, когда агенты действуют в рамках симметричной равновесной стратегии. При наличии аффилированных сигналов и зависимых ценностей уже не действует принцип эквивалентности доходности. Далее будет показано, что английский аукцион превосходит по доходности аукцион второй цены, который, в свою очередь, превосходит аукцион первой цены.
Начнем со сравнения английского аукциона и аукциона второй цены.
Теорема 10.3. Ожидаемый доход от аукциона второй цены не превосходит ожидаемый доход от английского аукциона.
Доказательство. В аукционе второй цены равновесие достигается при использовании стратегии  , где
, где
![v(x,y) = \mathbf E\left[\vphantom{1^2}V_1|X_1=x,Y_1=y\right].](/sites/default/files/tex_cache/1ab8f66443bd39c363087c223a8a0fee.png)
Таким образом, если  , то
, то
![v(y,y) = \mathbf E\left[\vphantom{1^2}u(X_1,Y_1,Y_2,\ldots,Y_{N-1})|X_1=y,Y_1=y\right] = \\ = \mathbf E\left[\vphantom{1^2}u(Y_1,Y_1,Y_2,\ldots,Y_{N-1})|X_1=y,Y_1=y\right] \le \\ \le \mathbf E\left[\vphantom{1^2}u(X_1,Y_1,Y_2,\ldots,Y_{N-1})|X_1=x,Y_1=y\right].](/sites/default/files/tex_cache/ed0dc7787d7f7e303eff2e474a1a802f.png)
Последнее неравенство следует из того, что  возрастает, а сигналы аффилированы.
возрастает, а сигналы аффилированы.
Доход в данном случае вычисляется следующим образом:
![\mathbf E\left[R^{II}\right] = \mathbf E\left[\beta^{II}(Y_1) | X_1 > Y_1\right] = \mathbf E\left[\vphantom{1^2}v(Y_1,Y_1) | X_1 > Y_1\right] \le \\ \le \mathbf E\left[\mathbf E\left[\vphantom{1^2}u(X_1,Y_1,Y_2,\ldots,Y_{N-1})|X_1=x,Y_1=y\right] | X_1 > Y_1\right] = \\ = \mathbf E\left[\vphantom{1^2}u(X_1,Y_1,Y_2,\ldots,Y_{N-1}) | X_1 > Y_1\right] = \\ = \mathbf E\left[\beta^{\mathrm{Eng}2}(Y_1,Y_2,\ldots,Y_{N-1})\right] = \mathbf E\left[R^{\mathrm{Eng}}\right].](/sites/default/files/tex_cache/7c3980470abfdb5eeeabb31834cf1d1f.png)
Здесь через  обозначена стратегия для английского аукциона в случае, когда в игре остаются всего два агента. Цена, на которой предпоследний агент в английском аукционе выходит из игры, — это и есть цена, которую заплатит победитель.
обозначена стратегия для английского аукциона в случае, когда в игре остаются всего два агента. Цена, на которой предпоследний агент в английском аукционе выходит из игры, — это и есть цена, которую заплатит победитель.
Замечание. Английский аукцион дает строго большую доходность, чем аукцион второй цены, только в том случае, когда одновременно присутствуют и зависимость значений, и аффилированность сигналов. Для независимых сигналов или индивидуальных значений эти два аукциона эквивалентны.
