Аукционы с зависимыми ценностями
Симметричная модель
Как и в случае обычных аукционов с независимыми ценностями, далее мы будем рассматривать ситуацию, в которой все агенты находятся в симметричных условиях. В случае, когда у каждого агента была лишь своя, независимая индивидуальная ценность, симметричность означала, что все ценности, как случайные величины, берутся из одного и того же распределения.
В случае зависимых и аффилированных сигналов симметричность понимается двояко. С одной стороны, это симметричность функций ценностей агентов  , а с другой — симметричность распределения случайных сигналов.
, а с другой — симметричность распределения случайных сигналов.
Итак, мы будем полагать, что все 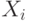 берутся из одного и того же интервала
берутся из одного и того же интервала ![[0,\omega]](/sites/default/files/tex_cache/fc0e1283428eb31676bdded9703922c5.png) , и, кроме того, есть единая для всех агентов функция
, и, кроме того, есть единая для всех агентов функция
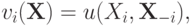
которая является симметричной относительно последних 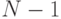 переменных, то есть не изменяющаяся при их перестановке:
переменных, то есть не изменяющаяся при их перестановке:
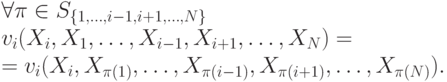
Также будем считать, что плотность совместной вероятности  , определенная на множестве
, определенная на множестве ![[0,\omega]^N](/sites/default/files/tex_cache/453a8ad68f1d996e2bd2540c67055f68.png) , также является симметричной функцией, и что сигналы
, также является симметричной функцией, и что сигналы  аффилированы.
аффилированы.
Определим одну важную функцию:
![v(x,y) = \mathbf E\left[\vphantom{1^2}V_1|X_1 = x, Y_1 = y\right].](/sites/default/files/tex_cache/9e368bbc8f9957f3bf4658c506349707.png)
Она представляет собой математическое ожидание дохода игрока  при условии, что его скрытый сигнал
при условии, что его скрытый сигнал 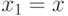 является наивысшим, а наивысший среди всех остальных сигналов равен
является наивысшим, а наивысший среди всех остальных сигналов равен  . Поскольку модель симметрична, функция
. Поскольку модель симметрична, функция  одинакова для всех игроков. Как мы узнали в разделе 9.3, из аффилированности следует, что
одинакова для всех игроков. Как мы узнали в разделе 9.3, из аффилированности следует, что
![\mathbf E\left[\vphantom{1^2}\gamma(Y_1) | X_1 = x^\prime \right] \ge \mathbf E\left[\vphantom{1^2}\gamma(Y_1) | X_1 = x\right].](/sites/default/files/tex_cache/60dce0790e9142684b8c31ec56d21ed2.png)
Следовательно,  неубывает от своих переменных. Кроме того, так как
неубывает от своих переменных. Кроме того, так как  , то
, то  .
.
Равновесие в аукционе второй цены
В заключение этой лекции мы отыщем симметричное равновесие в модели аукциона второй цены. Это самый простой пример анализа аукционов с зависимыми ценностями; более сложные примеры будут в следующей лекции.
Теорема 9.1. В аукционе второй цены симметричное равновесие достигается при выборе следующей стратегии:

Доказательство. Пусть остальные агенты играют по cтратегии 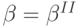 . Вычислим математическое ожидание дохода агента
. Вычислим математическое ожидание дохода агента  с сигналом
с сигналом  при условии, что он поставит
при условии, что он поставит  в качестве своей ставки. Для этого обозначим через
в качестве своей ставки. Для этого обозначим через 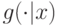 плотность
плотность 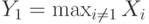 при условии
при условии 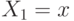 . Чтобы подсчитать ожидание дохода первого агента, нужно проинтегрировать его потенциальный доход
. Чтобы подсчитать ожидание дохода первого агента, нужно проинтегрировать его потенциальный доход 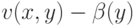 (здесь
(здесь 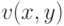 — ценность лота для игрока
— ценность лота для игрока  , а
, а 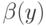 — вторая по величине ставка, то есть плата, которую в аукционе второй цены платит победитель) по всем таким случаям, когда ставка следующего игрока оказывается меньше
— вторая по величине ставка, то есть плата, которую в аукционе второй цены платит победитель) по всем таким случаям, когда ставка следующего игрока оказывается меньше  , то есть когда
, то есть когда 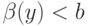 ; поскольку
; поскольку  — неубывающая функция, можно просто интегрировать по
— неубывающая функция, можно просто интегрировать по  от
от  до
до 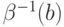 :
:
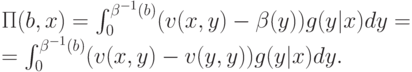
Так как  возрастает по своему первому аргументу, то, следовательно,
возрастает по своему первому аргументу, то, следовательно,
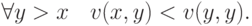
Таким образом, если  заберется за
заберется за  , подынтегральное выражение станет отрицательным, и интеграл начнет уменьшаться. Следовательно, максимум ожидания дохода достигается при использовании
, подынтегральное выражение станет отрицательным, и интеграл начнет уменьшаться. Следовательно, максимум ожидания дохода достигается при использовании 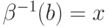 , или, что то же самое, при
, или, что то же самое, при 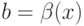 .
.
Пример 9.2. Приведем конкретный пример анализа аукциона второй цены. Пусть в нем участвуют три игрока: 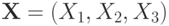 , и все
, и все 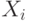 при условии сигнала
при условии сигнала 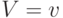 равномерно распределены на отрезке
равномерно распределены на отрезке ![[0,2v]](/sites/default/files/tex_cache/380279c7568bb70ae4d6bf818fe5fb80.png) и независимы. Таким образом,
и независимы. Таким образом,  действительно оказывается средним значением ценностей
действительно оказывается средним значением ценностей 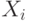 , и они зависят друг от друга исключительно посредством этого общего сигнала. Оставляем читателю удовольствие проверить, что эти случайные переменные действительно будут аффилированы.
, и они зависят друг от друга исключительно посредством этого общего сигнала. Оставляем читателю удовольствие проверить, что эти случайные переменные действительно будут аффилированы.
Для этого примера крайне важной окажется случайная величина, равная максимуму ценностей всех трех агентов. Обозначим ее через
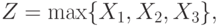
а в каждой конкретной точке, соответственно, 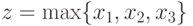 .
.
Плотность распределения 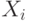 при условии
при условии 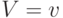 равна
равна 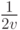 на
на ![[0,2v]](/sites/default/files/tex_cache/380279c7568bb70ae4d6bf818fe5fb80.png) . Следовательно, совместное распределение
. Следовательно, совместное распределение 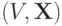 будет равно
будет равно 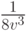 на множестве
на множестве 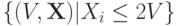 .
.
Заметим, что вся информация, которую мы можем узнать про  , зная значения
, зная значения 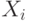 , — это то, что
, — это то, что 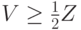 . Значит, совместная плотность
. Значит, совместная плотность  равна
равна
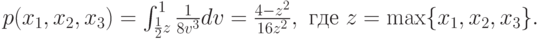
Следовательно, 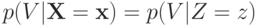 , и на интервале
, и на интервале ![[\frac12z,1]](/sites/default/files/tex_cache/9de368eda74a7bc3192d582db0733953.png) имеем
имеем
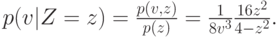
Таким образом,
![\mathbf E\left[\vphantom{1^2}V|\mathbf X=\mathbf x\right] = \mathbf E\left[\vphantom{1^2}V|Z=z\right] = \int_{\frac12z}^1vf(v|\mathbf X=\mathbf x)dv = \frac{2z}{2+z}.](/sites/default/files/tex_cache/79f9ccadd4d2b85c81c973fed617bb59.png)
А это означает, что
![v(x,y) = \mathbf E\left[\vphantom{1^2}V|X_1=x, Y_1 = y\right] = \mathbf E\left[\vphantom{1^2}V|Z = \max\{x,y\}\right] = \frac{2\max\{x,y\}}{2+\max\{x,y\}},](/sites/default/files/tex_cache/a900bcd2aed3c31d79ac23e5703eb425.png)
и, следовательно,
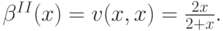
В итоге мы нехитрыми преобразованиями получили явное выражение для оптимальной стратегии поведения агентов в аукционе второй цены с ценностями, которые коррелируют таким вот прихотливым образом. Аналогичный анализ можно провести и в любом другом случае.
