НОУ ИНТУИТ | Теория экономических механизмов. Лекция 3: Принцип выявления предпочтений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.08.2011 | Доступ: свободный | Студентов: 1544 / 82 | Оценка: 4.50 / 3.50 | Длительность: 18:52:00

ISBN: 978-5-9963-0014-3

Темы: Математика, Экономика

Специальности: Математик, Экономист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Принцип выявления предпочтений

Мы уже почти готовы сформулировать и доказать главную теорему этой лекции. В ней пойдет речь об очень интересном факте — оказывается, если какую-то функцию социального выбора можно реализовать при помощи хоть какого-нибудь механизма, ее можно реализовать и при помощи прямого и правдивого механизма!

Важность этой теоремы трудно переоценить — после нее нам во многих случаях можно будет вообще не задумываться о том, что агенты могут лгать. Ведь теперь каждый раз, когда мы раньше предполагали бы, что какой-то механизм реализует функцию социального выбора, мы сможем предполагать, что прямой правдивый механизм тоже реализует эту функцию. И если вдруг окажется, что прямых правдивых реализаций у нее нет, то, значит, у нее и вообще никаких реализаций не имеется; это нам очень поможет, когда мы будем рассматривать теоремы о невозможности.

Исторически принцип выявления (по-английски звучит весьма пышно — revelation principle, но как "принцип откровения" мы решили все-таки не переводить) сначала появился в ограниченной постановке, для доминантных стратегий [22], но вскоре был обобщен на равновесия по Байесу-Нэшу [15,25,54]. Наиболее общая его формулировка, для байесовских игр, была доказана Майерсоном [56,57], и он же продолжил тему принципа выявления еще дальше, на игры, проходящие в несколько раундов (multistage games), когда действия агентов в следующем раунде могут зависеть от исхода предыдущих [58].

Но давайте перейдем к собственно теореме. Мы не будем касаться этих самых многоэтапных игр, а поначалу и вовсе ограничимся формулировкой в доминантных стратегиях. Сформулируем самое "мощное" определение реализации функции социального выбора, скомпоновав свойства правдивой реализуемости и реализумости в доминантных стратегиях.

Определение 3.8. Функция социального выбора 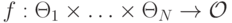$f:\Theta_1\times\ldots\times\Theta_N\to\mathcal O$ правдиво реализуема в доминантных стратегиях^{2Терминов для этого понятия много, в зависимости от контекста по-английски есть несколько разных обозначений: truthfully implementable in dominant strategies, dominant strategy incentive compatible, strategy-proof, straightforward.}, если профиль стратегий

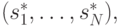
$(s^*_1,\ldots,s^*_N),$

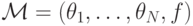где $s^*_i(\theta_i)=\theta_i$ , находится в равновесии доминантных стратегий в игре, индуцированной прямым механизмом $\mathcal M=(\theta_1,\ldots,\theta_N,f)$ , то есть

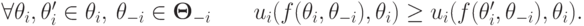
$\forall\theta_i,\theta^\prime_i\in\mathbf\theta_i,\ \mathbf\theta_{-i}\in\mathbf\Theta_{-i}\qquad u_i(f(\theta_i,\mathbf\theta_{-i}),\theta_i)\ge u_i(f(\theta^\prime_i,\mathbf\theta_{-i}),\theta_i).$

Теперь можно и теорему сформулировать.

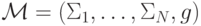Теорема 3.3. (принцип выявления предпочтений в доминантных стратегиях). Пусть для данной социальной функции существует механизм $\mathcal M=(\Sigma_1,\ldots,\Sigma_N,g)$ , который ее реализует в доминантных стратегиях. Тогда правдиво реализуема в доминантных стратегиях.

Доказательство. Несмотря на огромную полезность этого факта, доказательство его будет достаточно простым. Суть происходящего можно объяснить предельно понятной конструкцией построения правдивого механизма по неправдивому.

Предположим, что у нас есть неправдивый механизм 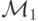$\mathcal M_1$ , в котором агенты находятся в равновесии, но при этом лгут — показывают не свои типы, а другие 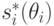$s^*_i(\theta_i)$ . Рассмотрим тогда новый механизм 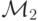$\mathcal M_2$ с немного измененным протоколом — после получения значений от агентов механизм будет их преобразовывать с помощью 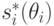$s^*_i(\theta_i)$ , а потом уже подставлять эти значения в функцию получения исхода. Иначе говоря, мы как бы говорим агенту: "Давай мы будем врать за тебя; ты говори правду, а мы уже подставим что надо". Мы это изобразили на рис. 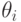3.2; слева изображена исходная схема, в которой агент пользуется стратегией и выдает аукционеру не свой тип $\theta_i$ , а прошедший через стратегию 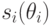$s_i(\theta_i)$ . А справа на том же рисунке стратегию уже "вытащили" из агента и внесли в состав механизма (механизмом справа можно считать все, что внутри штриховой линии). Естественно, в результате агенту будет выгодно говорить такому механизму правду.

Рис. 3.2. Принцип выявления предпочтений

Давайте теперь формально проведем доказательство по этой схеме. 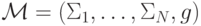$\mathcal M=(\Sigma_1,\ldots,\Sigma_N,g)$ реализует , значит, есть профиль стратегий

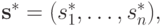
$\mathbf s^*=(s^*_1,\ldots,s^*_n),$

для которого

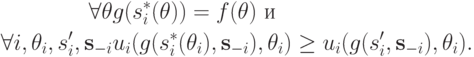
$\begin{align*} \forall \theta & g(s^*_i(\theta))=f(\theta)\text{ и } \\ \forall i,\theta_i,s^\prime_i,\mathbf s_{-i} & u_i(g(s_i^*(\theta_i),\mathbf s_{-i}),\theta_i)\ge u_i(g(s^\prime_i,\mathbf s_{-i}),\theta_i). \end{align*}$

В частности (подставим конкретное 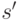$s^\prime$ и $\mathbf s_{-i}$ ),

$\forall i,\theta_i\quad u_i(g(s_i^*(\theta_i),\mathbf s_{-i}),\theta_i)\ge u_i(g(s^*_i(\theta_i),\mathbf s_{-i}^*(\mathbf\theta_{-i})),\theta_i).$

Теперь, поскольку 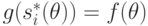$g(s^*_i(\theta))=f(\theta)$ , получим, что

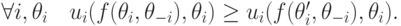
$\forall i,\theta_i\quad u_i(f(\theta_i,\mathbf\theta_{-i}),\theta_i)\ge u_i(f(\theta^\prime_i,\mathbf\theta_{-i}),\theta_i).$

А это и есть в точности определение правдивой реализуемости.

Точно так же можно доказать эту теорему с неправдивыми механизмами, в которых реализуемая функция находится в равновесии по Нэшу или Байесу-Нэшу. Сформулируем общий факт.

Теорема 3.4. (принцип выявления предпочтений) Для любого механизма 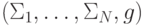$(\Sigma_1,\ldots,\Sigma_N,g)$ и любого равновесия этого механизма 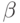$\mathbf\beta$ существует прямой механизм $\mathcal M=(\mathbf Q,\mathbf M)$ , для которого:

стратегии говорить правду находятся в равновесии того же типа, что и $\beta$ ;
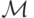результаты работы этого механизма в этом равновесии в точности совпадают с результатами $\mathcal M$ .

Доказательство. Как и в теореме 3.3, нужно просто лгать за агента. Определим компоненты требуемого механизма 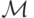$\mathcal M$ как

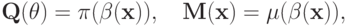
$\mathbf Q(\mathbf\theta) = \pi(\mathbf\beta(\mathbf x)),\quad \mathbf M(\mathbf x) = \mu(\mathbf\beta(\mathbf x)),$

где $\pi$ — индуцированная функция распределения исходного механизма, а $\mu$ — функция выплат исходного механизма. Осталось только проверить, что у этого механизма действительно будет заявленное равновесие; это мы оставим читателю, потому что в теореме 3.3 уже всю структуру доказательства продемонстрировали.

Доказав важную и интересную теорему 3.4, займемся небольшой ее переформулировкой, которая пригодится нам позже. Вспомним, что правдивая реализуемость — это когда

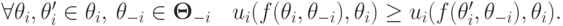
$\forall\theta_i,\theta^\prime_i\in\mathbf\theta_i,\ \mathbf\theta_{-i}\in\mathbf\Theta_{-i}\quad u_i(f(\theta_i,\mathbf\theta_{-i}),\theta_i)\ge u_i(f(\theta^\prime_i,\mathbf\theta_{-i}),\theta_i).$

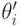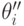А теперь рассмотрим агента и любую пару возможных типов $\theta_i^\prime$ и $\theta^{\prime\prime}_i$ . Если правдивость — доминантная стратегия, то $\forall\mathbf\theta_{-i}\in\mathbf\Theta_{-i}$ выполнено

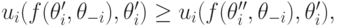
$u_i(f(\theta^\prime_i,\mathbf\theta_{-i}),\theta^\prime_i)\ge u_i(f(\theta^{\prime\prime}_i,\mathbf\theta_{-i}),\theta^\prime_i),$

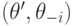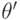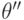потому что при векторе типов $(\theta^\prime,\mathbf\theta_{-i})$ агенту должно быть выгодно сказать $\theta^\prime$ , а не $\theta^{\prime\prime}$ . С другой стороны, для всякого вектора $\mathbf\theta_{-i}\in\mathbf\Theta_{-i}$ выполнено

$u_i(f(\theta^{\prime\prime}_i,\mathbf\theta_{-i}),\theta^{\prime\prime}_i)\ge u_i(f(\theta^\prime_i,\mathbf\theta_{-i}),\theta^{\prime\prime}_i),$

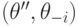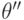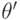потому что при векторе типов $(\theta^{\prime\prime},\mathbf\theta_{-i})$ агенту должно быть выгодно сказать $\theta^{\prime\prime}$ , а не $\theta^\prime$ .

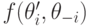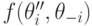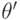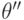Проще говоря, предпочтения агента в той их части, где сравниваются $f(\theta^\prime_i,\mathbf\theta_{-i})$ и $f(\theta^{\prime\prime}_i,\mathbf\theta_{-i})$ , должны измениться, когда его тип меняется с $\theta^\prime$ на $\theta^{\prime\prime}$ или обратно. Это называется свойством слабого обращения преференций (weak preference reversal property).

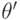Кстати, верно и обратное: если свойство слабого обращения преференций выполняется для всех $\mathbf\theta_{-i}\in\mathbf\Theta_{-i}$ и для всех пар $\theta^\prime,\theta^{\prime\prime}\in\Theta_i$ , то говорить правду — доминантная стратегия для агента . Это легко проверить, если зафиксировать $\theta^\prime$ в определении свойства слабого обращения преференций. А теперь введем новое определение и переформулируем теорему 3.3.

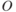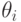Определение 3.9. Множество нижнего контура (lower contour set) возможного исхода при агенте типа $\theta_i$ — это

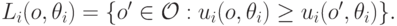
$L_i(o,\theta_i)=\{o^\prime\in\mathcal O:u_i(o,\theta_i)\ge u_i(o^\prime,\theta_i)\}.$

Проще говоря, множество нижнего контура — это те исходы, которые для агента не лучше фиксированного исхода .

Теорема 3.5. (переформулировка принципа выявления доходности) Социальная функция правдиво реализуема в доминантных стратегиях тогда и только тогда, когда для всех , всех $\mathbf\theta_{-i}\in\mathbf\Theta_{-i}$ и всех пар типов $\theta^\prime,\theta^{\prime\prime}\in\Theta_i$ верно

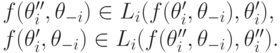
$f(\theta^{\prime\prime}_i, \mathbf\theta_{-i})&\in& L_i(f(\theta^\prime_i,\mathbf\theta_{-i}),\theta^\prime_i), \\ f(\theta^\prime_i, \mathbf\theta_{-i})&\in& L_i(f(\theta^{\prime\prime}_i,\mathbf\theta_{-i}),\theta^{\prime\prime}_i).$

Доказательство. На самом деле мы просто переформулировали факт о том, что механизм реализуем в доминантных стратегиях. Оставляем доказательство этого читателю.

В заключение лекции скажем пару слов о том, что принцип выявления не обеспечивает. Главное упущение, которое может в некоторых случаях осложнять жизнь, заключается в том, что теорема 3.4 конструирует механизм, который имеет то же равновесие, что и исходный механизм, для правдивых стратегий. Но никто не гарантирует, что этот механизм не будет иметь других, неправдивых равновесий. Если они появляются, то вполне возможно, что агенты окажутся в этих неправдивых равновесиях, и анализ существенно осложнится. Но это все, конечно, относится только к равновесиям по Нэшу или Байесу-Нэшу, ведь равновесий в доминантных стратегиях много не бывает (точнее говоря, бывает, но все они эквивалентны).

Дальше >>

Авторизоваться

Теория экономических механизмов

Принцип выявления предпочтений

Принцип выявления предпочтений

Вопросы и ответы