| Невозможно пройти тесты, в окне с вопросами пусто |
Трехмерная графика
Цель лекции: Освоить теоретическую базу, необходимую для понимания функционирования механизмов визуализации трехмерной график в XNA
22.1. Система координат
При работе с трехмерной графикой используется несколько видов систем координат. Для отображения двумерных объектов нам была нужна соответствующая система координат с двумя осями – горизонтальной осью X и вертикальной осью Y. Напомним, что экранная система координат для двумерной графики имеет начало (точку 0,0) в левом верхнем углу монитора, положительная часть оси X располагается справа от начала координат, положительная часть оси Y – снизу.
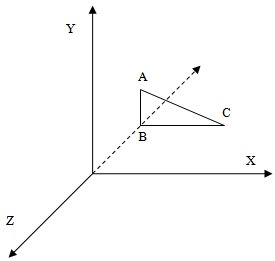
Для работы с трехмерными объектами нам понадобится еще одна ось – она называется ось Z. Существует несколько вариантов трехмерных систем координат, в частности, распространены так называемые правосторонняя и левосторонняя системы. Мы будем пользоваться правосторонней системой – она применяется в XNA Framework. Её схематичное изображение приведено на рис. 22.1.
Особенность этой системы координат заключается в том, что начало координат можно сопоставить с левым нижним углом монитора, положительная часть оси X находится справа от начала координат, положительная часть оси Y – сверху, а положительная часть оси Z – спереди. А это значит, что видимая часть оси Z – это её отрицательная часть. Эта часть оси находится как бы "в глубине монитора", в то время, как положительная часть находится "спереди монитора". На рис. 22.1 пунктиром изображена отрицательная часть оси Z.
В двумерной системе координат существует понятие точки – ее координаты задаются двумя значениями – X и Y. Точки существуют и в трехмерной системе координат – они задаются уже тремя значениями – X, Y, Z.
Точки используют для того, чтобы задавать координаты вершин многоугольников (полигонов), в частности – треугольников. Так, треугольник, изображенный на рис. 22.1, задан тремя точками – A, B, C.
Как правило, более сложные трехмерные объекты строятся именно из треугольников.
В трехмерной графике существует такое понятие, как грань (face). Это – плоский объект, который определяют несколько вершин. В нашем случае обычный треугольник – это именно грань. Из нескольких плоских граней можно собрать объемный объект.
Чем больше треугольников использовано при построении модели – тем более детализированной она получается. Точки, соответствующие вершинам треугольника, который можно изобразить в трехмерном пространстве, называются вершинами. Работая с трехмерной графикой в XNA вам часто придется встречать английский вариант слова вершина – vertex. Возможно, вам встретится множественное число слова вершина: "вершины" выглядит по-английски как "vertices". Иногда для обозначения вершин используют кальку с английского – вертекс.
Треугольник не случайно выбран в качестве базовой геометрической фигуры – во-первых – этот многоугольник всегда является выпуклым, во-вторых – невозможно расположить три точки таким образом, чтобы они не принадлежали одной плоскости. То есть, треугольник – это фигура, которая всегда является выпуклой и плоской, что позволяет с успехом использовать его в целях трехмерной графики.
Несколько граней, из которых состоит трехмерный объект, называются сетью (mesh). Сеть представляет собой набор треугольников.
Еще одно понятие, которое пригодится вам при работе с трехмерной графикой – это понятие вектора. Вектор (vector), так же как и точка, может быть определен тремя параметрами, однако он описывает не положение в пространстве, а направление и скорость движения. Вектор имеет начало и конец, для его полного определения нужно знать координаты точки начала и конца вектора, то есть, вместо трех значений координат нам понадобится уже шесть значений. Однако, если по умолчанию принять за начало вектора начало координат (точку 0,0,0) – тогда для его определения хватит и трех точек.
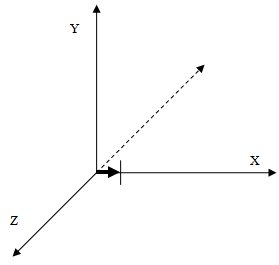
Например, вектор с координатами (1,0,0) означает: "направление – вправо, скорость – 1". Если отложить этот вектор от начала координат, то хорошо видно, что он направлен именно вправо (рис. 22.2).
Направление вектора определяется положением второй точки относительно первой (в нашем случае – положение точки конца вектора, которой задается вектор относительно начала координат), а скорость – длиной вектора – то есть – разницей между начальной и конечной точкой. В нашем случае длина вектора совпадает с координатами его конца.
Существует особый вид векторов – нормали (normals). Нормали могут быть построены для граней и для вершин объекта. Нормали для граней перпендикулярны этим граням. Они используются при расчете цвета объекта.
22.2. Преобразования в трехмерном пространстве
Зная координаты вершин полигонов, из которых состоит объект, мы можем расположить его в пространстве. Теперь нужно разобраться с изменением положения объектов в пространстве. Существует несколько основных операций, которые могут использоваться для перемещения объектов в трехмерном пространстве. Это – перемещение (translation), вращение (rotation) и масштабирование (scale).
Результаты работы графической подсистемы трехмерной игры мы видим на плоском экране монитора – смоделированная компьютером трехмерная сцена проецируется на двумерную поверхность. При проецировании нужно выбрать точку, которая выполняет роль камеры, позволяющей видеть трехмерное пространство. В свою очередь, объекты в трехмерном пространстве могут перемещаться в соответствии с определенными правилами. Для управления всем этим используются несколько матриц. Это – мировая матрица (World Matrix), матрица вида (View Matrix) и матрица проекции (Projection Matrix).
Матрицу можно представить в виде таблицы, состоящей из m строк и n столбцов. В компьютерной графике применяются матрицы 4х4. Первых три столбца этой матрицы отвечают за модификацию координат X, Y, Z вершин объекта, участвующего в трансформации.
Мировая матрица позволяет задавать преобразования – перемещения, вращения и трансформации объектов.
Матрица вида позволяет управлять камерой.
Матрица проекции служит для настройки проекции трехмерной сцены на экран.
Предположим, имеется треугольник, заданный следующими вершинами (табл. 22.1).
При перемещении этого треугольника на 10 позиций по оси X мы должны прибавить по 10 к каждой из координат X его вершин. В результате получится матрица такого вида (табл. 22.2).
Того же эффекта можно достичь, умножив координаты каждой из вершин на мировую матрицу. Для этого координаты вершины представляют в виде матрицы, состоящей из одной строки и четырех столбцов. В первых трех столбцах содержатся координаты X, Y, Z, в четвертом – 1. Мировая матрица представлена в виде таблицы 4х4. Вот как выглядит операция умножения матриц (формула 6.1.):
Умножение матрицы вершины и мировой матрицы
![[\begin{matrix}
20 & 10&5 &1\\
\end{matrix}]
\times
\left[
\begin{matrix}
1 & 0&0 &0\\
0 & 1&0 &0\\
0 & 0&1 &0\\
10 & 0&0 &1\\
\end{matrix}\right]
=
[\begin{matrix}
30 & 10&5 &1\\
\end{matrix}]](/sites/default/files/tex_cache/5bba4a4b35818edbd95a9a1564223a2b.png) |
( 22.1) |
При преобразовании каждая из вершин умножается на мировую матрицу.
Каждое из преобразований в пространстве требует особой настройки мировой матрицы. В формуле 22.2. приведен шаблон мировой матрицы, которая позволяет перемещать объекты в пространстве.
Формула 22.2. Мировая матрица для перемещения объекта
![\left[
\begin{matrix}
1 & 0&0 &0\\
0 & 1&0 &0\\
0 & 0&1 &0\\
\Delta X & \Delta Y&\Delta Z &1\\
\end{matrix}\right]](/sites/default/files/tex_cache/6fa7786a647d561ee1c0f2a2bd7fb824.png) |
( 22.2) |
Здесь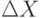 ,
, 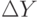 и
и 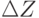 - это приращения координат X, Y и Z.
- это приращения координат X, Y и Z.
Мировая матрица для вращения объектов вокруг оси Х выглядит так (формула 6.3.).
Формула 22.3. Мировая матрица для вращения по оси Х
![\left[
\begin{matrix}
1 & 0&0 &0\\
0 & cos (\alpha)&sin (\alpha) &0\\
0 & -sin (\alpha)&cos (\alpha) &0\\
10 & 0&0 &1\\
\end{matrix}\right]](/sites/default/files/tex_cache/0b6c029c022df07398c1b4871b1fbddf.png) |
( 22.3) |
Здесь  - угол поворота в радианах
- угол поворота в радианах
Мировая матрица для вращения объектов по оси Y выглядит так (формула 6.4.)
Формула 22.4. Мировая матрица для вращения по оси Y
![\left[
\begin{matrix}
cos (\alpha) & 0&-sin (\alpha) &0\\
0 & 1& 0 &0\\
sin (\alpha)& 0&cos (\alpha) &0\\
0 & 0&0 &1\\
\end{matrix}\right]](/sites/default/files/tex_cache/b09d2559c91b95ca4d26ff5c1e5da543.png) |
( 22.4) |
Матрица для вращения объектов вокруг оси Z приведена в формуле 22.5.
Формула 22.5. Мировая матрица для вращения по оси Z
![\left[
\begin{matrix}
cos (\alpha) & sin (\alpha)&0 &0\\
-sin (\alpha) & cos (\alpha)& 0 &0\\
0& 0&1 &0\\
0 & 0&0 &1\\
\end{matrix}\right]](/sites/default/files/tex_cache/ba34a6eb08121725c44836e699b46469.png) |
( 22.5) |
Формула 22.6. представляет матрицу, которая служит для трансформации объектов.
![\left[
\begin{matrix}
\varphi x & 0&0 &0\\
0 & \varphi y&0 &0\\
0 & 0&\varphi z &0\\
10 & 0&0 &1\\
\end{matrix}\right]](/sites/default/files/tex_cache/cfb7d9dacd6022c42600945599e59a3e.png) |
( 22.6) |
Формула 22.5. Мировая матрица для вращения по оси Z
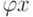 ,
, 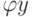 ,
, 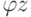 - это коэффициенты масштабирования, которые применяются к вершинам. Они позволяют "сжимать" или "растягивать" объекты.
- это коэффициенты масштабирования, которые применяются к вершинам. Они позволяют "сжимать" или "растягивать" объекты.
Матрица вида влияет на положение камеры – точки, из которой осуществляется просмотр трехмерной сцены.
Матрица проекции позволяет управлять проецированием сцены на экран. В XNA существует два вида проекций.
Первый – это перспективная проекция (Perspective projection). В этой проекции объекты выглядят так же, как мы привыкли их видеть в реальном мире. Объекты, которые расположены дальше, кажутся меньше объектов, расположенных ближе.
Второй вид проекции – это ортогональная проекция. Здесь объекты проецируются на плоскость экрана без учета перспективы.