Определения, структура и развитие систем ИИ

Идею метода проиллюстрируем на примере задачи определения, к какому из двух изначально известных классов А и Б относится искомый объект.

Рассмотрим простейший наглядный пример (рис. 1.43), где представлены исходные точки (распределенные на плоскости по двум признакам - и ) и разбитые на два класса "А" и "Б". Задачей классификации является предсказание принадлежности к тому или иному классу новой (не принадлежащей к известной выборке) точки на плоскости.

Чтобы пример не был абстрактным, скажем, что параметры - это возраст и доход некоторой группы людей, а задача классификации состоит в определении их принадлежности к классу А (потенциальных покупателей определенного товара) и классу Б (тех, кто товар не купит).

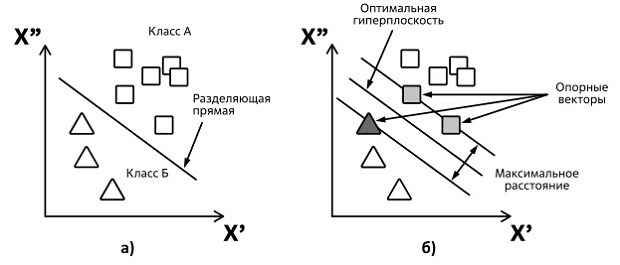
На рисунке построена линия, разделяющая эти два класса (разделяющая прямая). Оптимальной с точки зрения точности классификации является прямая, расстояние от которой до каждого класса максимально. Если известно положение данной прямой, то новые точки (не относящиеся к обучающей выборке) будут классифицироваться по положению относительно данной прямой, определяя их принадлежность классу A или Б.

Мы рассмотрели максимально упрощенный пример с двумя признаками. На практике их может быть произвольное число. В общем случае объект представляется вектором в n-мерном пространстве, где координаты вектора описывают его отдельные атрибуты (например, вес, возраст, доход и т. п). В пространствах произвольной размерности вместо прямых рассматривают гиперплоскости - пространства, размерность которых на единицу меньше размерности исходного. Например, в трехмерном пространстве гиперплоскость - это привычно визуализируемая двумерная плоскость.

По обеим сторонам гиперплоскости ( рис. 1.43 б ) строятся параллельные гиперплоскости. Точки данных, лежащие на одной из двух параллельных гиперплоскостей, которые определяют наибольшее расстояние, называются опорными векторами. Отсюда и происходит название метода. Чем больше расстояние между параллельными гиперплоскостями, тем меньше средняя ошибка классификатора.

Рис. 1.43. Схема, иллюстрирующая идею метода опорных векторов

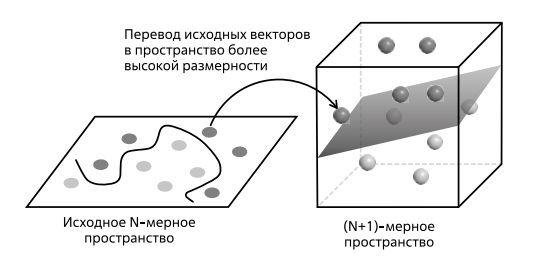
Представим ситуацию, когда множество точек первого и второго класса пересекаются и разделить их прямой линией невозможно (рис. 1.44). При этом при переходе из двумерного пространства параметров в трехмерное (при добавлении еще одного параметра, являющегося комбинацией имеющихся двух) возникает возможность разнести упомянутые классы и провести искомую плоскость. Таким образом, идея метода SVM состоит в переводе исходных векторов в пространство более высокой размерности и построение гиперплоскости, оптимально разделяющей эти классы.

Рис. 1.44. Схема, иллюстрирующая идею метода опорных векторов. Источник: Jeremy Jordan

Для иллюстрации принципа работы алгоритма регрессии^{40Регрессия - односторонняя стохастическая зависимость, устанавливающая соответствие между случайными переменными. В отличие от функциональной зависимости y=f(x), где каждому значению независимой переменной x соответствует одно определенное значение величины y, при регрессионной связи одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y}, упомянутой на рис. 1.42, рассмотрим линейную регрессию на примере функции одной переменной в задаче прогнозирования стоимости жилья. Предположим, что имеются исходные данные о стоимости жилья определенной площади и нам необходимо спрогнозировать цену квартиры некоторой площади, которую мы планируем приобрести. Графически это можно представить как совокупность точек, которые отражают некоторый тренд. Задача линейной регрессии состоит в том, чтобы провести прямую линию так, чтобы она наиболее точно отражала исследуемый тренд. Зная данный тренд, можно предсказать цену для любой площади.

Рис. 1.42. Линейная регрессия, метод наименьших квадратов

Прямая описывается уравнением Y = kx+b, и задача определения этой прямой сводится к нахождению параметров (коэффициентов) линейной зависимости (k и b), которые могут быть найдены путем минимизации суммы квадратов отклонений от каждой точки до нашей прямой (метод наименьших квадратов). Определив коэффициенты, мы можем провести прямую, которая обеспечивает минимальные расстояния от этой прямой до исходных точек. Получив уравнение искомой прямой, найдем значение цены квартиры 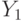при заданном значении площади .

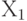Стоит отметить, что определение коэффициентов может быть сделано как аналитически (метод наименьших квадратов), так и с помощью оптимизационных методов. Для задач большой размерности первый способ оказывается алгоритмически более сложным, поэтому применяются методы градиентной оптимизации, такие как метод градиентного спуска.

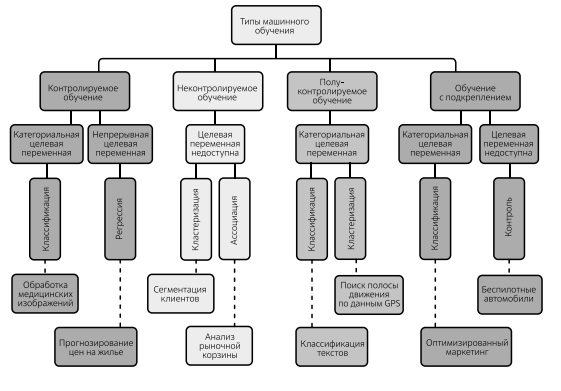
Неконтролируемое обучение (без учителя)

К данному типу обучения относятся алгоритмы, которые обучаются на основе набора данных без каких-либо меток. В качестве примера неконтролируемого обучения можно привести кластерный анализ, где стоит задача разделить объекты на классы по неизвестному признаку. В отличие от классификации, в этом случае нет заранее известных классов. Алгоритм сам должен найти похожие объекты и объединить их в кластеры на основе некоторой заданной функции близости. Типичная задача - сегментация покупателей по предпочтениям или лояльности.

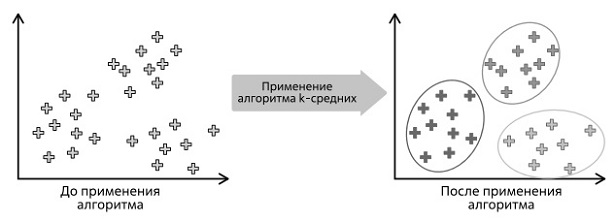
Одним из популярных алгоритмов, применяемых для решения задач кластеризации, является метод k-средних - метод, предложенный в 1950-х годах, суть которого состоит в том, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров ( рис. 1.46).

Весьма наглядное толкование метода приводит автор статьи [56], рассматривая задачу оптимального расположения трех ларьков в поселке. На первом шаге ставим торговые точки случайным образом и смотрим, в какой ларек кому из жителей ближе идти, выделяем три кластера - три группы людей, которым ближе идти до одного из трех ларьков. Перемещаем ларьки в сторону лучшей доступности для посетителей каждой из групп. Повторяем процедуру, то есть опять делим жителей на три кластера и вновь перемещаем ларьки до тех пор, пока не получим решение задачи.

Рис. 1.46. Схема, иллюстрирующая работу алгоритма k-средних

Другой пример, отмеченный на рис. 1.42, - это метод поиска взаимосвязей (ассоциаций) в данных. Поиск подобных взаимосвязей применяется к транзакционным данным в различных отраслях, таких как розничная торговля, банковское дело, страхование. Наиболее распространенный пример - это задача поиска закономерностей в покупаемых вместе товарах. Если вы знаете, какие товары посетители данного магазина покупают вместе, вы можете так расположить продукты в магазине, что продажи вырастут.

Полуконтролируемое обучение

Полуконтролируемое обучение или обучение с частичным участием учителя - это случай, когда обучение происходит на небольшом количестве размеченных и большом количестве неразмеченных данных. Можно сказать, что полуконтролируемое обучение находится между неконтролируемым обучением (без каких-либо размеченных данных) и контролируемым обучением (с полностью размеченными обучающими данными) - см. рис. 1.47.