Основные способы обеспечения безопасности
Пример 7.2. Оценка рисков проекта, основанная на методе экспертной оценки и определения величины потерь с учетом ставки дисконтирования с поправкой на риск.
Годовая норма дисконта rd, принятая для расчета коэффициентов дисконтирования, определена согласно Положению об оценке эффективности инвестиционных проектов при размещении на конкурсной основе централизованных инвестиционных ресурсов бюджета развития РФ, утвержденного Постановлением Правительства РФ от 22.11.97г. №1470 по формуле:
rd = [1 + (rЦБ/100)]/[1 + (i/100)] + P/100 – 1,
где rЦБ - ставка рефинансирования, установленная Центральным банком РФ; i - темп инфляции, объявленный Правительством РФ на текущий год; P - количественно выраженная поправка на риск реализации проекта.
Согласно п. 8 Постановления Правительства РФ от 22.11.97 г. № 1470 поправка на риск (P) может быть определена в зависимости от выполняемых целей проекта в соответствии с рекомендованными в значениями (табл.7.7.). В сложившейся ситуации, когда товар и его производство являются новыми для регионального рынка, предлагаемый уровень риска может быть выбран 19%.
Для более точного обоснования показателя риска проведен дополнительный расчет рисков по методике экспертных оценок. В оценке участвовали три эксперта. Каждому эксперту, работающему отдельно, был предоставлен перечень первичных рисков по всем стадиям проекта, предложено оценить вероятность их наступления, руководствуясь следующей системой оценок:
00 - риск рассматривается как несущественный; 25 - риск скорее всего не реализуется; 50 - о наступлении события ничего определенного сказать нельзя; 75 - риск скорее всего проявится; 100 - риск наверняка реализуется.
| Величина риска | Пример цели проекта | P, % |
|---|---|---|
| Низкий | Вложения при интенсификации производства на базе освоенной техники | 3 - 5 |
| Средний | Увеличение объема продаж соответствующей продукции | 8 - 10 |
| Высокий | Производство и продвижение на рынок нового продукта | 13 - 15 |
| Очень высокий | Вложения в исследования и инновации | 18 - 20 |
Каждому виду риска присвоены соответствующие ему приоритеты и весовые коэффициенты. Первый ранг соответствует весовому коэффициенту 0,1, второй - 0,055.
Показатель риска по каждой ситуации рассчитан исходя из произведения весового коэффициента (Wi) и среднего балла (Vi). Расчетная величина риска определена как сумма показателей риска по каждой стадии. Постадийный расчет первичных рисков приведен в табл.7.8.
| Возможные риски | Эксперты | Средняя Vi | Приоритет | Wi | Pi | ||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||
| Производственный риск | 100 | 100 | 90 | 96,7 | 1 | 0,1 | 9,67 |
| Сбытовой риск | 50 | 50 | 65 | 55 | 2 | 0,055 | 3,02 |
| Финансовый риск | 75 | 75 | 80 | 76,7 | 1 | 0,1 | 7,67 |
| Суммарная вероятность | 20,36 | ||||||
Сопоставив уровень риска, определенный на основании упомянутого Постановления и равный 19%, с полученным результатом экспертов, равным 20,36%, рассчитан средневзвешенный уровень риска проекта в размере 19,68%.
Подставляя принятые значения (rЦБ = 12%, i = 10%, P = 19,68%), получим норму дисконта:
rd = [(1 + 0,12)/(1 + 0,1)] + 0,1968 – 1; rd = 21,50% ? 22%.
Итоговые финансовые показатели проекта будут определяться с учетом полученного значения коэффициента дисконтирования, учитывающего рассмотренные факторы риска.
Рассмотренные примеры показывают относительную простоту использования экспертных оценок для определения общих для проекта финансовых рисков. Однако следует обратить внимание на некоторые слабые стороны, присущие такой оценке общих рисков. Каждое рисковое событие связывается с величиной потерь проекта, которая оценивается как процент от возможной прибыли. На момент действия рискового события величина возможной прибыли обычно не известна. Принятая в данной методике оценка потерь от рискового события в виде процента от прибыли упрощает вычисления, но в некоторых ситуациях может привести к ошибочным рекомендациям. Например, если рисковое событие происходит в период проекта, когда финансовые ресурсы не имеют запасов (финансовый поток проекта близок к нулю), это событие может привести к более ощутимым последствиям по сравнению с таким же рисковым событием, но произошедшим в период с положительным балансом денежных средств. Для более строгой оценки рисковых событий необходим учет абсолютных финансовых показателей факторов риска и баланса предприятия на возможный момент проявления этого рискового события.
Широко распространенными методами количественного анализа рисков проекта являются анализ чувствительности (уязвимости), анализ сценариев и имитационное моделирование рисков по методу Монте-Карло.
Проведение количественного анализа проектных рисков опирается на базисный вариант расчета проекта. В ходе качественного анализа определяются проверяемые на риск факторы (переменные) проекта. Задача количественного анализа состоит в численном измерении влияния изменений рискованных факторов проекта, проверяемых на риск, на поведение критериев эффективности проекта.
В ходе анализа чувствительности (уязвимости) происходит послдовательно-единичное изменение каждой переменной: только одна из переменных меняет свое значение на установленное число процентов и на этой основе пересчитывается новая величина используемого критерия. Простейшим способом, позволяющим проводить грубую оценку риска проекта по методу чувствительности, является анализ точки безубыточности (breakeven point analуsis), широко используемый в международной практике. Под анализом безубыточности понимается исследование взаимосвязи объема производства, себестоимости и прибыли при изменении этих показателей в процессе производства.
При количественной оценке риска проекта применяется анализ сценариев (Scenario analysis). Он представляет собой развитие методики анализа чувствительности проекта в том смысле, что одновременному непротиворечивому (реалистическому) изменению подвергается вся группа переменных проекта, проверяемых на риск. Таким образом определяется воздействие одновременного изменения всех основных переменных проекта, характеризующих его денежные потоки. Важным преимуществом метода является тот факт, что отклонения параметров рассчитываются с учетом их взаимозависимостей (корреляции). В соответствии с расчетами пессимистического варианта возможного изменения переменных, оптимистического и наиболее вероятного варианта определяются новые значения критериев NPV и IRR. Эти показатели сравниваются с базисными значениями и формулируются необходимые рекомендации.
Анализ чувствительности и сценарный анализ - это последовательные шаги в количественном анализе рисков, при этом последний позволяет избавиться от некоторых недостатков метода анализа чувствительности. Однако метод сценариев наиболее эффективно можно применять, когда количество возможных значений NPV конечно. Вместе с тем, как правило, при проведении анализа рисков инвестиционного проекта эксперт сталкивается с неограниченным количеством различных вариантов развития событий. Поэтому на практике используется метод оценки индивидуального риска проекта, помогающий разрешить эту проблему (имитационное моделирование). В основе этого метода лежит вероятностная оценка возникновения различных обстоятельств.
При использовании специализированных пакетов программ для расчета экономической эффективности проектов оценка влияния рисков получается в виде выходных таблиц и графиков, отражающих влияние факторов риска на выходные параметры проекта. График чувствительности проекта к основным параметрам строится с использованием специализированных пакетов "Project expert" и "Альт-Инвест", при этом изменению подвергается один из входных параметров проекта. Последовательно изменяя параметры проекта, разработчик выявляет наиболее критичные из них и вырабатывает меры по уменьшению их влияния.
Цель анализа чувствительности проекта - определение степени влияния варьируемых факторов на финансовый результата проекта. Наиболее распространенный метод, используемый для проведения анализа чувствительности, - имитационное моделирование. В качестве интегральных показателей, характеризующих финансовый результат проекта, используется рассмотренный чистый приведенный доход (NPV). В процессе анализа чувствительности варьируется в определенном диапазоне значение одного из выбранных факторов при фиксированных значениях остальных и определяется зависимость интегральных показателей эффективности от этих изменений.
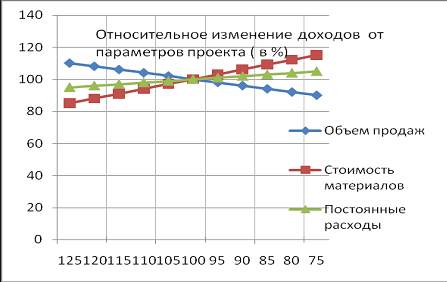
Анализ чувствительности показал, что данный проект допускает снижение цены сбыта на 16%; объем сбыта на 11%; повышение прямых издержек на 14%. На рис 7.7. представлено графическое описание влияния изменения объема продаж, цены реализации, прямых производственных издержек на чистый дисконтированный доход. Точка пересечения графиком оси абсцисс показывает указанные выше параметры.
При проведении анализа чувствительности не измеряется величина риска, а проводится оценка влияния различных факторов на итоги финансовой деятельности предприятия. Анализ позволяет выявить факторы, наиболее влияющие на величину прибыли, и предусмотреть мероприятия, контролирующие эти факторы, найти пути и организовать мероприятия по нейтрализации этих факторов.
Анализ чувствительности (определение критической точки) может быть проведен без применения специальных компьютерных программ исходя из условия безубыточности производства. Рассмотрим вариант такого анализа на примере.
В расчете на заданный период с начала серийного производства общие издержки производства (И) определяются как
И = V*М + F,
где F и V соответственно постоянные и переменные издержки.
Оборот (О) определяется как произведение цены изделия (Ц) на их количество (М):
О = Ц*М.
Условие безубыточности описывает равенство
И = О, или Ц*М = V*М + F.
Таким образом, критический (безубыточный) объем производства равен:
М = F / (Ц – V).
Проанализируем безубыточность условного производственного периода. Выручка предприятия в условном периоде запланирована в размере 14,04 денежных единиц, или можно допустить, что намечено реализовать 14,04 условных штук или 14,04 условных комплектов установок по цене 1 денежная единица. Полные текущие затраты этого периода составляют 12,26 денежных единиц, в том числе постоянные затраты 2,38, переменные затраты - 9,88. Переменные расходы на единицу: V = 9,88 / 14,04 = 0,704. Порог безубыточности получаем из уравнения безубыточности:
1*х = 0,704*х + 2,38, откуда х = 8,04.
Безубыточность достигается при объеме реализации 8,04 денежных единиц.
Критическое значение для постоянных расходов рассчитывается следующим образом: 14,04 = 0,704*14,04 + F, откуда F = 4,16. Постоянные расходы могут возрасти только до этого значения, т.е. могут быть на 42% выше запланированных показателей.
Критическое значение переменных расходов определяется из уравнения оборотов и расходов и рассчитывается по уравнению: 14,04 = = V*14,04 + 2,38, откуда получаем V = 0,84. Таким образом, переменные расходы на единицу продукции могут возрасти до 0,84, т.е. маржа безопасности составляет 46% от первоначально запланированных показателей. Критическое значение цены реализации определяется из условий равенства прибыли нулю. Цена условного изделия (или цена условного комплекта) определена как 1 денежная единица. Определим тот уровень цены, при котором прибыль равняется нулю. Из уравнения оборотов и расходов следует:
14,04*Ц = 0,704*14,04 + 2,38; Ц = 0,87.
Это значит, что отпускная цена при прочих неизменных условиях может быть лишь на 13% ниже запланированной.
В ряде компьютерных программ, например в "Project expert", имеется возможность использовать метод Монте-Карло в инвестиционных расчетах для оценки рисков бизнес-процесса. Суть метода сводится к построению математической модели бизнес-процесса, для которой в зависимости от значений входных данных процесса вычисляются выходные характеристики. Для входных данных задается область изменения и вероятностный закон распределения. В соответствии с правилом метода Монте-Карло производится случайный выбор входных данных в соответствии с принятым для них законом распределения и для построенной модели бизнес-процесса вычисляются его выходные параметры. Процедура повторяется многократно для того, чтобы получить статистику распределения выходных параметров бизнес-процесса. Метод может быть использован для количественного анализа рисков. При этом в качестве выходной характеристики рассматриваются интегральные показатели эффективности бизнес-процесса (чистый приведенный доход, рентабельность инвестиций, внутренняя норма рентабельности и т.д.). Генерирование случайных чисел проводится на компьютере путем получения псевдо-случайных чисел, независимых и случайно распределенных на отрезке [0; 1]. Каждое новое полученное случайное число рассматривается как значение функции распределения для соответствующего значения входных данных. Значение каждой входной переменной определяется как аргумент функции распределения вероятностей этой переменной. Сгенерированные таким образом значения входных переменных подставляются в модель бизнес-процесса и рассчитываются интегральные выходные показатели бизнес-процесса. Описанная процедура повторяется многократно, формируя статистическое распределение выходных параметров эффективности бизнес-процесса. По полученным диаграммам распределения показателей эффективности бизнес-процесса производится оценка его рисков [18].
Для количественного анализа показателей эффективности бизнес-процесса используется ряд абсолютных и относительных показателей:
- математическое ожидание параметра эффективности;
- дисперсия или среднеквадратическое отклонение параметра;
- ожидаемые потери;
- ожидаемый выигрыш;
- коэффициент вариации;
- коэффициент ожидаемых потерь;
- вероятность реализации неэффективного проекта.