Основные способы обеспечения безопасности
Компенсация риска - наиболее сложный и тонкий инструмент обеспечения безопасности предпринимательской деятельности. Возможные пути его реализации основаны на создании системы материальных и/или информационных резервов, составления планов их развертывания. Наиболее эффективным способом борьбы с риском этой группы следует признать метод "поиска гаранта". Как метод обретения или обеспечения надежности этот метод применим и мелкими, и крупными предприятиями.
Так, небольшому предприятию в целях реализации проекта может оказаться полезной более или менее тесная форма интеграции со значительно более мощным партнером. Конкретная форма интеграции может определиться на основе принципа равной взаимной полезности путем структуризации и конкретного анализа хозяйственной ситуации, разработки, оценки и сопоставления вариантов. Универсальным способом в этом смысле оказывается подход, известный под названием "Стратегическое планирование" и являющийся частным случаем "Разработки стратегии предприятия". Стратегия предприятия - это упорядоченная во времени система приоритетных направлений и форм использования его ресурсного потенциала, синтезирующая различные частные стратегии: товарно-рыночную, инвестиционно-финансовую, интеграционную, технологическую, инновационную. Она является единственно надежным основанием для принятия решения о том, какие приемы обеспечения безопасности лучше всего подходят данному предприятию в сфере его инновационной деятельности, т.е. включать в свой состав мероприятия по компенсации риска. Одновременно разработка стратегии позволяет частично снять субъективную неопределенность, поскольку в ходе ее формирования руководящий персонал определяет цели, критерии, мотивы инновационной деятельности на данном предприятии.
Для обеспечения безопасности может оказаться полезным "Метод протоколов риска". Сущность этого метода состоит в следующем. В узловых точках сетевого графика проекта экспертным путем генерируются возможные варианты решений, каждому из которых соотносят некоторые параметры риска (показатели риска). В тех случаях, когда получение количественных оценок показателей риска затруднено или невозможно, используют лингвистические переменные.
Далее на основании полученных оценок по согласованным правилам обсуждается и выбирается решение, вклад которого в уменьшение остаточного риска наибольший. Выбранное решение фиксируется в протоколе вместе с соответствующим обоснованием выбора и необходимыми мерами по компенсации остаточного (или неучтенного) риска.
Снижение общих хозяйственных и финансовых рисков. Приведем наиболее часто встречающиеся факторы риска.
- Риск нереализации профильной технологии предприятия из-за незаключения договора на поставку исходных продуктов.
- Риск недополучения исходных материалов из-за срыва заключенных договоров о поставке.
- Риск невозвращения предоплаты поставщиком.
- Риск незаключения договоров на реализацию производственной продукции (риск нереализации произведенной продукции).
- Риск неполучения или несвоевременного получения оплаты за реализованную без предоплаты продукцию.
- Риск отказа покупателя от полученной и оплаченной им продукции (возврат).
- Риск срыва собственных производственных планов или инновационных проектов.
- Риск неверного прогнозирования ситуации и получения неправильных исходных данных.
- Риск неполучения внешних инвестиций и кредитов.
Основные инструменты защиты от рисков на промышленных предприятиях представлены в табл.7.2 [16]
| Инструмент | Мероприятия |
|---|---|
| Распределение | Методы и регламент распределения риска по этапам проекта |
| Методы и регламент распределения риска между субъектами предпринимательства | |
| Факторинг | |
| Аутсорсинг | |
| Учет векселей | |
| Локализация | Программы и приказы по выделению венчурных подразделений |
| Программы и приказы по выделению венчурных предприятий в структуре холдинга | |
| Диверсификация | Программа расширения деятельности |
| Регламент определения пропорций между видами деятельности | |
| Программы расширения номенклатуры поставщиков и покупателей | |
| Методы и регламент пропорций между объемами поставок по различным каналам | |
| Методы и регламент пропорций между объемами продаж различным покупателям | |
| Регламент распределения капитала между различными проектами | |
| Регламент использования различных валют при внешнеэкономической деятельности | |
| Локализация | Программа выделения венчурных подразделений |
| Программа выделения венчурных предприятий в составе холдинга | |
| Уклонение | Методы принятия решений об отказе от действий, связанных с высокими рисками |
| Компенсация | Программа долгосрочных целей и программа их достижения |
| Модели развития хозяйственной среды, партнеров и конкурентов | |
| Прогноз емкости рынка поставок и продаж | |
| Рекламные кампании и PR-акции | |
| Стратегии конкурентной борьбы | |
| Методы предупреждения рисков и программы обучения | |
| Персонала этим методам | |
| Внешнее страхование | Контракты страхования производственного вреда сотрудников |
| Контракты страхования имущества предпринимательской структуры | |
| Контракты страхования ответственности предпринимательской структуры | |
| Контракты страхования риска неплатежей | |
| Лимитирование | Ограничение объема продаж одному покупателю |
| Ограничение объема поставок по одному каналу | |
| Ограничение объема кредитных ресурсов одному заемщику | |
| Ограничение позиций одного эмитента в портфеле финансовых инвестиций | |
| Хеджирование | Опционы |
| Форвардные контракты | |
| Фьючерсные контракты | |
| Своп-операции | |
| Самострахование | Регламент формирования резервного фонда |
| Регламент формирования специальных резервноых фондов | |
| Регламент формирования сстраховых запасов оборотных активов |
При использовании программы "E-Project" вероятность рисков и величина риска на каждый момент проекта вычисляется и может быть представлена в виде графиков или цифровых значений.
Для определения величины коммерческих рисков вычисляются все случайные величины, принимающие участие в реализации проекта. Примером таких случайных величин могут служить планируемые объемы реализации продукции, планируемые цены на закупаемые товары и комплектующие изделия, планируемые расходы на коммунальные услуги и т.д. Оценить характеристику одного случайного параметра обычно удается довольно легко. В качестве характеристик случайных величин используются его математическое ожидание и дисперсия. Для вычисления этих параметров используются максимальное и минимальное значения случайной переменной. Предполагая, что внутри определенного диапазона изменения случайной величины ее вероятность распределяется по закону, близкому к нормальному, можно определить среднеквадратическое отклонение ? как одну шестую часть разницы между максимальным и минимальным значением параметра. Среднее значение переменной задается во входных данных проекта. К случайным величинам отнесены все данные, характеризующие себестоимость товара или услуги, цену реализации, все компоненты постоянных и переменных затрат. Для всех этих характеристик проекта вводятся три значения: наиболее вероятное (которое принимается за математическое ожидание), максимальное и минимальное. По введенным максимальному и минимальному значениям определяется дисперсия случайной величины.
Использование дисперсии в практических расчетах и ее интерпретация требуют известных навыков. Удобнее всего использовать сравнение дисперсий при обработке данных о конкретных одноименных показателях за различные периоды или по разным сферам и сегментам рынка. Среднеквадратическое отклонение ? исчисляется в отличие от дисперсии в той же размерности, что и сама случайная величина. Может, именно это послужило причиной его широкого применения для характеристики отклонений и вероятностной оценки поведения случайной величины. В частности, среднеквадратическое отклонение имеет чрезвычайно важное значение для критериальной характеристики так называемого принципа практической уверенности.
Среднеквадратическое отклонение позволяет определить количественные интервалы принципа практической уверенности в виде правила трех сигм ?: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения. Таким образом, зная среднеквадратическое отклонение, можно с достаточной уверенностью сказать, что все рассеивание данной случайной величины укладывается в интервал М(х) ± 3?(х).
Вероятность того, что значение случайной величины будет находиться в этом интервале при нормальном распределении и частоте, равна 0,9973. Вероятность того, что абсолютная величина отклонения превысит утроенное среднеквадратическое отклонение, очень мала (0,0027). Это может произойти лишь в 0,27% случаев. Такая надежность в экономических, в частности в ценностных расчетах, в рыночных условиях в основном бывает не нужна, поскольку руководство предприятия в ходе контроля за финансово-хозяйственной деятельностью может корректировать принимаемые решения. Поэтому в предпринимательской деятельности надежнее пользоваться принципом разумной уверенности, или принципом разумного риска.
Принцип разумной уверенности, или разумного риска, предпринимательской деятельности означает, что в принятии решения руководствуются таким соотношением вероятностей осуществления и неосуществления события, при котором примерно 2/3 шансов благоприятствует успеху и 1/3 шансов ему не благоприятствует. Неблагоприятная треть шансов является стимулятором для рассмотрения и принятия мер по их предотвращению. Этому правилу при нормальном распределении соответствует интервал значений случайной величины, равный отклонению от математического ожидания в пределах среднеквадратического отклонения, т.е. М(х) ± ?(X).
Экономисту часто бывает привычнее пользоваться для характеристики отклонений процентными соотношениями. Коэффициент вариации при нормальном распределении вероятностей характеризует интервал отклонения случайной величины при вероятностном исходе, соответствующем 2/3 шансов "за" и 1/3 шансов "против" в процентном отношении к математическому ожиданию. Поэтому можно считать, что коэффициентом вариации в ценностных расчетах целесообразно и необходимо пользоваться, он дает вероятностную базу для экономических расчетов.
Значения выходных характеристик производственного процесса определяются как результаты вычислений с характеристиками случайных процессов. Наиболее распространенный вид вычислений - сумма и произведение случайных величин.
При определении значений сумм и произведений случайных величин используются следующие зависимости для выполнения преобразований.
Для суммы случайных величин x, y математическое ожидание М и дисперсия D имеют вид:
M(x + y) = M(x) + M(y),
D(x1 + x2 +…+ xn) = D(x1) + D(x2) +…+ D(xn).
Для произведения случайных величин, если М = xy:
M(xy) = M(x)*M(y),
D(M) = dM/dx * D(y) + dM/dy * D(x),
где dM/dx и dM/dy соответственно производные переменной M по аргументам x и y.
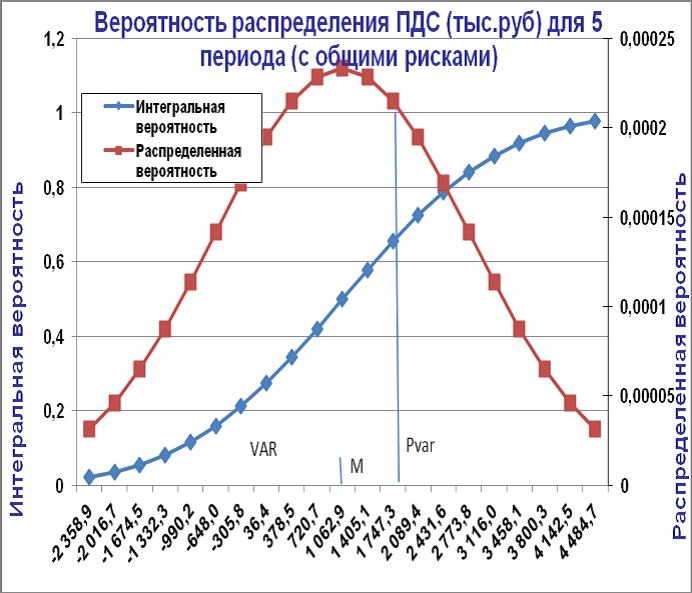
Поскольку выходные параметры производственных процессов представляют собой композицию многих случайных переменных, с большой долей достоверности можно предположить, что выходные параметры таких процессов будут подчиняться нормальному закону распределения. Например, в качестве выходной формы программы "E-Project" предлагается вероятность распределения доходов на каждый отчетный период. Пример такого графика представлен на рис.7.1.
На диаграмме представлены распределенная вероятность, показывающая абсолютное значение вероятности достижения указанного уровня дохода, и интегральная вероятность, показывающая интегральное значение вероятности появления дохода от самого минимального ( в данном примере –2358 тыс. руб.) до любого возможного значения в пределах диапазона изменения дохода. Интегральная вероятность позволяет оценивать вероятность получения доходов в любом заданном интервале доходов. Например, на представленном рисунке величина дохода между значениями 0 и 800 тыс. руб. будет определяться как разница соответствующих значений интегральной вероятности 0,4 – 0,2 = 0,2, что соответствует 20%.