Тексты. Кодирование
В основе каждого текста лежит алфавит – конечное множество символов. В основе текстов на русском языке лежит алфавит, называемый кириллицей, состоящий из 33 строчных и 33 заглавных букв алфавита. Тексты английского языка построены на основе латиницы – алфавита, содержащего 26 строчных и 26 заглавных букв. Конечно алфавит, на основе которого строятся тексты на естественных языках, содержит не только буквы, но и цифры, знаки операций и множество других специальных символов.
Пусть задан алфавит  , содержащий m символов:
, содержащий m символов:
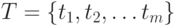
Словом  в алфавите
в алфавите  называют любую последовательность символов алфавита:
называют любую последовательность символов алфавита:
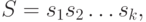
где 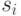 – это символы алфавита. Число символов в слове –
– это символы алфавита. Число символов в слове –  называют длиной слова.
называют длиной слова.
Справедливо утверждение:
Число различных слов длины k, которые можно построить в алфавите из m символов, равно: 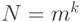
Справедливость утверждения легко доказывается по индукции.
Базис индукции: при 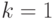 , утверждение справедливо, поскольку словами длины 1 являются m символов алфавита.
, утверждение справедливо, поскольку словами длины 1 являются m символов алфавита.
Шаг индукции: Пусть утверждение справедливо при некотором  . Это означает, что построено
. Это означает, что построено 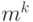 слов длины
слов длины  . Из каждого слова можно построить m новых слов длины
. Из каждого слова можно построить m новых слов длины  , приписывая к слову поочерёдно m символов алфавита. Таким образом, слов длины
, приписывая к слову поочерёдно m символов алфавита. Таким образом, слов длины  будет:
будет:
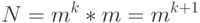
Это простое, но важное утверждение, которое в том или ином виде используется при решении различных задач.
Алфавит компьютера
Тексты, которые хранятся в памяти компьютера, используют один из самых примитивных алфавитов, состоящий всего из двух символов:
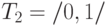
С другой стороны мы знаем, что в памяти компьютера можно хранить не только тексты на различных естественных языках, но и графику, музыку и другую информацию различного вида. Как такое возможно? Разберемся с текстами. Пусть есть два алфавита –  , состоящий из
, состоящий из  символов и алфавит
символов и алфавит 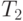 . Представление текстов в алфавите
. Представление текстов в алфавите  текстами в алфавите
текстами в алфавите 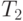 называется кодированием. Простейший способ кодирования состоит в том, чтобы символы алфавита
называется кодированием. Простейший способ кодирования состоит в том, чтобы символы алфавита  кодировать словами конечной длины алфавита
кодировать словами конечной длины алфавита 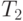 . Умея кодировать каждый символ, можно кодировать любой текст символ за символом.
. Умея кодировать каждый символ, можно кодировать любой текст символ за символом.
Какова должна быть минимальная длина слов в алфавите 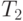 , чтобы было возможно этими словами закодировать алфавит из
, чтобы было возможно этими словами закодировать алфавит из  символов? Очевидно, что длина может быть определена из условия:
символов? Очевидно, что длина может быть определена из условия:

Если, например,  , то наименьшее возможное значение
, то наименьшее возможное значение  равно 5.
равно 5.
Долгое время при работе с текстами, сохраняемыми в компьютере, использовался код ASCII, в котором каждый символ алфавита кодировался словом из 8 бит (одним байтом). Такой алфавит, содержащий 256 различных символов, мог включать латиницу и кириллицу, цифры, знаки операций, знаки препинания, скобки и другие символы. Но все-таки этого алфавита явно недостаточно, чтобы можно было хранить в памяти компьютера тексты на любых естественных языках. Чтобы такое было возможно, необходимо, чтобы алфавит включал алфавиты всех известных естественных языков, в том числе алфавит украинского языка, готику, греческий алфавит, алфавит языка иврит, арабского языка, китайские и японские иероглифы.
В сегодняшних компьютерах для хранения текстов используется кодировка из двух байтов, называемая UNICODE кодировкой, позволяющая словами из 16 битов кодировать алфавит, содержащий  символов. Для большинства существующих естественных языков такого алфавита хватает для представления текстов, записанных на этих языках.
символов. Для большинства существующих естественных языков такого алфавита хватает для представления текстов, записанных на этих языках.
Задача 9:
Автомобильный номер состоит из 7 символов. В качестве символов используются 30 букв и 10 цифр. Символ кодируется минимально возможным набором битов. Номер представляется целым числом байтов. Какую память требуется иметь для хранения 1000 номеров.
Ответ: Примерно 6 Кб.
Решение: Алфавит для записи текстов, представляющих номера автомобилей, содержит 40 символов (30 букв и 10 цифр). Для кодировки такого алфавита потребуются двоичные слова длины 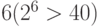 . Для кодировки всего номера потребуется
. Для кодировки всего номера потребуется  бита. Округляя в большую сторону до целого числа байтов, получим, что для хранения одного номера потребуется 6 байтов. Для хранения 1000 номеров достаточно 6 Кб.
бита. Округляя в большую сторону до целого числа байтов, получим, что для хранения одного номера потребуется 6 байтов. Для хранения 1000 номеров достаточно 6 Кб.
Задача 10:
В командной олимпиаде по информатике участвуют ученики из школ, номера которых заданы двузначными числами. В команде может быть не более 7 учеников. Какой минимальный объем памяти потребуется для хранения 500 номеров участников олимпиады, если каждый номер представляется целым числом байтов?
Ответ: Достаточно 1 Кб.
Решение: Номер участника может состоять из номера школы и номера участника в данной школе. Для 100 номеров школ достаточно 7-и битов (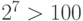 ). Для номера участника в школе достаточно 3-х битов (
). Для номера участника в школе достаточно 3-х битов ( ). Поэтому для хранения номера участника достаточно 10 битов. Округляя в большую сторону до целого числа байтов, получим, что 2-х байтов достаточно для хранения номера. Для хранения 500 номеров достаточно одного килобайта.
). Поэтому для хранения номера участника достаточно 10 битов. Округляя в большую сторону до целого числа байтов, получим, что 2-х байтов достаточно для хранения номера. Для хранения 500 номеров достаточно одного килобайта.
Задача 11:
Алфавит состоит из 4-х букв {М, У, Х, А} Слова длины 5 перечисляются в лексикографическом порядке. Нумерация слов начинается с единицы. Какое слово в этом перечислении стоит под номером 1016, под номером 365?
Ответ: ХХХМХ; ММУХА
Решение: Число различных слов длины 5 в 4-х буквенном алфавите равно 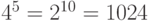 . При перечислении их в алфавитном (лексикографическом) порядке под номером 1 стоит слово ААААА, под номером 1024 – слово ХХХХХ. В задачах экзамена ЕГЭ обычно требуется указать слово, стоящее близко к концу перечисления, что имеет место в нашей задаче, в которой требуется назвать слово под номером 1016, стоящее в первом десятке с конца перечисления. Поэтому для решения задачи достаточно выписать десять слов в обратном лексикографическом порядке, что и дает слово ХХХМХ.
. При перечислении их в алфавитном (лексикографическом) порядке под номером 1 стоит слово ААААА, под номером 1024 – слово ХХХХХ. В задачах экзамена ЕГЭ обычно требуется указать слово, стоящее близко к концу перечисления, что имеет место в нашей задаче, в которой требуется назвать слово под номером 1016, стоящее в первом десятке с конца перечисления. Поэтому для решения задачи достаточно выписать десять слов в обратном лексикографическом порядке, что и дает слово ХХХМХ.
Для ответа на второй вопрос, где требуется найти слово, стоящее в середине перечисления, такой явный способ выписывания слов не подходит. В этом случае следует применять более общий подход, применимый для всех случаев. Для его понимания нужно вспомнить системы счисления.
Поставим в соответствие буквам алфавита цифры (А – 0, М – 1, У – 2, Х -3). При задании этого соответствия учитывается принятый порядок следования букв в алфавите. Число букв задает число используемых цифр, а тем самым задает основание системы счисления. Введенное соответствие букв и цифр порождает соответствие между словами в алфавите и числами в соответствующей системе счисления, в нашем случае – четверичной системе счисления. При лексикографическом перечислении слов длины  слову, стоящему под номером N, соответствует число
слову, стоящему под номером N, соответствует число 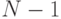 в четверичной системе счисления, содержащее k цифр, включая незначащие нули. Так, слову под номером 1, состоящему из 5 букв, соответствует число 0, записанное как 00000, или, после замены цифр буквами, - ААААА. Поэтому для решения задачи, зная N, достаточно получить запись числа N-1 в четверичной системе, а затем заменить цифры буквами.
в четверичной системе счисления, содержащее k цифр, включая незначащие нули. Так, слову под номером 1, состоящему из 5 букв, соответствует число 0, записанное как 00000, или, после замены цифр буквами, - ААААА. Поэтому для решения задачи, зная N, достаточно получить запись числа N-1 в четверичной системе, а затем заменить цифры буквами.
Получим решение задачи этим способом для N = 1016 и N = 365.
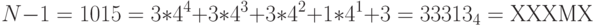

Задача 12:
Алфавит состоит из 3-х букв {А,М, П} Слова длины 4 перечисляются в лексикографическом порядке. Нумерация слов начинается с единицы. Под каким номером стоит слово МАМА, слово - ПАПА?
Ответ: 31; 61
Решение: В троичной системе слову МАМА соответствует число 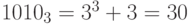 . В перечислении, где нумерация начинается с 1, номер этого слова равен 31.
. В перечислении, где нумерация начинается с 1, номер этого слова равен 31.
Слову ПАПА соответствует число  .
.
