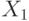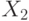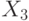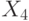Тверской государственный университет
Опубликован: 06.10.2013 | Доступ: свободный | Студентов: 1393 / 338 | Длительность: 02:37:00
Тема: Образование
Специальности: Преподаватель
Лекция 3:
Логика. Логические функции. Решение уравнений
Аннотация: Представление логических функций. Программа на языке C# для решения логических уравнений.
Ключевые слова: законы логики
Большое количество задач ЕГЭ посвящено логике высказываний. Для решения большинства из них достаточно знания основных законов логики высказываний, знания таблиц истинности логических функций одной и двух переменных. Приведу основные законы логики высказываний.
- Коммутативность дизъюнкции и конъюнкции:
- Дистрибутивный закон относительно дизъюнкции и конъюнкции:
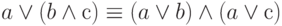
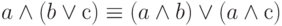
- Отрицание отрицания:
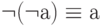
- Непротиворечивость:
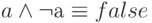
- Исключающее третье:
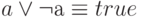
- Законы де-Моргана:
- Упрощение:
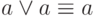
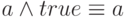
- Поглощение:
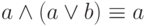
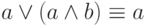
- Замена импликации
- Замена тождества
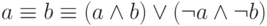
Представление логических функций
Любую логическую функцию от n переменных –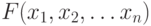 
можно задать таблицей истинности. Такая таблица содержит 
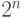наборов переменных, для каждого из которых задается значение функции на этом наборе. Такой способ хорош, когда число переменных относительно невелико. Уже при 
представление становится плохо обозримым.
Другой способ состоит в том, чтобы задавать функцию некоторой формулой, используя известные достаточно простые функции. Система функций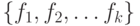 
называется полной, если любую логическую функцию можно выразить формулой, содержащей только функции 
.
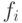Полной является система функций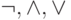 
. Законы 9 и 10 являются примерами, демонстрирующими, как импликация и тождество выражается через отрицание, конъюнкцию и дизъюнкцию.
Фактически полной является и система из двух функций – отрицания и конъюнкции или отрицания и дизъюнкции. Из законов де-Моргана следуют представления, позволяющие выразить конъюнкцию через отрицание и дизъюнкцию и соответственно выразить дизъюнкцию через отрицание и конъюнкцию:
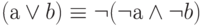
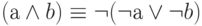
Парадоксально, но полной является система, состоящая всего из одной функции. Существуют две бинарные функции – антиконънкция и антидизъюнкция, называемые стрелкой Пирса и штрих Шеффера, представляющие полую систему.
В состав базовых функций языков программирования включают обычно тождество, отрицание, конъюнкцию и дизъюнкцию. В задачах ЕГЭ наряду с этими функциями часто встречается импликация.
Рассмотрим несколько простых задач, связанных с логическими функциями.
Задача 15:
Дан фрагмент таблицы истинности. Какая из трех приведенных функций соответствует этому фрагменту?
Ответ:
Функция под номером 3.
Решение:
Для решения задачи нужно знать таблицы истинности базовых функций и помнить о приоритетах операций. Напомню, что конъюнкция (логическое умножение) имеет более высокий приоритет и выполняется раньше, чем дизъюнкция (логическое сложение). При вычислениях нетрудно заметить, что функции с номерами 1 и 2 на третьем наборе имеют значение 1 и уже по этой причине фрагменту не соответствуют.
Задача 16:
Какое из приведенных чисел удовлетворяет условию:
(цифры, начиная со старшего разряда, идут в порядке убывания)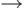 
(число - четное) 
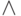(младшая цифра – четная) (старшая цифра – нечетная)
Если таких чисел несколько, укажите наибольшее.
- 13579
- 97531
- 24678
- 15386
Ответ:
Условию удовлетворяет число под номером 4.
Решение:
Первые два числа условию не удовлетворяют уже по той причине, что младшая цифра является нечетной. Конъюнкция условий ложна, если один из членов конъюнкции ложен. Для третьего числа не выполняется условие для старшей цифры. Для четвертого числа выполняются условия, накладываемые на младшую и старшую цифры числа. Первый член конъюнкции также истинен, поскольку импликация истинна, если ее посылка ложна, что имеет место в данном случае.
Задача 17: Два свидетеля дали следующие показания:
Первый свидетель: Если А виновен, то В и подавно виновен, а С – невиновен.
Второй свидетель: Виновны двое. А точно виновен и виновен один из оставшихся, но кто именно сказать не могу.
Какие заключения о виновности А, В и С можно сделать на основании свидетельских показаний?
Ответ: Из свидетельских показаний следует, что А и В виновны, а С – невиновен.
Решение: Конечно, ответ можно дать, основываясь на здравом смысле. Но давайте рассмотрим, как это можно сделать строго и формально.
Первое, что нужно сделать – это формализовать высказывания. Введем три логические переменные - А, В и С, каждая из которых имеет значение true (1), если соответствующий подозреваемый виновен. Тогда показания первого свидетеля задаются формулой:
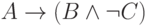
Показания второго свидетеля задаются формулой:
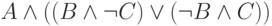
Показания обоих свидетелей полагаются истинными и представляют конъюнкцию соответствующих формул.
Построим таблицу истинности для этих показаний:
| A | B | C |  |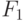
 |
 |
|---|---|---|---|---|---|
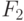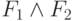| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 |
Суммарные свидетельские показания истинны только в одном случае, приводящие к однозначному ответу – А и В виновны, а С – невиновен.
Из анализа этой таблицы также следует, что показания второго свидетеля более информативны. Из истинности его показания следует только два возможных варианта - А и В виновны, а С – невиновен или А и С виновны, а В – невиновен. Показания первого свидетеля менее информативны – существует 5 различных вариантов, соответствующих его показаниям. Совместно показания обоих свидетелей дают однозначный ответ о виновности подозреваемых.
