Позиционные системы счисления. Представление целых чисел

Для записи целых чисел можно использовать разные способы. Такие способы принято называть системами счисления. Например, целое число можно записывать последовательностью "палочек". Число 5 выглядит при таком способе как |||||. Понятно, что такой способ хорош только для записи небольших чисел. Для записи целых чисел, особенно дат, иногда применяют римскую систему счисления. В этой системе 2013 год записывается следующим образом MMXIII.

Основным способом записи чисел является их запись в различных позиционных системах счисления. Для записи числа в позиционной системе счисления используется некоторое множество символов, называемых цифрами системы счисления. Общепринято использовать 10 цифр - 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, значения которых задают первые 10 чисел натурального ряда. Число используемых цифр задает основание системы счисления. В привычной со школьной скамьи десятичной системе счисления используются 10 цифр. В двоичной системе счисления с основанием 2 используются две цифры - 0 и 1. 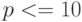В позиционных системах счисления с основанием , где обычно используются первые p из приведенных 10 цифр. В системах счисления с основанием десяти приведенных цифр не хватает, поэтому необходимы другие символы для записи цифр. В широко используемой при работе с компьютерами 16-иричной системе счисления, где необходимо 16 цифр, наряду с цифрами 0 - 9 в качестве цифр используют начальные буквы латинского алфавита - A, B, C, D, E, F, задающие соответственно числа от 10 до 15.

В любой системе счисления основание системы счисления – число – всегда записывается как число 10. Поясним причину этого на примере десятичной системы. Число 9 можно записать, используя цифру 9, но, если прибавить к 9 единицу, то на следующее число цифры уже не будет. Поэтому в позиционных системах в таких случаях число записывается с помощью двух цифр как число 10 – в младшем разряде пишется 0, а в старшем 1. В двоичной системе счисления числа 0 и 1 можно записать с помощью цифр, но, если прибавить к 1 единицу, то для двойки уже цифры нет, поэтому в двоичной системе число 2 записывается с помощью двух цифр, как число 10.

Вопрос: Чему равно число, записанное в системе счисления с основанием p как ?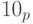

Ответ: Эта запись означает число p в привычной для нас десятичной системе счисления.

Вопрос: В каких системах счисления справедливы утверждения?

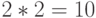
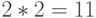
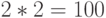
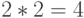
Ответы: ( В системах с основаниями соответственно: 4, 3, 2, в любых системах с основанием )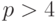

Рассмотрим привычную для нас запись числа 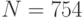в десятичной системе счисления. Не задумываясь, мы ответим, что число состоит из 7-и сотен, 5-и десятков и 4-х единиц.

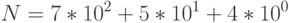
В общем случае запись 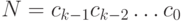, где 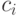– цифры системы счисления означает:

( *)

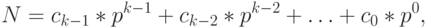где – основание системы счисления. Учитывая, что в любой системе счисления 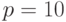, то справедлива и такая запись:

( **)

Вот точное определение:

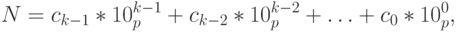Запись числа в позиционной системе счисления означает разложение числа по степеням основания. В роли коэффициентов выступают цифры системы счисления.

Понимание этого факта и соответствующего ему представления числа соотношением (*) достаточно для решения многих задач экзамена ЕГЭ.

Задача 1: Сколько единиц в двоичной записи числа 130?

Ответ: 2.

Решение. Число . Остальные коэффициенты равны 0. Полное решение задачи. Поскольку максимальная степень двойки равна 7, то число 130 в двоичной системе будет содержать 8 цифр – 2 единицы и 6 нулей

Задача 1 решается мгновенно, если помнить степени числа 2

Задача 2: Сколько нулей в троичной записи числа 130?

Ответ: 0

Решение: Используя разложение по степеням основания 3, число 130 можно представить:

Задача 2 может потребовать некоторых вычислений из-за того, что со степенями тройки сложнее работать, чем со степенями двойки, которые обычно помнит наизусть каждый ученик, изучающий информатику.

Задача 3: Чему равно число, записанное как 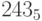в пятеричной системе счисления?

Ответ: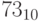

Решение: Это обратная задача по отношению к задаче 1. Здесь зная цифры и основание системы счисления нужно восстановить число, используя соотношение (*).

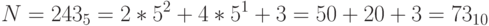
Задача 4: Число 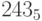записать в двоичной системе счисления?

Ответ:

Решение: Задача записи числа в системе счисления с основанием , если задана его запись в системе с основанием , решается в два этапа. На первом этапе число переводится в десятичную систему, на втором этапе – в систему с основанием .