|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Донецкий национальный технический университет
Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 6175 / 2305 | Оценка: 4.11 / 3.78 | Длительность: 12:32:00
Специальности: Математик
Лекция 10:
Моделирование многомерных нелинейных систем.
Определение матрицы Якоби
В методе Ньютона на каждом шаге итерационного процесса поиска необходимо формировать матрицу Якоби, при этом каждый элемент матрицы можно определить:
- аналитически, как частную производную
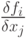 ,
, - методом численного дифференцирования, как отношение приращения функции к приращению аргумента, т.е.

В результате частная производная 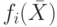 по первой координате х1 определится как
по первой координате х1 определится как
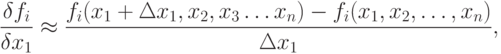
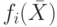 по координате хj определится как
по координате хj определится как
где 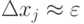 .
.
Метод Ньютона имеет преимущества по сравнению с другими методами. Но для метода Ньютона так же существует проблема сходимости, с увеличением числа неизвестных область сходимости уменьшается, а в случае больших систем, сходимость обеспечивается если начальная точка близка к искомому решению.
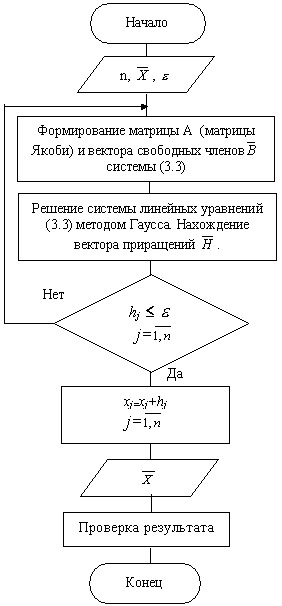
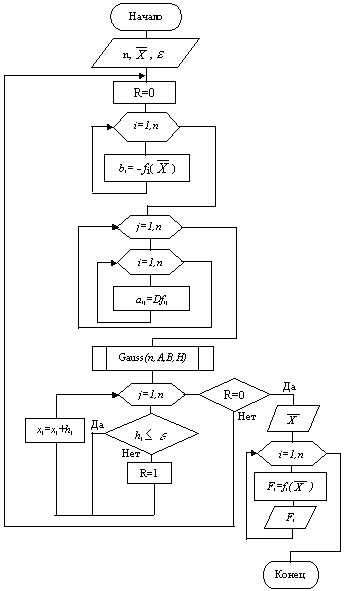
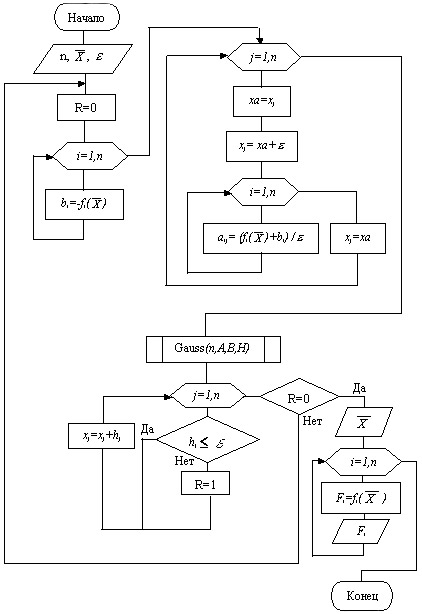
На рисунке 10.4 представлена укрупнённая схема алгоритма (блок-схема) метода Ньютона. На рисунках 10.5 и 10.6 представлены схемы алгоритмов метода Ньютона с различными способами определения матрицы Якоби.