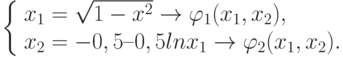Введение в математическое моделирование
[+]
Донецкий национальный технический университет
Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 5968 / 2125 | Оценка: 4.11 / 3.78 | Длительность: 12:32:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: алгоритмы, вычисления, графика, дискретная случайная величина, дифференциальные уравнения, законы, логика, многочлен, моделирование, нормальное распределение, нормальный закон, область сходимости, парабола, поиск, потоки, проектирование, разделенные разности, свободными членами, среднеквадратичное отклонение, теория, узловой
Лекция 10:

Моделирование многомерных нелинейных систем.
A
|
версия для печати
< Лекция 9 || Лекция 10: 1234 || Лекция 11 >

Рассмотрим пример.

Дана система нелинейных уравнений:

\left\{ \begin{array}{l} x_1^2 + x_2^2=1\\ lnx_1 + 2x_2= -1 \end{array} \right.

Необходимо определить область сходимости системы, выбрать начальную точку и найти одно из решений системы.

  1. Строим графики уравнений:

    Рис. 10.2.
  2. Преобразуем систему для решения методом итераций
    \left\{ \begin{array}{l} x_1=\sqrt{1-x^2}\to \varphi_1(x_1,x_2),\\ x_2=-0,5 – 0,5 ln x_1 \to \varphi_2(x_1,x_2). \end{array} \right.

Проверяем условие сходимости (10.4). Для заданной системы оно имеет вид:

\left| \delta \varphi_1 / \delta x_1\right| + \left| \delta \varphi_2 / \delta x_1\right|<1\\ \left| \delta \varphi_1 / \delta x_2\right| + \left| \delta \varphi_2 / \delta x_2\right|<1

Находим:

\delta \varphi_1 / \delta x_1=0;\\ \delta \varphi_1 / \delta x_2= -x / \sqrt{1-x_2};\\ \delta \varphi_2 / \delta x_1= -1/2x_1;\\ \delta \varphi_2 / \delta x_2= 0

В результате условие (10.4) будет иметь вид:

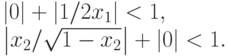
\left|0\right| + \left|1/2x_1\right|<1,\\ \left|x_2/\sqrt{1-x_2}\right| + \left|0\right|<1.

Определяем область сходимости G.

Граница области сходимости определится при решении системы,

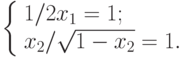
\left\{ \begin{array}{l} 1/2x_1=1;\\ x_2/\sqrt{1-x_2}=1. \end{array} \right.

Отсюда х1=0,5 ; x_2=\pm \sqrt 0,5.

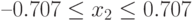В результате область сходимости определится при \left|x_1\right| \ge 0.5 и –0.707\le x_2\le 0.707.

На графике уравнений строим область сходимости G:


Рис. 10.3.

Выбираем начальную точку \overline{X^0}=[0.8; -0.6], принадлежащую области сходимости G. Используя выбранную начальную точку \overline{X^0}=[0.8; -0.6] решаем заданную систему нелинейных уравнений.

Дальше >>
< Лекция 9 || Лекция 10: 1234 || Лекция 11 >

Вопросы и ответы

вопросов: 4
Равиль Султанов
Равиль Султанов

В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "γ" (гамма).

P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа φ считается малым.

ответить
Александр Никитин
Александр Никитин

Добрый день.

В расчете параметра Т4 xi суммируется с величиной h/2 ?

ответить