НОУ ИНТУИТ | Введение в математическое моделирование. Лекция 10: Моделирование многомерных нелинейных систем.

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 6308 / 2328 | Оценка: 4.11 / 3.78 | Длительность: 12:32:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Решение систем нелинейных уравнений методом Ньютона

Дана система нелинейных уравнений

$\left\{ \begin{array}{l} f_1(x_1,x_2,x_3, \ldots, x_n)=0,\\ f_2(x_1,x_2,x_3, \ldots, x_n)=0,\\ \ldots \ldots \ldots \ldots \ldots\\ f_n(x_1,x_2,x_3, \ldots, x_n)=0, \end{array} \right.$

( 10.5)

или

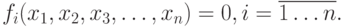
$f_i(x_1,x_2,x_3, \ldots, x_n)=0, i=\overline{1 \ldots n}.$

Необходимо решить эту систему, т.е. найти вектор $\bar X=[x_1,x_2,x_3,\ldots,x_n]$ , удовлетворяющий системе (10.5) с точностью $\varepsilon$ .

Метод Ньютона наиболее распространенный метод решения систем нелинейных уравнений. Он обеспечивает более быструю сходимость по сравнению с методом простых итераций.

В основе метода Ньютона лежит идея линеаризации всех нелинейных уравнений системы (10.5). Сообщим всей системе (10.5) малые приращения h_j и разложим каждое уравнение системы (10.5) в ряд Тейлора:

$\left\{ \begin{array}{l} f_1(x_1+h_1,x_2+h_2, \ldots, x_n+f_n)=f_1(x_1,x_2,\ldots,\x_n)+h_1 \frac{\delta f_1}{\delta x_1}+\\ + h_2 \frac{\delta f_1}{\delta x_2}+\ldots+ h_n \frac{\delta f_1}{\delta x_n}+R_1,\\ f_2(x_1+h_1,x_2+h_2, \ldots, x_n+f_n)=f_2(x_1,x_2,\ldots,\x_n)+h_1 \frac{\delta f_2}{\delta x_1}+\\ + h_2 \frac{\delta f_2}{\delta x_2}+\ldots+ h_n \frac{\delta f_2}{\delta x_n}+R_2,\\ \ldots \ldots \ldots \ldots \ldots \ldots\\ f_n(x_1+h_1,x_2+h_2, \ldots, x_n+f_n)=f_n(x_1,x_2,\ldots,\x_n)+h_1 \frac{\delta f_n}{\delta x_1}+\\ + h_2 \frac{\delta f_n}{\delta x_2}+\ldots+ h_n \frac{\delta f_n}{\delta x_n}+R_n, \end{array} \right.$

( 10.6)

где

h_j - приращение по каждой x_j;

R_i - остаточные нелинейные члены второго и более высоких порядков каждого ряда Тейлора.

Если приращения h_j таковы, что переменные x_j принимают значения близкие к корню, то будем считать, что левые части уравнений системы (10.6) обращаются в нули. Тогда отбросив R_i сведем задачу решения системы нелинейных уравнений (10.5) к решению системы линейных уравнений, в которой неизвестными являются приращения h_j, 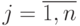$j=\overline{1,n}$

$\left\{ \begin{array}{l} h_1\frac{\delta f_1}{\delta x_1}+ h_2\frac{\delta f_1}{\delta x_2}+ \ldots + h_n\frac{\delta f_1}{\delta x_n}+R_1 = -f_1(x_1,x_2, \ldots,x_n),\\ h_1\frac{\delta f_2}{\delta x_1}+ h_2\frac{\delta f_2}{\delta x_2}+ \ldots + h_n\frac{\delta f_2}{\delta x_n}+R_2 = -f_2(x_1,x_2, \ldots,x_n),\\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots\\ h_1\frac{\delta f_n}{\delta x_1}+ h_2\frac{\delta f_n}{\delta x_2}+ \ldots + h_n\frac{\delta f_n}{\delta x_n}+R_n = -f_n(x_1,x_2, \ldots,x_n). \end{array} \right.$

( 10.7)

Система (10.7) – система линейных уравнений с неизвестными h_j, $j=\overline{1,n_j}$ . Запишем (10.7) в матричной форме

$A\cdot \bar H = \bar B,$

где

$A=\left[ \begin{array}{l} \frac{\delta f_1}{\delta x_1} \frac{\delta f_1}{\delta x_2} \cdots \frac{\delta f_1}{\delta x_n}\\ \frac{\delta f_2}{\delta x_1} \frac{\delta f_2}{\delta x_2} \cdots \frac{\delta f_2}{\delta x_n}\\ \ldots \ldots \ldots \ldots \\ \frac{\delta f_n}{\delta x_1} \frac{\delta f_n}{\delta x_2} \cdots \frac{\delta f_n}{\delta x_n} \end{array} \right] \text{ – матрица коэффициентов системы},$

( 10.8)

$\bar B=\left[ \begin{array}{l} -f_1\\ -f_2\\ \ldots \\ -f_n \end{array} \right] \text{ – вектор свободных членов},$

$\bar H=\left[ \begin{array}{l} h_1\\ h_2\\ \ldots \\ h_n \end{array} \right] \text{ – вектор неизвестных системы}.$

( 10.9)

Матрица А, составленая из частных производных $a_{ij}=\frac{\delta f_i}{\delta x_j}; i=\overline{1,n}; j=\overline{1,n}$ ; называется матрицей Якоби или Якобианом.

Метод Ньютона состоит из двух этапов:

На первом этапе реализации метода Ньютона необходимо построить систему (10.3).

На втором этапе, начиная с начальной точки 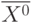$\overline{X^0}$ , необходимо решать систему (10.7) на каждом шаге итерационного процесса поиска методом Гаусса. Найденные значения приращений h_j используются как поправки к решению, полученному на предыдущем шаге поиска, т.е.