Базовые понятия теории информации
Информация - нематериальная сущность, при помощи которой с любой точностью можно описывать реальные (материальные), виртуальные (возможные) и понятийные сущности. Информация - противоположность неопределенности.
Канал связи - это среда передачи информации, которая характеризуется в первую очередь максимально возможной для нее скоростью передачи данных ( емкостью канала связи).
Шум - это помехи в канале связи при передаче информации.
Кодирование - преобразование дискретной информации одним из следующих способов: шифрование, сжатие, защита от шума.
Общая схема передачи информации изображена на рис.2.1.
Емкость канала связи без шума можно приблизительно вычислить, зная максимальную частоту волновых процессов, допустимую в этом канале. Можно считать, что скорость передачи данных может быть не меньше, чем эта частота. Например, при предельной частоте, равной 1000Гц, можно обеспечить скорость передачи данных не меньше 1Кбод.
Примеры каналов связи и связанных с ними предельных частот: телеграф - 140Гц, телефон - до 3.1КГц, короткие волны (10-100м) - 3-30МГц, УКВ (1-10м) - 30-300МГц, спутник (сантиметровые волны) - до 30ГГц, оптический (инфракрасный диапазон) - 0.15-400ТГц, оптический (видимый свет) - 400-700ТГц, оптический (ультрафиолетовый диапазон) - 0.7-1.75ПГц.
Типичные современные каналы: телеграфный и телефонный. Перспективные, внедряемые ныне: оптоволоконный (терабоды) и цифровой телефонный (ISDN, Integrated Services Digital Networks) - 57-128 Кбод.
В реальных оптоволоконных системах скорость гораздо ниже теоретических пределов (редко превосходит 1-10Гбод).
Наиболее широко пока используются телефонные линии связи. Здесь достигнута скорость более 50 Кбод!
Способы измерения информации
Понятие количества информации естественно возникает, например, в следующих типовых случаях:
- Равенство вещественных переменных
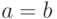 , заключает в себе
информацию о том, что
, заключает в себе
информацию о том, что  равно
равно  . Про равенство
. Про равенство  можно сказать, что оно несет меньшую информацию, чем первое, т.к. из первого
следует второе, но не наоборот. Равенство
можно сказать, что оно несет меньшую информацию, чем первое, т.к. из первого
следует второе, но не наоборот. Равенство  несет в себе
информацию по объему такую же, как и первое;
несет в себе
информацию по объему такую же, как и первое; - Пусть происходят некоторые измерения с некоторой погрешностью. Тогда чем больше будет проведено измерений, тем больше информации об измеряемой сущности будет получено;
- Математическое ожидание некоторой случайной величины, содержит в себе информацию о самой случайной величине, Для случайной величины, распределенной по нормальному закону, с известной дисперсией знание математического ожидания дает полную информацию о случайной величине;
- Рассмотрим схему передачи информации. Пусть передатчик
описывается случайной величиной,
 , тогда из-за помех в канале связи на
приемник будет приходить случайная величина,
, тогда из-за помех в канале связи на
приемник будет приходить случайная величина, 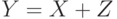 , где
, где  - это случайная величина, описывающая помехи.
В этой схеме можно говорить о количестве информации, содержащейся в случайной величине,
- это случайная величина, описывающая помехи.
В этой схеме можно говорить о количестве информации, содержащейся в случайной величине,  ,
относительно
,
относительно  . Чем ниже уровень помех (дисперсия
. Чем ниже уровень помех (дисперсия  мала), тем
больше информации можно получить из
мала), тем
больше информации можно получить из  . При отсутствии помех
. При отсутствии помех  содержит в
себе всю информацию об
содержит в
себе всю информацию об  .
.
В 1865 г. немецкий физик Рудольф Клаузиус ввел в статистическую физику понятие энтропии или меры уравновешенности системы.
В 1921 г. основатель большей части математической статистики, англичанин Роналд Фишер впервые ввел термин "информация" в математику, но полученные им формулы носят очень специальный характер.
В 1948 г. Клод Шеннон в своих работах по теории связи выписывает формулы для вычисления количества информации и энтропии. Термин энтропия используется Шенноном по совету патриарха компьютерной эры фон Неймана, отметившего, что полученные Шенноном для теории связи формулы для ее расчета совпали с соответствующими формулами статистической физики, а также то, что "точно никто не знает" что же такое энтропия.
Упражнение 4
Какое из соотношений несет в себе больше информации 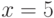 или
или  ?
?

