Сжатие информации
Цель сжатия - уменьшение количества бит, необходимых для хранения или передачи заданной информации, что дает возможность передавать сообщения более быстро и хранить более экономно и оперативно (последнее означает, что операция извлечения данной информации с устройства ее хранения будет проходить быстрее, что возможно, если скорость распаковки данных выше скорости считывания данных с носителя информации). Сжатие позволяет, например, записать больше информации на дискету, "увеличить" размер жесткого диска, ускорить работу с модемом и т.д. При работе с компьютерами широко используются программы-архиваторы данных формата ZIP, GZ, ARJ и других. Методы сжатия информации были разработаны как математическая теория, которая долгое время (до первой половины 80-х годов), мало использовалась в компьютерах на практике.
Сжатие данных не может быть большим некоторого теоретического предела.
Для формального определения этого предела рассматриваем любое информационное
сообщение длины  как последовательность независимых, одинаково
распределенных д.с.в.
как последовательность независимых, одинаково
распределенных д.с.в. 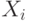 или как выборки длины
или как выборки длины  значений одной д.с.в.
значений одной д.с.в.  .
.
Доказано120
, что среднее количество бит, приходящихся на одно
кодируемое значение д.с.в., не может быть меньшим, чем энтропия
этой д.с.в., т.е. 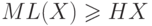 для любой д.с.в.
для любой д.с.в.  и
любого ее кода.
и
любого ее кода.
Кроме того, Доказано220
утверждение о том, что существует такое
кодирование (Шеннона-Фэно, Fano), что 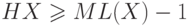 .
.
Рассмотрим д.с.в. 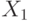 и
и 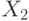 , независимые и
одинаково распределенные.
, независимые и
одинаково распределенные.  и
и 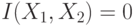 , следовательно,
, следовательно,
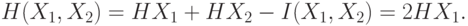
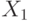 и
и 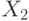 можно говорить о двумерной
д.с.в.
можно говорить о двумерной
д.с.в.  . Аналогичным образом для
. Аналогичным образом для  -мерной д.с.в.
-мерной д.с.в. 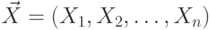 можно получить, что
можно получить, что 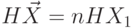 .
.Пусть 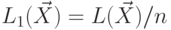 , где
, где 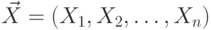 , т.е.
, т.е.  - это количество бит кода на единицу
сообщения
- это количество бит кода на единицу
сообщения  . Тогда
. Тогда 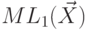 - это среднее
количество бит кода на единицу сообщения при передаче бесконечного множества сообщений
- это среднее
количество бит кода на единицу сообщения при передаче бесконечного множества сообщений  . Из
. Из  для кода Шеннона-Фэно
для
для кода Шеннона-Фэно
для  следует
следует 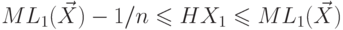 для этого же кода.
для этого же кода.
Таким образом, доказана основная теорема о кодировании при отсутствии помех, а именно то, что с
ростом длины  сообщения, при кодировании методом Шеннона-Фэно всего сообщения
целиком среднее количество бит на единицу
сообщения будет сколь угодно мало отличаться от энтропии единицы
сообщения. Подобное кодирование практически не реализуемо из-за того, что
с ростом длины сообщения трудоемкость построения этого кода становится
недопустимо большой. Кроме того, такое кодирование делает невозможным
отправку сообщения по частям, что необходимо для непрерывных процессов
передачи данных. Дополнительным недостатком этого способа кодирования является
необходимость отправки или хранения собственно полученного кода вместе с
его исходной длиной, что снижает эффект от сжатия. На практике для повышения
степени сжатия используют метод блокирования.
сообщения, при кодировании методом Шеннона-Фэно всего сообщения
целиком среднее количество бит на единицу
сообщения будет сколь угодно мало отличаться от энтропии единицы
сообщения. Подобное кодирование практически не реализуемо из-за того, что
с ростом длины сообщения трудоемкость построения этого кода становится
недопустимо большой. Кроме того, такое кодирование делает невозможным
отправку сообщения по частям, что необходимо для непрерывных процессов
передачи данных. Дополнительным недостатком этого способа кодирования является
необходимость отправки или хранения собственно полученного кода вместе с
его исходной длиной, что снижает эффект от сжатия. На практике для повышения
степени сжатия используют метод блокирования.
По выбранному значению 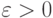 можно выбрать такое
можно выбрать такое  , что если
разбить все сообщение на блоки длиной
, что если
разбить все сообщение на блоки длиной  (всего будет
(всего будет 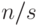 блоков), то
кодированием Шеннона-Фэно таких блоков, рассматриваемых как единицы сообщения,
можно сделать среднее количество бит на единицу сообщения большим энтропии
менее, чем на
блоков), то
кодированием Шеннона-Фэно таких блоков, рассматриваемых как единицы сообщения,
можно сделать среднее количество бит на единицу сообщения большим энтропии
менее, чем на  . Действительно, пусть
. Действительно, пусть  ,
, 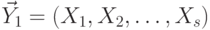 ,
, 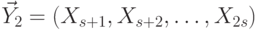 и т.д., т.е.
и т.д., т.е. 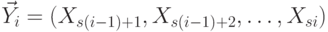 . Тогда
. Тогда 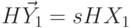 и
и 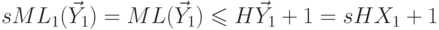 ,
следовательно,
,
следовательно,
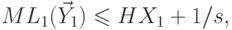
 .
Минимум
.
Минимум  по заданному
по заданному  может быть
гораздо меньшим
может быть
гораздо меньшим 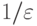 .
.Пример. Пусть д.с.в. 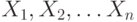 независимы, одинаково
распределены
и могут принимать только два значения
независимы, одинаково
распределены
и могут принимать только два значения  и
и 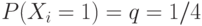 при
при  от 1 до
от 1 до  . Тогда
. Тогда

 -
-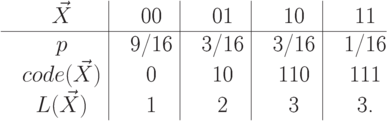
Тогда при таком минимальном кодировании количество бит в среднем на единицу сообщения будет уже
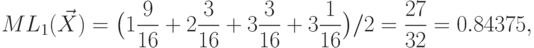
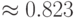 , для блоков длины 4 -
, для блоков длины 4 -  и
т.д.
и
т.д.Все изложенное ранее подразумевало, что рассматриваемые д.с.в.
кодируются только двумя значениями (обычно 0 и 1). Пусть д.с.в.
кодируются  значениями. Тогда для д.с.в.
значениями. Тогда для д.с.в.  и
любого ее кодирования верно, что
и
любого ее кодирования верно, что 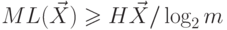 и
и 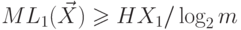 . Кроме того,
существует кодирование такое, что
. Кроме того,
существует кодирование такое, что 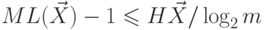 и
и 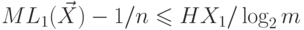 , где
, где  .
.
Формулы теоретических пределов уровня сжатия, рассмотренные ранее, задают предел для средней длины кода на единицу сообщений, передаваемых много раз, т.е. они ничего не говорят о нижней границе уровня сжатия, которая может достигаться на некоторых сообщениях и быть меньшей энтропии д.с.в., реализующей сообщение.
