Математическая модель системы связи
Коды делятся на два больших класса. Коды с исправлением ошибок имеют целью восстановить с вероятностью, близкой к единице, посланное сообщение. Коды с обнаружением ошибок имеют целью выявить с вероятностью, близкой к единице, наличие ошибок.
Простой код с обнаружением ошибок основан на схеме проверки
четности,
применимой к сообщениям 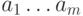 любой фиксированной длины
любой фиксированной длины  . Схема кодирования определяется следующими формулами:
. Схема кодирования определяется следующими формулами: 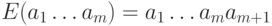 ,
,
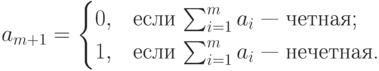
 должна быть четной.
должна быть четной.Соответствующая схема декодирования тривиальна:
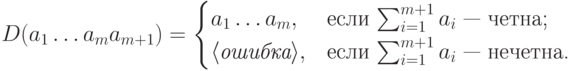
 не гарантирует
безошибочной передачи.
не гарантирует
безошибочной передачи.Пример. Проверка четности при  реализуется следующим кодом
(функцией
реализуется следующим кодом
(функцией  ):
):  ,
,  ,
,  ,
,  . В двоичном симметричном
канале доля неверно принятых сообщений для этого
кода (хотя бы с одной ошибкой) равна
. В двоичном симметричном
канале доля неверно принятых сообщений для этого
кода (хотя бы с одной ошибкой) равна 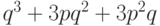 (три, две
или одна ошибка соответственно). Из них незамеченными окажутся только ошибки точно в
двух битах, не изменяющие четности. Вероятность таких ошибок
(три, две
или одна ошибка соответственно). Из них незамеченными окажутся только ошибки точно в
двух битах, не изменяющие четности. Вероятность таких ошибок 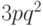 .
Вероятность ошибочной передачи сообщения из двух бит равна
.
Вероятность ошибочной передачи сообщения из двух бит равна 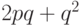 .
При малых
.
При малых  верно, что
верно, что 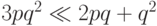 .
.
Рассмотрим 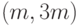 -код с тройным повторением.
Коды с повторениями очень неэффективны, но полезны в качестве теоретического примера кодов,
исправляющих ошибки. Любое сообщение разбивается на блоки длиной
-код с тройным повторением.
Коды с повторениями очень неэффективны, но полезны в качестве теоретического примера кодов,
исправляющих ошибки. Любое сообщение разбивается на блоки длиной  каждое и каждый блок передается трижды - это определяет функцию
каждое и каждый блок передается трижды - это определяет функцию  .
Функция
.
Функция  определяется следующим образом. Принятая строка разбивается на блоки длиной
определяется следующим образом. Принятая строка разбивается на блоки длиной  . Бит с номером
. Бит с номером 
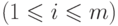 в
декодированном блоке получается из анализа битов с номерами
в
декодированном блоке получается из анализа битов с номерами  ,
, 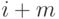 ,
, 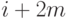 в полученном блоке: берется
тот бит из трех, который встречается не менее двух раз. Вероятность того,
что бит в данной позиции будет принят трижды правильно равна
в полученном блоке: берется
тот бит из трех, который встречается не менее двух раз. Вероятность того,
что бит в данной позиции будет принят трижды правильно равна 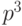 .
Вероятность одной ошибки в тройке равна
.
Вероятность одной ошибки в тройке равна 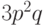 . Поэтому
вероятность правильного приема одного бита равна
. Поэтому
вероятность правильного приема одного бита равна 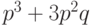 . Аналогичным
образом получается, что вероятность приема ошибочного бита равна
. Аналогичным
образом получается, что вероятность приема ошибочного бита равна 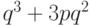 .
.
Пример. Предположим 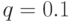 . Тогда вероятность ошибки при
передачи одного бита - 0.028, те. этот код снижает вероятность ошибки с 10% до 2.8%.
Подобным образом организованная передача с пятикратным повторением даст
вероятность ошибки на бит
. Тогда вероятность ошибки при
передачи одного бита - 0.028, те. этот код снижает вероятность ошибки с 10% до 2.8%.
Подобным образом организованная передача с пятикратным повторением даст
вероятность ошибки на бит 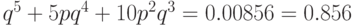 , т.е.
менее 1%. В результате вероятность правильной передачи строки длиной 10
возрастет с
, т.е.
менее 1%. В результате вероятность правильной передачи строки длиной 10
возрастет с 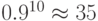 до
до  при тройных
повторениях и до
при тройных
повторениях и до 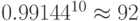 при пятикратных
повторениях.
при пятикратных
повторениях.
Тройное повторение обеспечивает исправление одной ошибки в каждой позиции за счет трехкратного увеличения времени передачи.
Рассмотрим 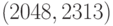 -код, используемый при записи данных на
магнитофонную ленту компьютерами Apple II. К каждому байту исходных данных прибавляется бит
четности и, кроме того, после каждых таких расширенных битом четности 256
байт добавляется специальный байт, также расширенный битом четности. Этот
специальный байт, который называют контрольной суммой (check sum),
есть результат применения поразрядной логической операции "исключающее
ИЛИ" (XOR) к 256 предшествующим расширенным байтам. Этот код
способен как обнаруживать ошибки нечетной кратности в каждом из отдельных
байт, так и исправлять до 8 ошибок в блоке длиной 256 байт. Исправление
ошибок основано на том, что если в одном из бит одного из байт 256 байтового
блока произойдет сбой, обнаруживаемый проверкой четности, то этот же сбой
проявится и в том, что результат операции "исключающее ИЛИ" над всеми
соответствующими битами блока не будет соответствовать
соответствующему биту контрольной суммы. Сбойный бит однозначно определяется
пересечением сбойных колонки байта и строки бита контрольной суммы.
На
рис.
8.1 изображена схема участка ленты, содержащего ровно 9 ошибок в
позициях, обозначенных
-код, используемый при записи данных на
магнитофонную ленту компьютерами Apple II. К каждому байту исходных данных прибавляется бит
четности и, кроме того, после каждых таких расширенных битом четности 256
байт добавляется специальный байт, также расширенный битом четности. Этот
специальный байт, который называют контрольной суммой (check sum),
есть результат применения поразрядной логической операции "исключающее
ИЛИ" (XOR) к 256 предшествующим расширенным байтам. Этот код
способен как обнаруживать ошибки нечетной кратности в каждом из отдельных
байт, так и исправлять до 8 ошибок в блоке длиной 256 байт. Исправление
ошибок основано на том, что если в одном из бит одного из байт 256 байтового
блока произойдет сбой, обнаруживаемый проверкой четности, то этот же сбой
проявится и в том, что результат операции "исключающее ИЛИ" над всеми
соответствующими битами блока не будет соответствовать
соответствующему биту контрольной суммы. Сбойный бит однозначно определяется
пересечением сбойных колонки байта и строки бита контрольной суммы.
На
рис.
8.1 изображена схема участка ленты, содержащего ровно 9 ошибок в
позициях, обозначенных 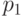 ,
, 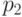 ,
,  ,
, 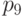 . Расширенный байт
контрольной суммы обозначен CS, а бит паритета (в данном случае четности) -
PB (parity bit). Ошибка в позиции
. Расширенный байт
контрольной суммы обозначен CS, а бит паритета (в данном случае четности) -
PB (parity bit). Ошибка в позиции 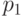 может быть исправлена.
Ошибки в позициях
может быть исправлена.
Ошибки в позициях 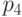 ,
, 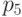 ,
,  ,
, 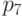 можно обнаружить, но не исправить. Ошибки
в позициях
можно обнаружить, но не исправить. Ошибки
в позициях 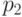 ,
, 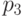 ,
, 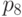 ,
, 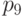 невозможно даже обнаружить.
невозможно даже обнаружить.
Приведенные ранее примеры простейших кодов принадлежат к классу блочных.
По определению, блочный код заменяет каждый блок из  символов более
длинным блоком из
символов более
длинным блоком из  символов. Следовательно,
символов. Следовательно, 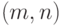 -коды являются блочными.
Существуют также древовидные
или последовательные коды,
в которых значение очередного контрольного символа зависит от всего
предшествующего фрагмента сообщения. Работа с древовидным шумозащитным кодом
имеет сходство с работой с арифметическим кодом для сжатия информации.
-коды являются блочными.
Существуют также древовидные
или последовательные коды,
в которых значение очередного контрольного символа зависит от всего
предшествующего фрагмента сообщения. Работа с древовидным шумозащитным кодом
имеет сходство с работой с арифметическим кодом для сжатия информации.
Расстоянием (Хэмминга) между двоичными словами
длины  называется количество позиций, в которых эти слова
различаются.
Это одно из ключевых понятий теории кодирования. Если обозначить двоичные
слова как
называется количество позиций, в которых эти слова
различаются.
Это одно из ключевых понятий теории кодирования. Если обозначить двоичные
слова как 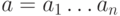 и
и 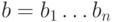 , то
расстояние между ними
обозначается
, то
расстояние между ними
обозначается 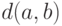 .
.
Весом двоичного
слова 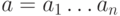 называется количество единиц в нем. Обозначение
называется количество единиц в нем. Обозначение  .
Можно сказать, что
.
Можно сказать, что  .
.

