Математическая модель системы связи
Пример. Пусть 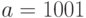 и
и 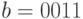 , тогда
, тогда 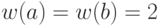 ,
, 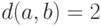 .
.
Далее операция 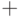 при применении к двоичным словам будет
означать
поразрядное сложение без переноса, т.е. сложение по модулю 2 или
"исключающее ИЛИ" (XOR).
при применении к двоичным словам будет
означать
поразрядное сложение без переноса, т.е. сложение по модулю 2 или
"исключающее ИЛИ" (XOR).
Расстояние между двоичными словами  и
и  равно
весу их поразрядной суммы,
т.е.
равно
весу их поразрядной суммы,
т.е. 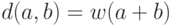 .
.
Если два слова различаются в каком-либо разряде, то это добавит единицу к весу их поразрядной суммы.
Следовательно, если  и
и  - слова длины
- слова длины  , то
вероятность того, что слово
, то
вероятность того, что слово  будет принято как
будет принято как  ,
равна
,
равна 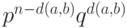 .
.
Наример, вероятность того, что слово 1011 будет принято как 0011, равна 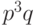 .
.
Для возможности обнаружения ошибки в одной позиции минимальное расстояние между словами кода должно быть большим 1.
Иначе ошибка в одной позиции сможет превратить одно кодовое слово в другое, что не даст ее обнаружить.
Для того, чтобы код давал возможность обнаруживать все ошибки
кратности, не большей  , необходимо и достаточно, чтобы
наименьшее расстояние между его словами было
, необходимо и достаточно, чтобы
наименьшее расстояние между его словами было  .
.
Достаточность доказывается конструктивно: если условие
утверждения выполнено для  , то в качестве декодирующей функции
, то в качестве декодирующей функции  следует взять функцию, сообщающую об ошибке, если декодируемое слово
отличается от любого из слов из образа
следует взять функцию, сообщающую об ошибке, если декодируемое слово
отличается от любого из слов из образа  . Необходимость
доказывается от противного: если минимальное расстояние
. Необходимость
доказывается от противного: если минимальное расстояние 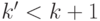 , то ошибка в
, то ошибка в 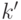 позициях сможет превратить одно кодовое слово в другое.
позициях сможет превратить одно кодовое слово в другое.
Для такого кода вероятность того, что ошибки в сообщении останутся необнаруженными, равна
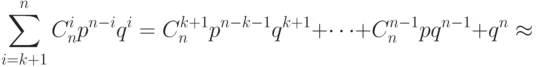
 при малых
при малых  и не слишком маленьких
и не слишком маленьких ![k]\approx C^{k+1}_np^{n-k-1}q^{k+1}](/sites/default/files/tex_cache/3792aef14b7dacb9b680d466cb130930.png) .
.Для того, чтобы код давал возможность исправлять все ошибки кратности, не
большей  , необходимо и достаточно, чтобы наименьшее расстояние
между его словами было
, необходимо и достаточно, чтобы наименьшее расстояние
между его словами было 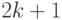 .
.
Достаточность доказывается конструктивно: если условие утверждения
выполнено для  , то в качестве декодирующей функции
, то в качестве декодирующей функции  следует взять функцию, возвращающую ближайшее к декодируемому слово из образа
следует взять функцию, возвращающую ближайшее к декодируемому слово из образа  . Необходимость доказывается от противного. Пусть расстояние
между выбранными словами в коде равно
. Необходимость доказывается от противного. Пусть расстояние
между выбранными словами в коде равно 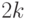 . Тогда если при передаче
каждого из этих слов случится
. Тогда если при передаче
каждого из этих слов случится  ошибок, которые изменят биты, в которых
различаются эти слова, то приемник получит два идентичных сообщения, что
свидетельствует о том, что в данной ситуации исправление
ошибок, которые изменят биты, в которых
различаются эти слова, то приемник получит два идентичных сообщения, что
свидетельствует о том, что в данной ситуации исправление  ошибок
невозможно. Следовательно, минимальное расстояние между словами кода должно
быть большим
ошибок
невозможно. Следовательно, минимальное расстояние между словами кода должно
быть большим 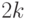 .
.
Пример. Рассмотрим 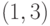 -код, состоящий из
-код, состоящий из  ,
задающей отображение
,
задающей отображение 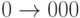 и
и 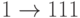 , и
, и  ,
задающей отображение
,
задающей отображение 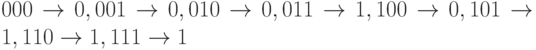 .
Этот код (с тройным повторением) исправляет ошибки в одной позиции, т.к. минимальное
расстояние между словами кода равно 3.
.
Этот код (с тройным повторением) исправляет ошибки в одной позиции, т.к. минимальное
расстояние между словами кода равно 3.
Если код исправляет все ошибки кратности  и меньшей, то
вероятность ошибочного приема слова длины
и меньшей, то
вероятность ошибочного приема слова длины  очевидно не превосходит
очевидно не превосходит 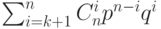 . Вероятность правильного приема в
этом случае не меньше, чем
. Вероятность правильного приема в
этом случае не меньше, чем
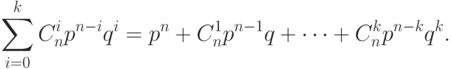
Передачу данных часто удобно рассматривать следующим образом. Исходное
сообщение 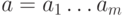 кодируется функцией
кодируется функцией  в
кодовое слово
в
кодовое слово 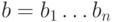 . Канал связи при передаче добавляет к нему
функцией
. Канал связи при передаче добавляет к нему
функцией  строку ошибок
строку ошибок 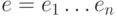 так, что приемник получает сообщение
так, что приемник получает сообщение 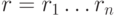 ,
где
,
где 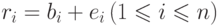 . Система, исправляющая
ошибки, переводит
. Система, исправляющая
ошибки, переводит  в некоторое (обычно ближайшее) кодовое слово.
Система, только обнаруживающая ошибки, лишь проверяет, является ли принятое
слово кодовым, и сигнализирует о наличии ошибки, если это не так.
в некоторое (обычно ближайшее) кодовое слово.
Система, только обнаруживающая ошибки, лишь проверяет, является ли принятое
слово кодовым, и сигнализирует о наличии ошибки, если это не так.
Пример. Пусть передаваемое слово 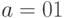 кодируется словом
кодируется словом 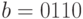 , а строка
ошибок -
, а строка
ошибок - 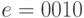 . Тогда будет принято слово
. Тогда будет принято слово 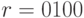 .
Система, исправляющая ошибки, переведет его в 0110 и затем восстановит переданное
слово 01.
.
Система, исправляющая ошибки, переведет его в 0110 и затем восстановит переданное
слово 01.
Если система только обнаруживает ошибки и расстояние между любыми кодовыми
словами 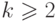 , то любая строка ошибок
, то любая строка ошибок  с
единственной единицей приведет к слову
с
единственной единицей приведет к слову 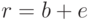 , которое не является кодовым.
, которое не является кодовым.
Пример. Рассмотрим 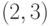 -код с проверкой четности. Множество
кодовых слов -
-код с проверкой четности. Множество
кодовых слов - 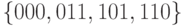 . Ни одна из строк ошибок 001, 010,
100, 111 не переводит одно кодовое слово в другое. Поэтому однократная и тройная ошибки
могут быть обнаружены.
. Ни одна из строк ошибок 001, 010,
100, 111 не переводит одно кодовое слово в другое. Поэтому однократная и тройная ошибки
могут быть обнаружены.
Пример. Следующий 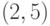 -код обнаруживает две ошибки:
-код обнаруживает две ошибки:


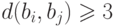 при
при  , следует, что однократная
ошибка приведет к приему слова, которое находится на расстоянии 1 от кодового
слова, которое было передано. Поэтому схема декодирования, состоящая в том,
что принятое слово переводится в ближайшее к нему кодовое, будет исправлять
однократную ошибку. В двоичном симметричном канале вероятность правильной
передачи одного блока будет не меньше чем
, следует, что однократная
ошибка приведет к приему слова, которое находится на расстоянии 1 от кодового
слова, которое было передано. Поэтому схема декодирования, состоящая в том,
что принятое слово переводится в ближайшее к нему кодовое, будет исправлять
однократную ошибку. В двоичном симметричном канале вероятность правильной
передачи одного блока будет не меньше чем 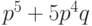 .
.Установлено 120 , что в 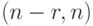 -коде, минимальное
расстояние между кодовыми словами которого
-коде, минимальное
расстояние между кодовыми словами которого 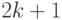 , числа
, числа  ,
,  (число дополнительных разрядов в кодовых словах) и
(число дополнительных разрядов в кодовых словах) и  должны соответствовать неравенству
должны соответствовать неравенству
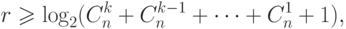
 ,
,  и
и  соответствуют неравенству
соответствуют неравенству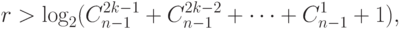
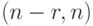 -код,
исправляющий все ошибки веса
-код,
исправляющий все ошибки веса  и менее220 .
и менее220 .Нижняя граница задает необходимое условие для помехозащитного кода с заданными характеристиками, т.е. любой такой код должен ему соответствовать, но не всегда можно построить код по подобранным, удовлетворяющим условию характеристикам. Верхняя граница задает достаточное условие для существования помехозащитного кода с заданными характеристиками, т.е. по любым подобранным, удовлетворяющим условию характеристикам можно построить им соответствующий код.
Упражнение 37
Имеется 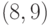 -код с проверкой четности. Вычислить вероятность
того, что в случае ошибки этот код ее не обнаружит, если вероятность ошибки при
передаче каждого бита равна 1%. Вычислить также вероятность
ошибочной передачи без использования кода. Сделать аналогичные расчеты для
случая, когда вероятность ошибки в десять раз меньше.
-код с проверкой четности. Вычислить вероятность
того, что в случае ошибки этот код ее не обнаружит, если вероятность ошибки при
передаче каждого бита равна 1%. Вычислить также вероятность
ошибочной передачи без использования кода. Сделать аналогичные расчеты для
случая, когда вероятность ошибки в десять раз меньше.
Упражнение 38
Вычислить минимальную и максимальную оценки количества дополнительных
разрядов  для кодовых слов длины
для кодовых слов длины  , если требуется,
чтобы минимальное расстояние между ними было
, если требуется,
чтобы минимальное расстояние между ними было  . Рассмотреть случаи
. Рассмотреть случаи 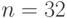 ,
,  и
и 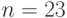 ,
, 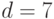 .
.
