Ультрафильтры и компактность
165. Покажите, что для счетного объединения аналогичное утверждение
может не быть верным и 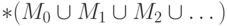 может отличаться от
может отличаться от 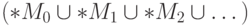 .
.
Нестандартные аналоги имеют не только множества, но и функции. Мы уже говорили о нестандартном аналоге синуса. Точно так же можно определить нестандартный аналог любой всюду определенной функции (любого числа аргументов). Для не всюду определенных функций (например, для функции квадратного корня) надо рассмотреть ее график как предикат (для корня это будет предикат двух аргументов) и взять его нестандартный аналог. Этот нестандартный аналог будет графиком частичной функции (ибо свойство "быть графиком частичной функции" записывается формулой). Соответствующая функция и будет нестандартным аналогом исходной.
166. Покажите, что (построенный по этой схеме) нестандартный
квадратный корень имеет областью определения множество
неотрицательных гипердействительных чисел и что 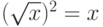 для любого неотрицательного
гипердействительного числа
для любого неотрицательного
гипердействительного числа  .
.
167. Покажите, что для всюду определенной функции два способа ее продолжения (как функции и через график) дают одну и ту же функцию.
168. Покажите, что если множество  является областью определения
частичной функции
является областью определения
частичной функции  , то его нестандартный аналог
, то его нестандартный аналог 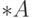 совпадает с областью определения функции
совпадает с областью определения функции 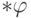 .
.
Мы будем часто опускать звездочки в записях вида 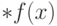 ,
пользуясь таким соглашением: если речь идет о значении функции
на гипердействительном числе, то подразумевается нестандартный
аналог этой функции. (Путаницы не будет, так как на стандартных
числах значения функции и ее гипердействительного аналога
совпадают.)
,
пользуясь таким соглашением: если речь идет о значении функции
на гипердействительном числе, то подразумевается нестандартный
аналог этой функции. (Путаницы не будет, так как на стандартных
числах значения функции и ее гипердействительного аналога
совпадают.)
169. Абсолютную величину гипердействительного числа  можно определить
как
можно определить
как  при
при  и как
и как 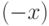 при
при  . С другой стороны, можно рассмотреть нестандартный аналог
функции
. С другой стороны, можно рассмотреть нестандартный аналог
функции 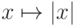 . Покажите, что получится одно и то же.
. Покажите, что получится одно и то же.
170. Покажите, что поле гипердействительных чисел является вещественно замкнутым.
Любое гипердействительное число  можно представить в виде
суммы гиперцелого числа
можно представить в виде
суммы гиперцелого числа  и некоторого гипердействительного
числа
и некоторого гипердействительного
числа  , для которого
, для которого 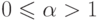 . Чтобы
убедиться в этом, достаточно рассмотреть нестандартные аналоги
функций целой и дробной части. Принцип переноса гарантирует, что
они сохранят свои свойства. В частности, в сумме они дают
исходное число, а дробная часть всегда не меньше нуля и меньше
единицы.
. Чтобы
убедиться в этом, достаточно рассмотреть нестандартные аналоги
функций целой и дробной части. Принцип переноса гарантирует, что
они сохранят свои свойства. В частности, в сумме они дают
исходное число, а дробная часть всегда не меньше нуля и меньше
единицы.
Целью расширения было получить возможность рассматривать бесконечно большие и бесконечно малые числа. Дадим соответствующие определения.
Гипердействительное число  , большее всех стандартных
чисел, называется положительным бесконечно большим.
Аналогично определяются отрицательные бесконечно большие числа.
, большее всех стандартных
чисел, называется положительным бесконечно большим.
Аналогично определяются отрицательные бесконечно большие числа.
171. Докажите, что число  является отрицательным бесконечно большим
тогда и только тогда, когда
является отрицательным бесконечно большим
тогда и только тогда, когда  является положительным
бесконечно большим. Докажите, что
является положительным
бесконечно большим. Докажите, что 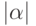 является положительным бесконечно
большим тогда и только тогда, когда
является положительным бесконечно
большим тогда и только тогда, когда  является либо
положительным, либо отрицательным бесконечно большим.
является либо
положительным, либо отрицательным бесконечно большим.
Гипердействительные числа, не являющиеся бесконечно большими,
называют конечными. Другими словами, гипердействительное
число  называется конечным,
если оно лежит в промежутке
называется конечным,
если оно лежит в промежутке 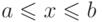 со стандартными концами
со стандартными концами  и
и  .
.
Наконец, гипердействительное число называется бесконечно
малым, если его абсолютная величина меньше любого стандартного
положительного числа. (Согласно этому определению нуль тоже
является бесконечно малым числом.) Легко проверить, что
ненулевое число  является бесконечно малым тогда и только
тогда, когда
является бесконечно малым тогда и только
тогда, когда 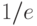 бесконечно велико. В самом деле, пусть,
например,
бесконечно велико. В самом деле, пусть,
например, 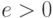 бесконечно мало. Тогда
бесконечно мало. Тогда 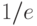 больше
любого стандартного числа
больше
любого стандартного числа  , так как
, так как 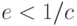 . Остальные
случаи разбираются аналогично.
. Остальные
случаи разбираются аналогично.
Сумма и произведение двух конечных чисел конечны. Если  по модулю меньше стандартного числа
по модулю меньше стандартного числа  , а
, а  —
стандартного числа
—
стандартного числа  , то
, то  по модулю
меньше стандартного числа
по модулю
меньше стандартного числа 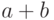 , а
, а 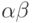 по модулю
меньше
по модулю
меньше  . (Неравенства в гипердействительных числах можно складывать и
умножать, так как обычные свойства неравенств записываются
формулами и допускают перенос.)
. (Неравенства в гипердействительных числах можно складывать и
умножать, так как обычные свойства неравенств записываются
формулами и допускают перенос.)
В обычном курсе математического анализа аналогом этого
рассуждения является утверждение о том, что сумма и произведение
ограниченных последовательностей ограничены. Другое стандартное
утверждение из курса анализа — о произведении ограниченных и
бесконечно малых (сходящихся к нулю) последовательностей — также
имеет естественный аналог: произведение конечного и бесконечно
малого гипердействительных чисел является бесконечно малым
гипердействительным числом. Доказательство также вполне
традиционно: если  не превосходит стандартного
числа
не превосходит стандартного
числа  , а
, а  меньше любого стандартного
положительного числа, то
меньше любого стандартного
положительного числа, то 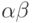 меньше любого стандартного
положительного
меньше любого стандартного
положительного  , так как
, так как  .
.
Два гипердействительных числа 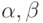 называются
бесконечно близкими, если их разность бесконечно мала.
Обозначение:
называются
бесконечно близкими, если их разность бесконечно мала.
Обозначение:  .
.
172. Докажите, что если  , то
, то  для любого
гипердействительного
для любого
гипердействительного  , а
, а  для любого конечного
гипердействительного
для любого конечного
гипердействительного  . Покажите, что условие конечности
существенно.
. Покажите, что условие конечности
существенно.
173. Покажите, что два конечных гипердействительных числа бесконечно близки тогда и только тогда, когда между ними нельзя вставить двух разных стандартных чисел.
Легко проверить, что отношение бесконечной близости является отношением эквивалентности на множестве гипердействительных чисел. Классы эквивалентности этого отношения иногда называют монадами (термин, использовавшийся еще Лейбницем).
