Ультрафильтры и компактность
Теорема 75. Всякий фильтр  на множестве
на множестве  можно расширить до
ультрафильтра
можно расширить до
ультрафильтра 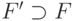 .
.
Доказательство этой теоремы неконструктивно: мы не предъявляем такого фильтра, а устанавливаем его существование с помощью леммы Цорна (см. [6]). Нужно только заметить, что объединение любой цепи фильтров является фильтром (что непосредственно следует из определения).
Другими словами, пока фильтр не станет ультрафильтром, мы берем "промежуточное" множество и расширяем фильтр, объявляя его большим, повторяя этот процесс по трансфинитной индукции.
160. Докажите, что на любом бесконечном множестве есть неглавный ультрафильтр. (Указание: расширим фильтр коконечных множеств до ультрафильтра.)
Можно представлять себе элементы множества  как голосующих
(которые никогда не воздерживаются от голосования). При этом
фильтр на
как голосующих
(которые никогда не воздерживаются от голосования). При этом
фильтр на  определяет регламент: решение принимается, если
множество проголосовавших "за" является большим. Аксиомы
фильтра тогда звучат так: решение, против которого все, принято
быть не может; если каждое из двух решений принимается, то они
принимаются и в совокупности; наконец, принятое решение не может
быть отвергнуто, если некоторые из голосовавших против него
передумали.
определяет регламент: решение принимается, если
множество проголосовавших "за" является большим. Аксиомы
фильтра тогда звучат так: решение, против которого все, принято
быть не может; если каждое из двух решений принимается, то они
принимаются и в совокупности; наконец, принятое решение не может
быть отвергнуто, если некоторые из голосовавших против него
передумали.
Свойство ультрафильтра также имеет ясный смысл: по любому вопросу можно принять решение (одно из двух противоположных мнений набирает большинство). Главные ультрафильтры соответствуют диктатуре (существенно мнение лишь одного голосующего); задача 150 показывает, что для конечного числа голосующих любые другие способы не позволяют принять решения по некоторым вопросам.
Ультрафильтры можно использовать для построения любопытных
примеров. Вот один из них. Рассмотрим игру двух участников, в
которой они по очереди объявляют некоторые натуральные числа "
своими". На первом шаге начинающий игру объявляет своими числа
от нуля до некоторого числа 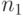 , на втором шаге его противник
присваивает числа от
, на втором шаге его противник
присваивает числа от 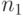 (не включая его) до некоторого
большего числа
(не включая его) до некоторого
большего числа 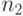 (включая его), затем первый игрок
присваивает числа от
(включая его), затем первый игрок
присваивает числа от 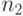 до
до 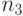 и так далее. Партия
продолжается неограниченно и делит натуральный ряд между первым
и вторым (на два взаимно дополнительных множества). Выигрывает
тот, чье множество большое (принадлежит некоторому фильтру).
и так далее. Партия
продолжается неограниченно и делит натуральный ряд между первым
и вторым (на два взаимно дополнительных множества). Выигрывает
тот, чье множество большое (принадлежит некоторому фильтру).
Если этот фильтр является ультрафильтром, то в этой игре не может быть ничьей. Если ультрафильтр главный, то игра тривиальна — побеждает тот, кто захватит решающее число, и потому первый может гарантировать выигрыш на первом же ходу.
Теорема 76. Если ультрафильтр неглавный, то ни один из игроков не имеет выигрышной стратегии. (Стратегия — это функция, предписывающая следующий ход в зависимости от истории игры. Стратегия считается выигрышной, если ее использование гарантирует выигрыш при любой игре противника.)
Прежде всего отметим, что оба игрока не могут одновременно иметь выигрышные стратегии. (Что будет, если они оба ими воспользуются?) Покажем теперь, что если выигрышную стратегию имеет один, то ее имеет и второй. Совсем просто понять, что если у ходящего вторым есть выигрышная стратегия, то и первый может ей воспользоваться (он должен представить себя вторым, считая, что первый на первом ходу ничего не взял).
Не столь ясно, что выигрышная стратегия первого может быть использована вторым, но и это верно — поскольку конечные множества не влияют на принадлежность ультрафильтру (задача 159), второй может забыть про ход, с которого началась игра, и вообразить себя первым. (Это сделает его первый ход бессмысленным, если этот ход окажется меньше хода противника. В этом случае можно сделать сразу второй ход первого игрока, и далее следовать стратегии.)
161. Проведите это рассуждение подробно.
Сейчас мы докажем теорему компактности с помощью ультрафильтров. Для этого нам понадобится понятие произведения интерпретаций.
Пусть 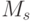 — семейство интерпретаций некоторой (одной и той же)
сигнатуры
— семейство интерпретаций некоторой (одной и той же)
сигнатуры  , индексированное множеством
, индексированное множеством  (для
каждого
(для
каждого 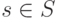 имеется своя интерпретация
имеется своя интерпретация 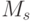 ). Определим
произведение интерпретаций
). Определим
произведение интерпретаций
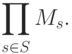
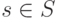 некоторый элемент
интерпретации
некоторый элемент
интерпретации 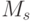 . Иными словами, носитель строимой интерпретации будет декартовым
произведением всех
. Иными словами, носитель строимой интерпретации будет декартовым
произведением всех 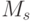 .
.Функциональные символы интерпретировать легко: они применяются
отдельно в каждой компоненте. Именно так определяется
произведение групп или колец в алгебре. Остается определить
предикатные символы. В алгебре два элемента в произведении колец
или групп считаются равными, если все их компоненты равны. По
аналогии будем считать, что два элемента  и
и  делают истинным двуместный предикат
делают истинным двуместный предикат  ,
если
,
если 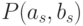 истинно в интерпретации
истинно в интерпретации 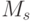 для всех
для всех  . (Мы взяли двуместный символ для примера, то же самое можно сделать и
для символов любой валентности.)
. (Мы взяли двуместный символ для примера, то же самое можно сделать и
для символов любой валентности.)
Для произведения двух упорядоченных множеств (индексное
множество  равно
равно 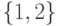 , сигнатура есть
, сигнатура есть 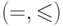 ) возникает покомпонентный порядок на парах:
) возникает покомпонентный порядок на парах: 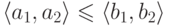 , если
, если  и
и 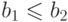 . Заметим, что такой порядок на
произведении двух линейно упорядоченных множеств уже не будет
линейным (если сомножители состоят более чем из одного элемента).
. Заметим, что такой порядок на
произведении двух линейно упорядоченных множеств уже не будет
линейным (если сомножители состоят более чем из одного элемента).
Нам это не нравится: мы хотим, чтобы произведение интерпретаций
обладало бы всеми свойствами, которыми обладают сомножители.
Введем понятие фильтрованного произведения (по модулю данного фильтра).
Пусть на множестве индексов  задан фильтр
задан фильтр  . Изменим определение истинности предикатов и будем считать,
что элементы
. Изменим определение истинности предикатов и будем считать,
что элементы 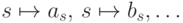 делают
истинным предикат
делают
истинным предикат  , если
, если 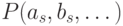 истинно
"для большинства
истинно
"для большинства  ", то есть если множество
", то есть если множество 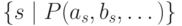 принадлежит фильтру
принадлежит фильтру  . В остальном
(носитель, функциональные символы) определение остается прежним.
. В остальном
(носитель, функциональные символы) определение остается прежним.
Что будет равенством в фильтрованном произведении нормальных
интерпретаций? Два элемента произведения (то есть функции на
множестве индексов) равны, если они "совпадают почти
всюду", то есть множество индексов, где они совпадают,
принадлежит фильтру. При этом полученная интерпретация не будет
нормальной. Чтобы перейти к нормальной, нужно рассмотреть классы
равных элементов — как это делается, скажем, для пространства 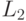 интегрируемых с квадратом функций, где элементами являются
не сами функции, а их классы с точностью до совпадения почти всюду.
интегрируемых с квадратом функций, где элементами являются
не сами функции, а их классы с точностью до совпадения почти всюду.
162. Что можно сказать про фильтрованное произведение по главному фильтру?
Вернемся к нашему примеру: произведению линейно упорядоченных
множеств. Будет ли оно линейно упорядоченным? Это зависит от
фильтра. Например, если фильтр состоит только из множества  ,
то фильтрованное произведение совпадает с определенным ранее, и
линейного порядка не получится. Но если фильтр является
ультрафильтром, то будет. В самом деле, рассмотрим два элемента
,
то фильтрованное произведение совпадает с определенным ранее, и
линейного порядка не получится. Но если фильтр является
ультрафильтром, то будет. В самом деле, рассмотрим два элемента  и
и  в произведении и
два множества
в произведении и
два множества  и
и 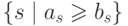 . В объединении они покрывают все
. В объединении они покрывают все  , и потому (если у нас
ультрафильтр) одно из них должно быть большим (если оно не
большое, так малое, его дополнение большое и содержится во
втором множестве).
, и потому (если у нас
ультрафильтр) одно из них должно быть большим (если оно не
большое, так малое, его дополнение большое и содержится во
втором множестве).
163. Докажите, что в фильтрованном произведении нормальных интерпретаций функции и предикаты корректны относительно равенства (то есть совпадения почти всюду): при замене аргументов на равные значение функции совпадает с прежним почти всюду, а значение предиката не меняется.
Это утверждение можно сформулировать так: аксиомы равенства истинны в фильтрованном произведении нормальных интерпретаций. Для ультрафильтров верно и более общее свойство: любая формула, истинная во всех интерпретациях, истинна в фильтрованном произведении по модулю ультрафильтра. Поэтому именно такие ультрапроизведения (фильтрованные по модулю ультрафильтра) представляют основной интерес для логики.
Мы сейчас докажем это свойство по индукции. Как обычно, надо предварительно распространить его на формулы с параметрами.
