Ультрафильтры и компактность
Теорема 77 (Лося об ультрапроизведениях).
Пусть параметрами формулы  являются переменные
являются переменные 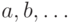 Она будет истинной в ультрапроизведении
Она будет истинной в ультрапроизведении  при значениях параметров
при значениях параметров 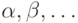 тогда и
только тогда, когда множество тех
тогда и
только тогда, когда множество тех  , при которых
, при которых  истинна в
истинна в 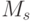 при значениях параметров
при значениях параметров 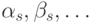 , принадлежит ультрафильтру.
, принадлежит ультрафильтру.
Наглядно утверждение теоремы можно сформулировать так: голосование можно проводить не только по атомарным вопросам, а для любых формул. Для замкнутых формул про параметры можно ничего не говорить, и мы получаем, что формула истинна в ультрапроизведении, если и только если она истинна в большинстве (с точки зрения ультрафильтра) сомножителей. В частности, если формула истинна во всех сомножителях, то она истинна и в ультрапроизведении. Это важное утверждение заслуживает особого упоминания:
Следствие. Ультрапроизведение семейства моделей некоторой теории является моделью той же теории.
Докажем теорему Лося индукцией по построению формулы. Для атомарных формул оно непосредственно следует из определения истинности предикатов.
Пусть формула  является конъюнкцией двух других формул
является конъюнкцией двух других формул 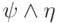 , для которых утверждение уже верно. Тогда
множество тех индексов, для которых
, для которых утверждение уже верно. Тогда
множество тех индексов, для которых  истинно, является
пересечение множеств тех индексов, где истинны
истинно, является
пересечение множеств тех индексов, где истинны  и
и 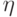 . Тем самым нам нужно такое свойство ультрафильтра: пересечение
двух множеств является большим тогда и только тогда, когда оба
они большие. Оно непосредственно следует из определения фильтра
(здесь неважно, что это ультрафильтр), поскольку пересечение
содержится в обоих множествах.
. Тем самым нам нужно такое свойство ультрафильтра: пересечение
двух множеств является большим тогда и только тогда, когда оба
они большие. Оно непосредственно следует из определения фильтра
(здесь неважно, что это ультрафильтр), поскольку пересечение
содержится в обоих множествах.
Для объединения соответствующее свойство звучит так: объединение 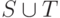 двух множеств большое тогда и только тогда, когда хотя
бы одно из множеств
двух множеств большое тогда и только тогда, когда хотя
бы одно из множеств  и
и  большое. В одну сторону
(если одно из множеств большое, то и объединение таково) это вытекает из
определения фильтра. В обратную сторону надо воспользоваться
свойствами ультрафильтра: если
большое. В одну сторону
(если одно из множеств большое, то и объединение таково) это вытекает из
определения фильтра. В обратную сторону надо воспользоваться
свойствами ультрафильтра: если 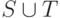 большое, а оба
множества
большое, а оба
множества  и
и  — нет, то они малые, их дополнения
большие, пересечение дополнений большое, и не пересекается с
— нет, то они малые, их дополнения
большие, пересечение дополнений большое, и не пересекается с 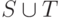 , что невозможно.
, что невозможно.
Пусть формула  имеет вид
имеет вид  . Тогда
имеет место такая цепочка: (
. Тогда
имеет место такая цепочка: (  истинна в
ультрапроизведении
истинна в
ультрапроизведении  ложна в
нем
ложна в
нем  множество индексов тех сомножителей,
где
множество индексов тех сомножителей,
где  истинна, не является большим
истинна, не является большим  это
множество является малым
это
множество является малым  его дополнение
большое
его дополнение
большое  множество номеров тех сомножителей,
где
множество номеров тех сомножителей,
где  ложна (то есть
ложна (то есть  истинна), большое).
истинна), большое).
Импликация сводится к уже рассмотренным случаям ( 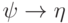 эквивалентна
эквивалентна 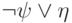 ); можно также сразу заменить
формулу на эквивалентную без импликации.
); можно также сразу заменить
формулу на эквивалентную без импликации.
Наиболее интересен случай кванторов. Можно ограничиться
квантором существования (квантор всеобщности сводится к нему и к
отрицаниям). Он разбирается так (мы используем не вполне
корректные обозначения — надеемся, они не вызовут путаницы).
Пусть формула 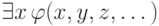 истинна в ультрапроизведении. Это значит, что существует функция
истинна в ультрапроизведении. Это значит, что существует функция  , для которой
, для которой 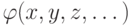 истинно в ультрапроизведении. По предположению индукции это означает,
что для большинства
истинно в ультрапроизведении. По предположению индукции это означает,
что для большинства  формула
формула 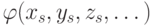 истинна в
истинна в 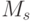 . Но тогда для этих индексов
. Но тогда для этих индексов  и формула
и формула 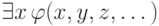 истинна в
истинна в 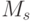 , что и требовалось. Обратное рассуждение
аналогично: если для большинства
, что и требовалось. Обратное рассуждение
аналогично: если для большинства  найдется
соответствующее значение
найдется
соответствующее значение 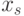 , то эти
, то эти 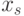 можно
собрать в функцию (доопределив ее как угодно на малом множестве остальных
можно
собрать в функцию (доопределив ее как угодно на малом множестве остальных  ), и
эта функция будет искомым значением
), и
эта функция будет искомым значением  в
ультрапроизведении.
в
ультрапроизведении.
Теорема Лося доказана.
Мы уже говорили, что произведение нормальных интерпретаций может не быть нормальным. Но теорема Лося гарантирует, что в ультрапроизведении нормальных интерпретаций выполнены аксиомы равенства (поскольку они выполнены в каждом сомножителе), и потому равенство является отношением эквивалентности, и классы эквивалентности уже дают нормальную интерпретацию (с теми же истинными формулами).
Теорема Лося позволяет дать прямое доказательство теоремы
компактности (теорема 50). Она утверждает, что
если всякое конечное подмножество данного множества замкнутых
формул  совместно (имеет модель), то и все множество
совместно (имеет модель), то и все множество  совместно.
совместно.
Модель для всего множества  строится как ультрапроизведение.
Индексами будут конечные подмножества множества
строится как ультрапроизведение.
Индексами будут конечные подмножества множества  . Для каждого
из них сомножителем будет существующая по условию модель. Теперь
надо правильно подобрать фильтр на семействе конечных
подмножеств множества
. Для каждого
из них сомножителем будет существующая по условию модель. Теперь
надо правильно подобрать фильтр на семействе конечных
подмножеств множества  . Нам нужно, чтобы для каждого
. Нам нужно, чтобы для каждого 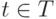 семейство всех конечных подмножеств, содержащих
семейство всех конечных подмножеств, содержащих  , было
бы большим. (В этом случае теорема Лося гарантирует, что
, было
бы большим. (В этом случае теорема Лося гарантирует, что  будет
истинно в ультрапроизведении.)
будет
истинно в ультрапроизведении.)
Как построить такой фильтр? Для каждого конечного 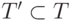 рассмотрим семейство
рассмотрим семейство 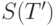 всех конечных подмножеств,
содержащих
всех конечных подмножеств,
содержащих 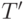 . Очевидно, пересечение таких семейств снова
будет семейством такого вида (
. Очевидно, пересечение таких семейств снова
будет семейством такого вида ( 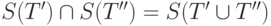 ), так что после добавления всех надмножеств всех таких
множеств получится фильтр. Остается расширить этот фильтр до
ультрафильтра по теореме 75. Теорема компактности доказана.
), так что после добавления всех надмножеств всех таких
множеств получится фильтр. Остается расширить этот фильтр до
ультрафильтра по теореме 75. Теорема компактности доказана.
Поучительно проследить до конца, что дает такого рода построение для какого-нибудь конкретного примера. Вспомним построение нестандартного натурального ряда. Оно использовало теорему компактности. Сочетая его с приведенным только что доказательством теоремы компактности (и кое-что упростив), получаем такую конструкцию.
Рассмотрим натуральные числа как интерпретацию сигнатуры 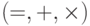 . Рассмотрим ультрапроизведение
. Рассмотрим ультрапроизведение 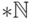 счетного числа таких интерпретаций по модулю какого-либо
неглавного ультрафильтра. Теорема Лося говорит, что в этой
интерпретации будут истинны те же формулы, что в натуральном
ряду, то есть что
счетного числа таких интерпретаций по модулю какого-либо
неглавного ультрафильтра. Теорема Лося говорит, что в этой
интерпретации будут истинны те же формулы, что в натуральном
ряду, то есть что 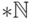 элементарно эквивалентна
стандартной интерпретации
элементарно эквивалентна
стандартной интерпретации 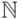 .
.
Покажем, что 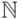 не изоморфна
не изоморфна 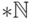 . В
самом деле, при таком изоморфизме нуль обязан переходить в элемент
. В
самом деле, при таком изоморфизме нуль обязан переходить в элемент 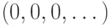 (точнее, в класс этого элемента относительно
равенства), поскольку такой класс обладает свойствами нуля,
однозначно его определяющими (в
(точнее, в класс этого элемента относительно
равенства), поскольку такой класс обладает свойствами нуля,
однозначно его определяющими (в 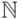 , а потому и
в
, а потому и
в  ). По аналогичным причинам единица переходит в
класс
). По аналогичным причинам единица переходит в
класс 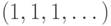 и вообще число
и вообще число  соответствует
классу
соответствует
классу 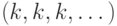 . А класс
. А класс 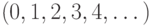 отличается
от любого класса
отличается
от любого класса 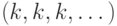 (они совпадают в единственном сомножителе,
а одноэлементное множество является малым, так как ультрафильтр
неглавный). Таким образом, построенная нами модель
(они совпадают в единственном сомножителе,
а одноэлементное множество является малым, так как ультрафильтр
неглавный). Таким образом, построенная нами модель  не является стандартной.
не является стандартной.
Аналогичное рассуждение позволяет построить и нестандартные модели действительных чисел (о которых мы будем говорить в следующем разделе).
