Лексический анализ
Алгоритмы построения конечных автоматов
Построение недетерминированного конечного автомата по регулярному выражению
Рассмотрим алгоритм построения по регулярному выражению недетерминированного конечного автомата, допускающего тот же язык.
Алгоритм 3.1. Построение недетерминированного конечного автомата по регулярному выражению.
Вход. Регулярное выражение r в алфавите T.
Выход. НКА M, такой что L(M) = L(r).
Метод.Автомат для выражения строится композицией из автоматов, соответствующих подвыражениям. На каждом шаге построения строящийся автомат имеет в точности одно заключительное состояние, в начальное состояние нет переходов из других состояний и нет переходов из заключительного состояния в другие.
- Для выражения e строится автомат
- Для выражения
 строится автомат
строится автомат
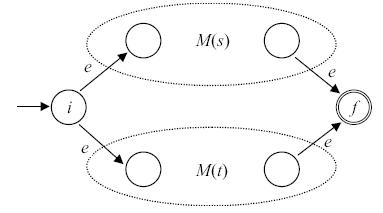
- Пусть M(s) и M(t) - НКА для регулярных выражений s и t соответственно.
- Для выражения s|t автомат M(s|t) строится как показано на рис. 3.7. Здесь i - новое начальное состояние и f - новое заключительное состояние. Заметим, что имеет место переход по e из i в начальные состояния M(s) и M(t) и переход по e из заключительных состояний M(s) и M(t) в f. Начальное и заключительное состояния автоматов M(s) и M(t) не являются таковыми для автомата M(s|t).
- Для выражения st автомат M(st) строится следующим образом: Начальное состояние автомата M(s) становится начальным для нового автомата, а заключительное состояние M(t) становится заключительным для нового автомата. Начальное состояние M(t) и заключительное состояние M(s) сливаются, то есть все переходы из начального состояния M(t) становятся переходами из заключительного состояния M(s). В новом автомате это объединенное состояние не является ни начальным, ни заключительным.
- Для выражения s* автомат M(s*) строится следующим образом: Здесь i - новое начальное состояние, а f - новое заключительное состояние.
Построение детерминированного конечного автомата по недетерминированному
Рассмотрим алгоритм построения по недетерминированному конечному автомату детерминированного конечного автомата, допускающего тот же язык.
Алгоритм 3.2. Построение детерминированного конечного автомата по недетерминированному.
Вход. НКА M = (Q, T, D, q0, F).
Выход. ДКА  .
.
Метод. Каждое состояние результирующего ДКА - это некоторое множество состояний исходного НКА.
В алгоритме будут использоваться следующие функции: 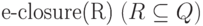 - множество состояний НКА,
достижимых из состояний, входящих в R, посредством только
переходов по e, то есть множество
- множество состояний НКА,
достижимых из состояний, входящих в R, посредством только
переходов по e, то есть множество
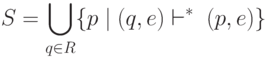
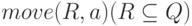 - множество состояний НКА, в
которые есть переход на входе a для состояний из R, то есть
множество
- множество состояний НКА, в
которые есть переход на входе a для состояний из R, то есть
множество
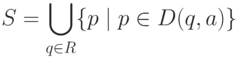
Вначале Q' и D' пусты. Выполнить шаги 1-4:
(1) Определить  .
.
(2) Добавить  в Q' как непомеченное состояние
в Q' как непомеченное состояние
(3) Выполнить следующую процедуру:
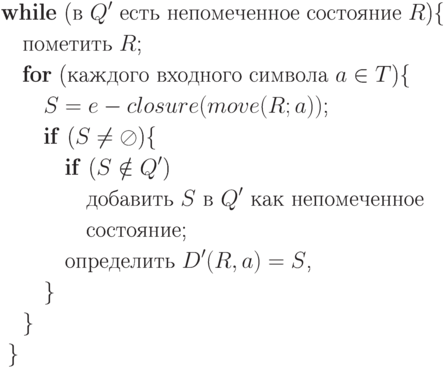
(4) Определить  .
.
Пример 3.6. Результат применения алгоритма 3.2 приведен на рис. 3.10.
Построение детерминированного конечного автомата по регулярному выражению
Приведем теперь алгоритм построения по регулярному выражению детерминированного конечного автомата, допускающего тот же язык [?].
Пусть дано регулярное выражение r в алфавите T. К регулярному выражению r добавим маркер конца: (r)#. Такое регулярное выражение будем называть пополненным. В процессе своей работы алгоритм будет использовать пополненное регулярное выражение.
Алгоритм будет оперировать с синтаксическим деревом
для пополненного регулярного выражения (r)#, каждый
лист которого помечен символом 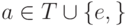 , а каждая
внутренняя вершина помечена знаком одной из операций:
, а каждая
внутренняя вершина помечена знаком одной из операций:  (конкатенация), | (объединение), * (итерация).
(конкатенация), | (объединение), * (итерация).
Каждому листу дерева (кроме e -листьев) присвоим уникальный номер, называемый позицией, и будем использовать его, с одной стороны, для ссылки на лист в дереве, и, с другой стороны, для ссылки на символ, соответствующий этому листу. Заметим, что если некоторый символ используется в регулярном выражении несколько раз, он имеет несколько позиций.
Обойдем дерево T снизу-вверх слева-направо и вычислим четыре функции: nullable,firstpos, lastpos и followpos. Три первые функции - nullable, firstpos и lastpos - определены на узлах дерева, а followpos - на множестве позиций. Значением всех функций, кроме nullable, является множество позиций. Функция followpos вычисляется через три остальные функции.
Функция firstpos(n) для каждого узла n синтаксического дерева регулярного выражения дает множество позиций, которые соответствуют первым символам в подцепочках, генерируемых подвыражением с вершиной в n. Аналогично, lastpos(n) дает множество позиций, которым соответствуют последние символы в подцепочках, генерируемых подвыражениями с вершиной n. Для узла n, поддеревья которого (то есть деревья, у которых узел n является корнем) могут породить пустое слово, определим nullable(n)=true, а для остальных узлов nullable(n)=false.
Таблица для вычисления функций nullable, firstpos и lastpos приведена на рис. 3.11.
Пример 3.7.На рис. 3.12 приведено cинтаксическое дерево для пополненного регулярного выражения (a|b)*abb# с результатом вычисления функций firstpos и lastpos. Слева от каждого узла расположено значение firstpos, справа от узла - значение lastpos. Заметим, что эти функции могут быть вычислены за один обход дерева.
Если i - позиция, то followpos(i) есть множество позиций j таких, что существует некоторая строка ... cd ..., входящая в язык, описываемый регулярным выражением, такая, что позиция i соответствует этому вхождению c, а позиция j - вхождению d.