Лексический анализ
Основная задача лексического анализа - разбить входной текст, состоящий из последовательности одиночных символов, на последовательность слов, или лексем, то есть выделить эти слова из непрерывной последовательности символов. Все символы входной последовательности с этой точки зрения разделяются на символы, принадлежащие каким-либо лексемам, и символы, разделяющие лексемы (разделители). В некоторых случаях между лексемами может и не быть разделителей. С другой стороны, в некоторых языках лексемы могут содержать незначащие символы (например, символ пробела в Фортране). В Си разделительное значение символов-разделителей может блокироваться (" \ " в конце строки внутри " ...").
Обычно все лексемы делятся на классы. Примерами таких классов являются числа (целые, восьмеричные, шестнадцатиричные, действительные и т.д.), идентификаторы, строки. Отдельно выделяются ключевые слова и символы пунктуации (иногда их называют символы-ограничители). Как правило, ключевые слова - это некоторое конечное подмножество идентификаторов. В некоторых языках (например, ПЛ/1) смысл лексемы может зависеть от ее контекста и невозможно провести лексический анализ в отрыве от синтаксического.
Для осуществления двух дальнейших фаз анализа лексический анализатор выдает информацию двух типов: для синтаксического анализатора, работающего вслед за лексическим, существенна информация о последовательности классов лексем, ограничителей и ключевых слов, а для контекстного анализатора, работающего вслед за синтаксическим, существенна информация о конкретных значениях отдельных лексем (идентификаторов, чисел и т.д.).
Таким образом, общая схема работы лексического анализатора такова. Сначала выделяется отдельная лексема (при этом, возможно, используются символы- разделители). Ключевые слова распознаются явным выделением непосредственно из текста, либо сначала выделяется идентификатор, а затем делается проверка на принадлежность его множеству ключевых слов.
Если выделенная лексема является ограничителем, то этот ограничитель (точнее, некоторый его признак) выдается как результат лексического анализа. Если выделенная лексема является ключевым словом, то выдается признак соответствующего ключевого слова. Если выделенная лексема является идентификатором - выдается признак идентификатора, а сам идентификатор сохраняется отдельно. Наконец, если выделенная лексема принадлежит какому-либо из других классов лексем (например, лексема представляет собой число, строку и т.д.), то выдается признак соответствующего класса, а значение лексемы сохраняется отдельно.
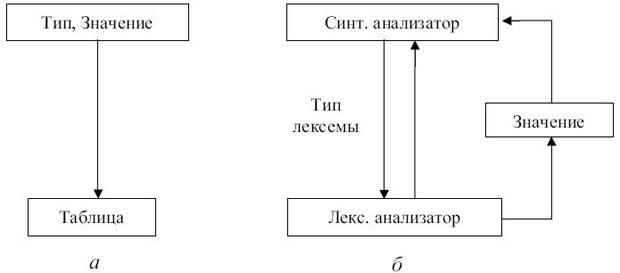
Лексический анализатор может быть как самостоятельной фазой трансляции, так и подпрограммой, работающей по принципу "дай лексему". В первом случае ( рис. 3.1, а) выходом анализатора является файл лексем, во втором - ( рис. 3.1., б) лексема выдается при каждом обращении к анализатору (при этом, как правило, признак класса лексемы возвращается как результат функции "лексический анализатор", а значение лексемы передается через глобальную переменную). С точки зрения обработки значений лексем, анализатор может либо просто выдавать значение каждой лексемы, при этом построение таблиц объектов (идентификаторов, строк, чисел и т.д.) переносится на более поздние фазы, либо он может самостоятельно строить таблицы объектов. В этом случае в качестве значения лексемы выдается указатель на вход в соответствующую таблицу.
Работа лексического анализатора задается некоторым конечным автоматом. Однако, непосредственное описание конечного автомата неудобно с практической точки зрения. Поэтому для задания лексического анализатора, как правило, используется либо регулярное выражение, либо праволинейная грамматика. Все три формализма (конечных автоматов, регулярных выражений и праволинейных грамматик) имеют одинаковую выразительную мощность. В частности, по регулярному выражению или праволинейной грамматике можно сконструировать конечный автомат, распознающий тот же язык.
Регулярные множества и выражения
Введем понятие регулярного множества, играющего важную роль в теории формальных языков.
Регулярное множество в алфавите T определяется рекурсивно следующим образом:
-
 (пустое множество) - регулярное множество в
алфавите T ;
(пустое множество) - регулярное множество в
алфавите T ; - {e} - регулярное множество в алфавите T ( e - пустая цепочка);
-
{a} - регулярное множество в алфавите T для каждого
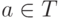 ;
; - если P и Q - регулярные множества в алфавите T, то
регулярными являются и множества
-
 ,
, 
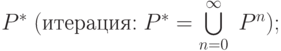
-
- ничто другое не является регулярным множеством в алфавите T.
Итак, множество в алфавите T регулярно тогда и только
тогда, когда оно либо 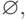 либо {e}, либо {a} для некоторого
либо {e}, либо {a} для некоторого 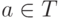 , либо его можно получить из этих множеств применением
конечного числа операций объединения, конкатенации и
итерации.
, либо его можно получить из этих множеств применением
конечного числа операций объединения, конкатенации и
итерации.
Приведенное выше определение регулярного множества позволяет ввести следующую удобную форму его записи, называемую регулярным выражением.
Регулярное выражение в алфавите T и обозначаемое им регулярное множество в алфавите T определяются рекурсивно следующим образом:
-
 регулярное выражение, обозначающее регулярное
множество
регулярное выражение, обозначающее регулярное
множество  ;
; - {e} - регулярное выражение, обозначающее регулярное множество {e} ;
- {a} - регулярное выражение, обозначающее регулярное множество {a} ;
- если p и q - регулярные выражения, обозначающие регулярные множества P и Q соответственно, то
- ничто другое не является регулярным выражением в алфавите T.
Мы будем опускать лишние скобки в регулярных выражениях, договорившись о том, что операция итерации имеет наивысший приоритет, затем идет операции конкатенации, наконец, операция объединения имеет наименьший приоритет.
Кроме того, мы будем пользоваться записью p+ для обозначения pp*. Таким образом, запись (a|((ba)(a*))) эквивалентна a|ba+.
Также, мы будем использовать запись L(r) для регулярного множества, обозначаемого регулярным выражением r.
Пример 3.1. Несколько примеров регулярных выражений и обозначаемых ими регулярных множеств:
- a(e|a)|b - обозначает множество {a; b; aa} ;
- a(a|b)* - обозначает множество всевозможных цепочек, состоящих из a и b, начинающихся с a ;
- (a|b)*(a|b)(a|b)* - обозначает множество всех непустых цепочек, состоящих из a и b, то есть множество {a, b}+ ;
- ((0|1)(0|1)(0|1))* - обозначает множество всех цепочек, состоящих из нулей и единиц, длины которых делятся на 3.
Ясно, что для каждого регулярного множества можно найти регулярное выражение, обозначающее это множество, и наоборот. Более того, для каждого регулярного множества существует бесконечно много обозначающих его регулярных выражений.
Будем говорить, что регулярные выражения равны или эквивалентны ( = ), если они обозначают одно и то же регулярное множество.
Существуют алгебраические законы, позволяющие осуществлять эквивалентное преобразование регулярных выражений.
Лемма. Пусть p, q и r - регулярные выражения. Тогда справедливы следующие соотношения:
- p|q = q|p ;
-
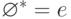 ;
; - p|(q|r) = (p|q)|r ;
- p(qr) = (pq)r ;
- p(q|r) = pq|pr ;
- (p|q)r = pr|qr ;
- pe = ep = p ;
-
 ;
; - p* = p|p* ;
- (p*)* = p* ;
- p|p = p ;
-
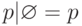 ;
;
Следствие. Для любого регулярного выражения
существует эквивалентное регулярное выражение,
которое либо есть  , либо не содержит в своей записи
, либо не содержит в своей записи 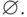
В дальнейшем будем рассматривать только регулярные
выражения, не содержащие в своей записи 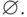 При практическом описании лексических структур бывает
полезно сопоставлять регулярным выражениям некоторые
имена, и ссылаться на них по этим именам. Для определения
таких имен мы будем использовать запись вида
При практическом описании лексических структур бывает
полезно сопоставлять регулярным выражениям некоторые
имена, и ссылаться на них по этим именам. Для определения
таких имен мы будем использовать запись вида
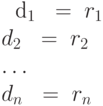
где di - различные имена, а каждое ri - регулярное
выражение над символами  , то есть
символами основного алфавита и ранее определенными
символами (именами). Таким образом, для любого ri
можно построить регулярное выражение над T, повторно
заменяя имена регулярных выражений на обозначаемые ими
регулярные выражения.
, то есть
символами основного алфавита и ранее определенными
символами (именами). Таким образом, для любого ri
можно построить регулярное выражение над T, повторно
заменяя имена регулярных выражений на обозначаемые ими
регулярные выражения.
Пример 3.2. Несколько примеров использования имен для обозначения регулярных выражений.
- Регулярное выражение для множества идентификаторов.
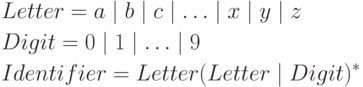
- Регулярное выражение для множества чисел в десятичной
записи.
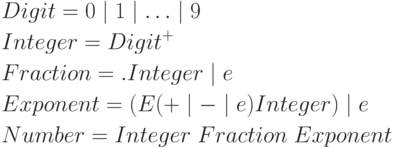

 ,
,