Семантика контекстно-свободных языков
Введение
Допустим, что нам нужно дать точное определение двоичной системы записи чисел. Это можно сделать многими способами. В данном разделе мы рассмотрим метод, который может быть использован и для других систем счисления. В случае двоичной системы этот метод сводится к определению, основанному на следующей констекстно-свободной (КС) грамматике.
B -> 0 B -> 1 L -> B L -> LB N -> L N -> L.LПример 1.1.
Здесь терминальными символами являются ".", "0" и "1", нетерминальными - B, L и N, обозначающие соответственно бит, список битов и число. Двоичным числом будем считать любую цепочку терминальных символов, выводимую из N при помощи правил ( пример 1.1). Эта грамматика в действительности выражает тот факт, что двоичное число представляет собой последовательность из одного или более нулей и единиц, за которой может следовать точка и еще одна последовательность нулей и единиц. Кроме того, грамматика приписывает каждому двоичному числу определенную древовидную структуру. Например, цепочка 1101.01 получает следующую структуру:
Естественно определять значение двоичной записи ( пример 1.1) с помощью некоторого пошагового процесса, сопоставленного ее структуре ( рис. 1.2); значение всей двоичной записи строится из значений отдельных частей. Это можно сделать, приписав каждому нетерминалу атрибуты следующим образом:
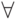 бит B имеет целочисленный атрибут "значение",
обозначаемый v(B).
бит B имеет целочисленный атрибут "значение",
обозначаемый v(B).
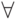 список битов L имеет целочисленный атрибут "длина",
обозначаемый l(L).
список битов L имеет целочисленный атрибут "длина",
обозначаемый l(L). 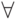 список битов L имеет целочисленный
атрибут "значение", обозначаемый v(L).
список битов L имеет целочисленный
атрибут "значение", обозначаемый v(L).
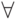 число N имеет атрибут "значение", являющийся
рациональным числом и обозначаемый v(N).
число N имеет атрибут "значение", являющийся
рациональным числом и обозначаемый v(N).
(Заметим, что у всех нетерминалов L по два атрибута; вообще говоря, каждому нетерминалу можно приписывать любое желаемое число атрибутов).
Грамматику ( пример 1.1) можно теперь расширить так, чтобы каждому синтаксическому правилу отвечали семантические правила.
B -> 0 v(B) = 0 B -> 1 v(B) = 1 L -> B v(L) = v(B); l(L) = 1 L1 -> L2B v(L1) = 2v(L2) + v(B); l(L1) = l(L2) + 1 N -> L v(N) = v(L) N -> L1:L2 v(N) = v(L1) + v(L2)=2l(L2)Пример 1.3.
(Индексы в четвертом и шестом правилах применяются для того, чтобы различать вхождения одноименных нетерминалов.). В этих семантических правилах значения атрибутов всех нетерминалов определяются через значения атрибутов их непосредственных потомков, так что окончательные значения определены для всех атрибутов. Предполагается, что смысл обозначений, использованных для записи семантических правил, понятен. Отметим, например, что символ "0" в семантическом правиле v(B) = 0 понимается не так, как символ "0" в синтаксическом правиле B -> 0. B первом случае "0" обозначает математическое понятие, а именно число нуль, во втором - некоторый символ, имеющий эллиптическую форму. B каком-то смысле, то, что эти два символа выглядят одинаково, - не более чем простое совпадение.
Структуру ( рис. 1.2) можно расширить, выписав явно атрибуты при всех узлах.
Таким образом, " 1101.01 " обозначает 13.25 (в десятичной записи).
Такой способ определения семантики КС-языков в сущности хорошо известен, так как он уже использовался несколькими авторами. Однако существует важное расширение этого метода. Именно это расширение и представляет для нас интерес.
Предположим, например, что мы хотим определить семантику двоичной записи другим способом, более близким к нашему обычному ее пониманию. Первая единица в записи 1101.01 на самом деле означает 8, хотя в соответствии с ( рис. 1.4) ей приписывается значение 1. Возможно, поэтому будет лучше определять семантику таким образом, чтобы местоположение символа тоже играло определенную роль. Можно ввести следующие атрибуты:
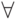 символ B имеет атрибут "значение", являющийся
рациональным числом и обозначаемый v(B).
символ B имеет атрибут "значение", являющийся
рациональным числом и обозначаемый v(B).
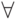 символ B имеет целочисленный атрибут "масштаб ",
обозначаемый s(B).
символ B имеет целочисленный атрибут "масштаб ",
обозначаемый s(B).
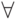 символ L имеет атрибут "значение", являющийся рациональным числом и обозначаемый v(L).
символ L имеет атрибут "значение", являющийся рациональным числом и обозначаемый v(L).
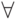 символ L имеет целочисленный атрибут "длина", обозначаемый l(L).
символ L имеет целочисленный атрибут "длина", обозначаемый l(L).
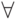 символ L имеет целочисленный атрибут "масштаб", обозначаемый s(L).
символ L имеет целочисленный атрибут "масштаб", обозначаемый s(L).
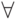 символ N имеет атрибут "значение", принимающий в качестве значений рациональные числа и обозначаемый v(N).
символ N имеет атрибут "значение", принимающий в качестве значений рациональные числа и обозначаемый v(N).
Эти атрибуты можно определить следующим образом:
| Синтаксические правила | Семантические правила |
| B -> 0 | v(B) = 0 |
| B -> 1 | v(B) = 2s(B) |
| L -> B | v(L) = v(B), s(B) = s(L), l(L) = 1 |
| L1 -> L2B | v(L1) = v(L2) + v(B), s(B) = s(L1), s(L2) = s(L1) + 1, l(L1) = l(L2) + 1 |
| N -> L | v(N) = v(L); s(L) = 0 |
| N -> L1.L2 | v(N) = v(L1) + v(L2), s(L1) = 0, s(L2) = -l(L2) |
Здесь при записи семантических правил принято следующее соглашение. Правая часть каждого правила представляет собой определение левой части, таким образом, s(B) = s(L) означает, что сначала должно быть вычислено s(L), а затем полученное значение следует присвоить s(B).
Важным свойством грамматики ( таблица 1.1) является то, что некоторые из атрибутов, которым присваиваются значения, приписаны нетерминалам, стоящим в правой части соответствующего синтаксического правила, в то время как в 1.3 атрибуты левых частей семантических правил относились только к нетерминалам, стоящим в левой части синтаксического правила. Здесь мы используем как синтезированные атрибуты (вычисляемые через атрибуты потомков данного нетерминала), так и унаследованные атрибуты (вычисляемые через атрибуты предков). Синтезированные атрибуты вычисляются в древовидной структуре снизу вверх, а унаследованные - сверху вниз. Грамматика ( таблица 1.1) включает синтезированные атрибуты v(B), v(L), l(L), v(N) и унаследованные атрибуты s(B) и s(L), так что при их вычислении необходимо проходить по дереву в обоих направлениях. Вычисление на структуре, соответствующей цепочке 1101.01, имеет вид:
Можно заметить, что атрибуты "длина" символов L, стоящих справа от точки, должны быть вычислены снизу вверх до того, как будут вычислены (сверху вниз) атрибуты "масштаб" и атрибуты "значение" (снизу вверх).
Грамматика ( таблица 1.1), вероятно, не является "наилучшей возможной" грамматикой для системы двоичной записи, но похоже, что она лучше согласуется с нашей интуицией, чем грамматика ( пример 1.3). (Грамматика, которая более точно соответствует нашему традиционному толкованию двоичной нотации, содержит другое множество правил вывода. Эти правила сопоставляют цепочке битов справа от точки иную структуру, вследствие чего атрибут "длина", не играющий принципиальной роли, становится ненужным.)
Наш интерес к грамматике ( таблица 1.1) вызван не тем, что она представляет собой идеальное определение двоичной системы записи, а тем, что она демонстрирует взаимодействие унаследованных и синтезированных атрибутов. Тот факт, что семантические правила, подобные правилам в ( таблица 1.1), не приводят к зацикленности определения атрибутов, не является очевидным, поскольку здесь атрибуты вычисляются не при однократном обходе дерева в одном направлении. Алгоритм, проверяющий семантические правила на зацикленность, будет описан ниже.
Важность унаследованных атрибутов состоит в том, что они естественно возникают в практике и в очевидном смысле "двойственны" синтезированным атрибутам. Хотя для определения смысла двоичной записи достаточно только синтезированных атрибутов, существует ряд языков, для которых такое ограничение приводит к неуклюжему и неестественному определению семантики. Ситуации, когда встречаются и унаследованные, и синтезированные атрибуты, представляют собой те самые случаи, которые в предшествующих определениях семантики вызывали серьезные трудности.



