Семантика контекстно-свободных языков
Формальные свойства
Придадим теперь идее использования синтезированных и унаследованных атрибутов более точную и более общую форму.
Пусть имеется КС-грамматика G = (V, N, S, P), где V - (конечный) алфавит терминальных и нетерминальных
символов;  - множество нетерминальных символов;
- множество нетерминальных символов;  - "начальный "символ, не входящий в правые части
правил, и P - множество правил.
- "начальный "символ, не входящий в правые части
правил, и P - множество правил.
Семантические правила дополняют G следующим
образом. С каждым символом  связывается конечное
множество атрибутов A(X). A(X) разбивается на два
непересекающихся множества: множество синтезированных
атрибутов A0(X) и множество унаследованных атрибутов A1(X). Множество A1(S) должно быть пустым (то есть
начальный символ S не должен иметь унаследованных
атрибутов); аналогично, множество A0(X) пусто, если X -
терминальный символ. Каждый атрибут R из множества A(X) имеет (возможно, бесконечное) множество значений VR.
Для каждого вхождения X в дерево вывода семантические
правила позволяют определить одно значение из множества VR для соответствующего атрибута.
связывается конечное
множество атрибутов A(X). A(X) разбивается на два
непересекающихся множества: множество синтезированных
атрибутов A0(X) и множество унаследованных атрибутов A1(X). Множество A1(S) должно быть пустым (то есть
начальный символ S не должен иметь унаследованных
атрибутов); аналогично, множество A0(X) пусто, если X -
терминальный символ. Каждый атрибут R из множества A(X) имеет (возможно, бесконечное) множество значений VR.
Для каждого вхождения X в дерево вывода семантические
правила позволяют определить одно значение из множества VR для соответствующего атрибута.
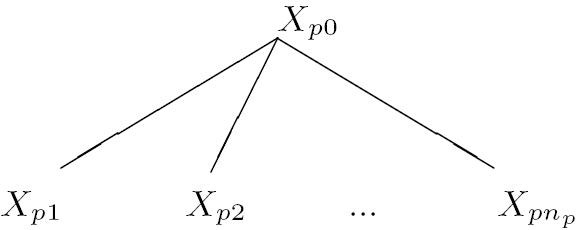
Пусть P состоит из m правил, и пусть p -е правило имеет вид
Xp0 -> Xp1Xp2...Xpnp ;Пример 2.1.
где 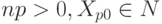 и
и  для 1 <= j <= np.
Семантическими правилами называются функции fpjR,
определ_нные для всех 1 <= p <= m, 0 <= j <= np и
некоторых
для 1 <= j <= np.
Семантическими правилами называются функции fpjR,
определ_нные для всех 1 <= p <= m, 0 <= j <= np и
некоторых 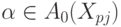 , если j = 0, или
, если j = 0, или  ,
если j > 0. Каждая такая функция представляет собой
отображение из
,
если j > 0. Каждая такая функция представляет собой
отображение из 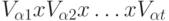 в VR для некоторого
в VR для некоторого  , где все
, где все  являются атрибутами некоторых Xpki, при
являются атрибутами некоторых Xpki, при 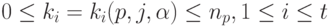 . Другими словами, каждое семантическое правило отображает
значения некоторых атрибутов символов
. Другими словами, каждое семантическое правило отображает
значения некоторых атрибутов символов 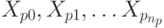 и значение некоторого атрибута символа
и значение некоторого атрибута символа 
Грамматика ( таблица 1.1), например, представляется в виде G = ({0, 1, ".", B, L, N}, {B, L, N}, N, {B -> 0, B -> 1, L -> B, L -> LB, N -> L, N -> L.L}).
Атрибутами здесь являются

для  . Множествами значений атрибутов будут Vv ={рациональные числа}, Vs = Vl = {целые числа}. Типичным
примером правил вывода служит четвeртое правило X40 -> X41X42 , где n4 = 2, X40 = X41 = L, X42 = B. Так же типично и семантическое правило f40v, соответствующее
этому правилу вывода. Оно определяет v(X40) через другие
атрибуты; в данном случае f40v отображает Vv x Vv в Vv согласно формуле f40v(x, y) = x + y. (Это есть не что
иное, как правило v(L1) = v(L2) + v(B) из (
таблица
1.1); используя довольно громоздкую запись, введeнную в предыдущем
абзаце, получим:
. Множествами значений атрибутов будут Vv ={рациональные числа}, Vs = Vl = {целые числа}. Типичным
примером правил вывода служит четвeртое правило X40 -> X41X42 , где n4 = 2, X40 = X41 = L, X42 = B. Так же типично и семантическое правило f40v, соответствующее
этому правилу вывода. Оно определяет v(X40) через другие
атрибуты; в данном случае f40v отображает Vv x Vv в Vv согласно формуле f40v(x, y) = x + y. (Это есть не что
иное, как правило v(L1) = v(L2) + v(B) из (
таблица
1.1); используя довольно громоздкую запись, введeнную в предыдущем
абзаце, получим:
 .
.
Семантические правила используются для сопоставления цепочкам КС языка"значения" следующим образом1На самом деле значение здесь приписывается дереву вывода цепочки, а не ей самой. Если грамматика неоднозначна, это не одно и то же (см. последнюю страницу статьи). - Прим. перев. . Для любого вывода терминальной цепочки t из S при помощи синтаксических правил построим обычное дерево вывода. А именно, корнем дерева будет S, а каждый узел помечается либо терминальным символом, либо нетерминалом Xp0, соответствующим применению p -го правила для некоторого p ; в последнем случае у этого узла будет np непосредственных потомков.
Пусть теперь X - метка некоторого узла дерева и пусть 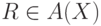 - атрибут символа X. Если
- атрибут символа X. Если  для некоторого p, если же
для некоторого p, если же  для
некоторых j и p. В обоих случаях дерево "в районе" этого узла
имеет вид (
рис.
2.2). По определению атрибут
для
некоторых j и p. В обоих случаях дерево "в районе" этого узла
имеет вид (
рис.
2.2). По определению атрибут  имеет в этом узле значение v, если в соответствующем семантическом правиле
имеет в этом узле значение v, если в соответствующем семантическом правиле

все атрибуты 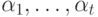 уже определены и имеют в узлах с
метками Xpk1 , ... , Xpkt значения v1, ... , vt соответственно,
а
уже определены и имеют в узлах с
метками Xpk1 , ... , Xpkt значения v1, ... , vt соответственно,
а 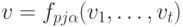 . Процесс вычисления атрибутов на дереве продолжается до тех пор, пока нельзя будет вычислить
больше ни одного атрибута. Вычисленные в результате
атрибуты корня дерева представляют собой "значение",
соответствующее данному дереву вывода (
рис.
1.6).
. Процесс вычисления атрибутов на дереве продолжается до тех пор, пока нельзя будет вычислить
больше ни одного атрибута. Вычисленные в результате
атрибуты корня дерева представляют собой "значение",
соответствующее данному дереву вывода (
рис.
1.6).
Естественно потребовать, чтобы семантические правила давали возможность вычислить все атрибуты произвольного узла в любом дереве вывода. Если это условие выполняется, будем говорить, что семантические правила заданы корректно2В оригинале well defined. - Прим. ред. . Поскольку деревьев вывода, вообще говоря, бесконечно много, важно уметь определять по самой грамматике, являются ли корректными еe семантические правила.
Отметим, что этот метод определения семантики обладает
такой же мощностью, как и всякий другой возможный
метод, в том смысле, что значение любого атрибута в
любом узле может произвольным образом зависеть от
структуры всего дерева. Предположим, например, что в
КС грамматике всем символам, кроме S, приписано по два
унаследованных атрибута: l ("положение") и t ("дерево"), а всем нетерминалам, кроме того, по одному синтезированному
атрибуту s ("поддерево"). Значениями l будут конечные
последовательности положительных целых чисел  , определяющие местонахождение узла в дереве в
соответствии с системой обозначения Дьюи. Атрибуты t и s представляют собой множество упорядоченных пар (l, X), где l - положение узла, а X - символ грамматики, обозначающий метку узла с положением l. Семантическими правилами для каждого синтаксического
правила (
пример
2.1) служат
, определяющие местонахождение узла в дереве в
соответствии с системой обозначения Дьюи. Атрибуты t и s представляют собой множество упорядоченных пар (l, X), где l - положение узла, а X - символ грамматики, обозначающий метку узла с положением l. Семантическими правилами для каждого синтаксического
правила (
пример
2.1) служат
 |
( 2.4) |
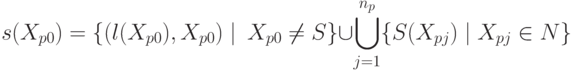
Следовательно, для дерева ( рис. 1.2), например, мы имеем
s(N) = {(1, L), (2, *), (3, L),
(1.1, L), (1.2, B), (3.1, L), (3.2, B),
(1.1.1, L), (1.1.2, B), (1.2.1, 1), (3.1.1, B), (3.2.1, 1),
(1.1.1.1, L), (1.1.1.2, B), (1.1.2.1, 0), (3.1.1.1, 0),
(1.1.1.1.1, B), (1.1.1.2.1, 1), (1.1.1.1.2.1, 1)}.Ясно, что эта запись содержит всю информацию о дереве вывода. Согласно семантическим правилам (2.4), атрибут t во всех узлах (кроме корня) представляет собой множество, характеризующее всe дерево вывода; атрибут l определяет местонахождение этих узлов. Отсюда сразу следует, что любая мыслимая функция, определ_нная на дереве вывода, может быть представлена как атрибут произвольного узла, поскольку эта функция имеет вид f(t, l), для некоторого f. Аналогично, можно показать, что для определения значения, связанного с произвольным деревом вывода, достаточно только синтезированных атрибутов, поскольку синтезированный атрибут w, вычисляемый по формуле
 |
( 2.5) |
в корне дерева полностью определяет всe дерево3В правой части формулы нужно добавить ещe член 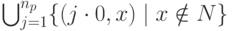 . - Прим. ред.
. Каждое
семантическое правило, определяемое методами этого
раздела, можно рассматривать как функцию этого атрибута w. Следовательно, описанный общий метод по существу
не более мощен, чем метод, вовсе не использующий
наследованных атрибутов. Правда, это утверждение
не следует понимать как практическую рекомендацию,
поскольку семантические правила, не использующие
унаследованных атрибутов, будут зачастую гораздо более
сложными (а также менее понимаемыми и практичными),
чем правила, включающие атрибуты обоих типов. Если
допустить, чтобы атрибуты в каждом узле дерева могли
зависеть от всего дерева, то семантические правила часто
могут стать проще и будут лучше соответствовать нашему
пониманию процесса вычисления.
. - Прим. ред.
. Каждое
семантическое правило, определяемое методами этого
раздела, можно рассматривать как функцию этого атрибута w. Следовательно, описанный общий метод по существу
не более мощен, чем метод, вовсе не использующий
наследованных атрибутов. Правда, это утверждение
не следует понимать как практическую рекомендацию,
поскольку семантические правила, не использующие
унаследованных атрибутов, будут зачастую гораздо более
сложными (а также менее понимаемыми и практичными),
чем правила, включающие атрибуты обоих типов. Если
допустить, чтобы атрибуты в каждом узле дерева могли
зависеть от всего дерева, то семантические правила часто
могут стать проще и будут лучше соответствовать нашему
пониманию процесса вычисления.