Атрибутные грамматики
Введение
Среди всех формальных методов описания языков программирования атрибутные грамматики получили, по- видимому, наибольшую известность и распространение. Причиной этого является то, что формализм атрибутных грамматик основывается на дереве разбора программы в КС-грамматике, что сближает его с хорошо разработанной теорией и практикой построения трансляторов. Вместе с тем выяснилось, что реализация вычислителей для атрибутных грамматик общего вида сталкивается с большими трудностями. В связи с этим было сделано множество попыток рассматривать те или иные классы атрибутных грамматик, обладающими "хорошими" свойствами. К числу таких свойств относятся, прежде всего, простота алгоритма проверки атрибутной грамматики на зацикленность и простота алгоритма вычисления атрибутов для атрибутных грамматик данного класса. В предлагаемой статье дается обзор работ, посвященных этим вопросам.
Определение атрибутных грамматик
Пусть G - КС-грамматика: G = (T, N, P, Z), где T, N, P, Z, соответственно, множество терминальных символов, нетерминальных символов, множество правил вывода и аксиома грамматики. Правила вывода КС- грамматики будем записывать в виде
p : X0->X1 ... Xn (p)
и будем предполагать, что G - редуцированная КС-
грамматика, то есть в ней нет нетерминальных символов,
для которых не существует полного дерева вывода, в которое
входит этот нетерминал. С каждым символом 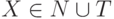 свяжем множество A(X) атрибутов символа X. Некоторые
из множеств A(x) могут быть пусты. Запись a(X) означает,
что
свяжем множество A(X) атрибутов символа X. Некоторые
из множеств A(x) могут быть пусты. Запись a(X) означает,
что 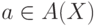 .
.
С каждым правилом вывода 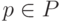 свяжем множество F
семантических правил, имеющих следующую форму:
свяжем множество F
семантических правил, имеющих следующую форму:
a0(i0) = fpa0(i0)(a1(i1), ... , aj(ij));
где ![i_{k}\in [0, n_{p}]](/sites/default/files/tex_cache/d0c1410c81f005116342a86e02655091.png) - номер символа правила p, а ak(ik) - атрибут
символа Xik, то есть
- номер символа правила p, а ak(ik) - атрибут
символа Xik, то есть 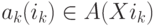 .
В таком случае будем говорить, что a0<i0> "зависит"
от a1(i1), ... , aj(ij) или что a0(i0) "вычисляется по " a1(i1), ... , aj(ij). В частном случае j может быть равно нулю,
тогда будем говорить, что атрибут a0(i0) "получает в качестве
значения константу"
.
В таком случае будем говорить, что a0<i0> "зависит"
от a1(i1), ... , aj(ij) или что a0(i0) "вычисляется по " a1(i1), ... , aj(ij). В частном случае j может быть равно нулю,
тогда будем говорить, что атрибут a0(i0) "получает в качестве
значения константу"
КС-грамматику, каждому символу которой сопоставлено множество атрибутов, а каждому правилу вывода - множество семантических правил, будем называть атрибутной грамматикой ( AG ).
Назовем атрибут a(X0) синтезируемым, если одному
из правил вывода p : X0->X1 ... Xnp сопоставлено
семантическое правило a(0) = fa(0)(...). Назовем атрибут a(Xi) наследуемым, если одному из правил вывода p :
X0->X1 ... Xnp сопоставлено семантическое правило ![a(i) = fa(i)(\dots ), I\in [1, n_{p}]](/sites/default/files/tex_cache/5064dbb4cf57002d9b8d8856a86bcefe.png) . Множество синтезируемых атрибутов
символа X обозначим через S(X), наследуемых атрибутов -
через I(X).
. Множество синтезируемых атрибутов
символа X обозначим через S(X), наследуемых атрибутов -
через I(X).
Пусть правилу вывода p : X0->X1 ... Xnp приписано
семантическое правило a0(i0) = fpa0(i0)(a1(i1), ... , aj(ij)).
Без снижения общности будем считать, что ![a_{k}(i_{k})\in I(X_{0}) \cup np_{n} = 1S(X_{n}), k\in [1, j]](/sites/default/files/tex_cache/ad432ce6a0e69db6d17148412b73ee0b.png) то есть атрибут может
зависеть только от наследуемых атрибутов символа левой
части и синтезируемых атрибутов символов правой части
(условие Бошмана). Кроме того, будем считать, что значение
атрибутов терминальных символов - константы, то есть их
значения определены, но для них нет семантических правил,
определеяющих их значения.
то есть атрибут может
зависеть только от наследуемых атрибутов символа левой
части и синтезируемых атрибутов символов правой части
(условие Бошмана). Кроме того, будем считать, что значение
атрибутов терминальных символов - константы, то есть их
значения определены, но для них нет семантических правил,
определеяющих их значения.
Атрибутированное дерево разбора
Если дана атрибутная грамматика AG и цепочка, принадлежащая языку, определяемому G, то можно построить дерево разбора этой цепочки в грамматике G. В этом дереве каждая вершина помечена символом грамматики G. Припишем теперь каждой вершине множество атрибутов, сопоставленных символу, которым помечена эта вершина. Атрибуты, сопоставленные вхождениям символов в дерево разбора, будем называть вхождениями атрибутов в дерево разбора, а дерево с сопоставленными каждой вершине атрибутами - атрибутированным деревом разбора.
Между вхождениями атрибутов в дерево разбора существуют зависимости, определяемые семантическими правилами, соответствующими примененным синтаксическим правилам.
Для каждого синтаксического правила 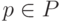 определим D(p) - граф зависимостей атрибутов символов, входящих в
правило p, как ориентированный граф, вершинами которого
служат атрибуты символов, входящих в правило p, и в
котором идет дуга из вершины b(i) в вершину a(j) тогда и
только тогда, когда синтаксическому правилу p сопоставлено
семантическое правило
определим D(p) - граф зависимостей атрибутов символов, входящих в
правило p, как ориентированный граф, вершинами которого
служат атрибуты символов, входящих в правило p, и в
котором идет дуга из вершины b(i) в вершину a(j) тогда и
только тогда, когда синтаксическому правилу p сопоставлено
семантическое правило
![a(j) = fpa(j)(\dots , b(i), \dots ), i, j\in [0, n]](/sites/default/files/tex_cache/de4f995c1efe6d60d0f085fcb6fd091e.png) :
:
Граф зависимостей D(t) дерева разбора t цепочки, принадлежащей языку грамматики G, определим как ориентированный граф, полученный объединением графов зависимостей всех примененных в t синтаксических правил.
Незацикленные атрибутные грамматики
Атрибутная грамматика называется незацикленной, если графы зависимостей деревьев всех цепочек, принадлежащих языку, определяемому грамматикой G, не содержат циклов, и зацикленной, если существует хотя бы одна цепочка, принадлежащая языку, для дерева разбора которой граф D(t) содержит ориентированный цикл.
Теорема B.1. Задача определения того, является ли данная атрибутная грамматика зацикленной, имеет экспоненциальную временную сложность, то есть существует константа c > 0 такая, что любой алгоритм, проверяющий на зацикленность произвольную атрибутную грамматику размера n, должен работать более, чем 2cn/log n шагов на бесконечно большом числе грамматик [1, 2].
Кнутом [3] был предложен алгоритм проверки атрибутных грамматик на зацикленность.
Пусть D(p) - граф зависимостей атрибутов правила
вывода p, а Gi - произвольный ориентированный граф,
вершинами которого служат атрибуты символа Xi правой
части правила вывода p. Обозначим ![D_p[G_1, \ldots , G_{n_p} ]](/sites/default/files/tex_cache/74a305efc9a33cfd6a4f93f3cba45235.png) ориентированный граф, полученный из D(p) добавлением
дуг, идущих из b(i) в a(i), если в графе Gi есть дуга из b в a. Через
ориентированный граф, полученный из D(p) добавлением
дуг, идущих из b(i) в a(i), если в графе Gi есть дуга из b в a. Через  обозначим множество ориентированных графов с
вершинами - атрибутами символа X, через
обозначим множество ориентированных графов с
вершинами - атрибутами символа X, через ![D_p[G_1, \ldots , G_{n_p} ]](/sites/default/files/tex_cache/74a305efc9a33cfd6a4f93f3cba45235.png) - ориентированный граф, вершинами которого служат
атрибуты символа X в правиле вывода p : X0->X1 ... Xnp
и в котором идет дуга из вершины b в вершину a тогда и
только тогда, когда в
- ориентированный граф, вершинами которого служат
атрибуты символа X в правиле вывода p : X0->X1 ... Xnp
и в котором идет дуга из вершины b в вершину a тогда и
только тогда, когда в ![D_p[G_1, \ldots , G_{n_p} ]](/sites/default/files/tex_cache/74a305efc9a33cfd6a4f93f3cba45235.png) есть путь из b(0) в a(0).
есть путь из b(0) в a(0).
Алгоритм B.1. (Алгоритм Кнута). Проверка атрибутной грамматики на зацикленность.
![\begin{align*}
&\text{begin} \\
&\text{for $X \in N$ do $\Gamma_x := 0$ end;}\\
&\text{for $T \in N$ do $\Gamma_x := \{A(X) \}$ end;}\\
&\text{\; \;$\{A(X)$ - граф со множеством вершин-множеством }\\
&\text{\; \;атрибутов символа $X$ и пустым множеством дуг\}}\\
&\text{\; \;finish := false; cycle := false;}\\
&\text{while (not finish) and (not cycle) do}\\
&\text{\; \; \; \; if ($\exists \; p : X_0$ $\rightarrow X_1 \ldots X_{np} ) \; \& \; (\exists \; G_i \in \Gamma_{x_i} , i \in [0, n_p] ) $ } \\
&\text{\; \; \; \; такие, что $D_p[G_1 \ldots Gn_p] $ содержит цикл}\\
&\text{\; \; \; \; then cycle := true}\\
&\text{\; \; \; \; else if ($\exists \; p : X_0$ $\rightarrow X_1 \ldots X_{np} ) \; \& \; (\exists \; G_i ( \Gamma_{x_i} , i \in [0, n_p] ) $ } \\
&\text{\; \; \; \; такие, что $D_p[G_1 \ldots Gn_p] \in \Gamma_{x0}$}\\
&\text{\; \; \; \; \; \; then $\Gamma_{x0}:=\Gamma_{x0} \; \{D_p[G_1 \ldots Gn_p]\}$}\\
&\text{\; \; \; \; \; \; else finish := true}\\
&\text{\; \;end end}\\
&\text{end end.}\\
\end{align*}](/sites/default/files/tex_cache/1a615c303183e5b3f9104c81217aeba6.png)
Теорема B.2. Атрибутная грамматика AG незациклена тогда и только тогда, когда ни один из графов Dp[G1 ... Gnp] не содержит ориентированных циклов, то есть когда алгоритм B.1. заканчивается со значением cycle = false.
Теорема B.3. Алгоритм Кнута проверки на зацикленность атрибутной грамматики размера n требует в общем случае exp(cn2) шагов.
