Программная система ПараЛаб для изучения и исследования методов параллельных вычислений

12.4.3. Матричное умножение

Задача умножения матрицы на матрицу определяется соотношениями:

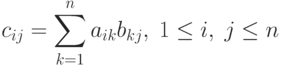
Основу возможности параллельных вычислений для матричного умножения составляет независимость расчетов для получения элементов с_ij результирующей матрицы C. Тем самым, все элементы матрицы C могут быть вычислены параллельно при наличии n² процессоров, при этом на каждом процессоре будет располагаться по одной строке матрицы A и одному столбцу матрицы B. При меньшем количестве процессоров подобный подход приводит к ленточной схеме разбиения данных, когда на процессорах располагаются по несколько строк и столбцов (полос) исходных матриц.

Другой широко используемый подход для построения параллельных способов выполнения матричного умножения состоит в применении блочного представления матриц, при котором исходные матрицы A, B и результирующая матрица C рассматриваются в виде наборов блоков (как правило, квадратного вида некоторого размера mxm ). Тогда операцию матричного умножения матриц A и B в блочном виде можно представить следующим образом:

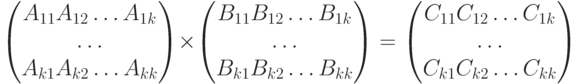
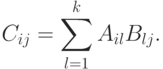
Полученные блоки C_ij также являются независимыми, и, как результат, возможный подход для параллельного выполнения вычислений может состоять в расчетах, связанных с получением отдельных блоков C_ij, на разных процессорах. Применение подобного подхода позволяет получить многие эффективные параллельные методы умножения блочно-представленных матриц.

В системе ПараЛаб реализованы параллельный алгоритм умножения матриц при ленточной схеме разделения данных и два метода ( алгоритмы Фокса и Кэннона ) для блочно представленных матриц. Более полная информация об алгоритмах умножения матриц, реализованных в системе ПараЛаб, содержится в "Параллельные методы матричного умножения" .

12.4.3.1. Ленточный алгоритм

При ленточной схеме разделения данных исходные матрицы разбиваются на горизонтальные (для матрицы A ) и вертикальные (для матрицы B ) полосы. Получаемые полосы распределяются по процессорам, при этом на каждом из имеющегося набора процессоров располагается только по одной полосе матриц A и B. Перемножение полос (а данная операция может быть выполнена процессорами параллельно) приводит к получению части блоков результирующей матрицы C. Для вычисления оставшихся блоков матрицы C сочетания полос матриц A и B на процессорах должны быть изменены. В наиболее простом виде это может быть обеспечено, например, при кольцевой топологии вычислительной сети (при числе процессоров, равном количеству полос) – в этом случае необходимое для матричного умножения изменение положения данных может быть реализовано циклическим сдвигом полос матрицы B по кольцу. После многократного выполнения описанных действий (количество необходимых повторений является равным числу процессоров) на каждом процессоре получается набор блоков, образующий горизонтальную полосу матрицы C.

Рассмотренная схема вычислений позволяет определить параллельный алгоритм матричного умножения при ленточной схеме разделения данных как итерационную процедуру, на каждом шаге которой происходит параллельное выполнение операции перемножения полос и последующего циклического сдвига полос одной из матриц по кольцу. Подробное описание ленточного алгоритма приводится в "Параллельные методы матричного умножения" .

Задания и упражнения

1. Создайте в системе ПараЛаб новое окно вычислительного эксперимента. Для этого окна выберите задачу матричного умножения (щелкните левой кнопкой мыши на строке Матричное умножение пункта меню Задача ).
2. Откройте диалоговое окно выбора метода и убедитесь в том, что выбран метод ленточного умножения матриц.
3. Проведите несколько вычислительных экспериментов. Изучите зависимость времени выполнения алгоритма от объема исходных данных и от количества процессоров.

12.4.3.2. Блочные алгоритмы Фокса и Кэннона

При блочном представлении данных параллельная вычислительная схема матричного умножения в наиболее простом виде может быть построена, если топология вычислительной сети имеет вид прямоугольной решетки (если реальная топология сети имеет иной вид, представление сети в виде решетки можно обеспечить на логическом уровне). Основные положения параллельных методов для блочно представленных матриц состоят в следующем:

1. каждый из процессоров решетки отвечает за вычисление одного блока матрицы C ;
2. в ходе вычислений на каждом из процессоров располагается по одному блоку исходных матриц A и В ;
3. при выполнении итераций алгоритмов блоки матрицы А последовательно сдвигаются вдоль строк процессорной решетки, а блоки матрицы B — вдоль столбцов решетки;
4. в результате вычислений на каждом из процессоров получается блок матрицы С, при этом общее количество итераций алгоритма равно 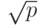(где р – число процессоров).

В "Параллельные методы матричного умножения" приводится полное описание параллельных методов Фокса и Кэннона для умножения блочно-представленных матриц.

Задания и упражнения

• В активном окне вычислительного эксперимента системы ПараЛаб установите топологию Решетка. Выберите число процессоров, равное девяти. Сделайте текущей задачей этого окна задачу матричного умножения.
• Выберите метод Фокса умножения матриц и проведите вычислительный эксперимент.
• Выберите алгоритм Кэннона матричного умножения и выполните вычислительный эксперимент. Пронаблюдайте различные маршруты передачи данных при выполнении алгоритмов. Сравните временные характеристики алгоритмов.
• Измените число процессоров в топологии Решетка на шестнадцать. Последовательно выполните вычислительные эксперименты с использованием метода Фокса и метода Кэннона. Сравните временные характеристики этих экспериментов.

12.4.4. Решение систем линейных уравнений

Системы линейных уравнений возникают при решении ряда прикладных задач, описываемых системами нелинейных (трансцендентных), дифференциальных или интегральных уравнений. Они могут появляться также в задачах математического программирования, статистической обработки данных, аппроксимации функций, при дискретизации краевых дифференциальных задач методом конечных разностей или методом конечных элементов и т.д.

Линейное уравнение с n неизвестными x₀, x₁, ..., x_n-1 может быть определено при помощи выражения

a0x0+a1x1+...+an-1xn-1=b,

где величины a₀, a₁, ..., a_n-1 и b представляют собой постоянные значения.

Множество n линейных уравнений

a0,0x0   + a0,1x1   + ... + a0,n-1xn-1   = b0
a1,0x0   + a1,1x1   + ... + a1,n-1xn-1   = b1
 . . .
an-1,0x0  + an-1,1x1 + ... + an-1,n-1xn-1  = bn-1

называется системой линейных уравнений или линейной системой. В более кратком (матричном) виде система может быть представлена как

Ax=b,

где A=(a_i,j) есть вещественная матрица размера nxn, а векторы b и x состоят из n элементов.

Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b понимается нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.

В системе ПараЛаб реализованы два алгоритма решения систем линейных уравнений: широко известный метод Гаусса (прямой метод решения систем линейных уравнений, находит точное решение системы с невырожденной матрицей за конечное число шагов) и метод сопряженных градиентов – один из широкого класса итерационных методов решения систем линейных уравнений с матрицей специального вида. Более полная информация об алгоритмах решения систем линейных уравнений, реализованных в системе ПараЛаб, содержится в "Решение систем линейных уравнений" .

12.4.4.1. Алгоритм Гаусса

Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейный уравнений при помощи последовательного исключения неизвестных (при помощи эквивалентных преобразований) приводится к верхнему треугольному виду. На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д.

При внимательном рассмотрении метода Гаусса можно заметить, что все вычисления сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Как результат, в основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. В этом случае матрицу А можно разделить на горизонтальные полосы, а вектор правых частей b – на блоки. Полосы матрицы и блоки вектора правых частей распределяются между процессорами вычислительной системы.

Для выполнения прямого хода метода Гаусса необходимо осуществить (n-1) итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду.

Выполнение итерации i, 0<=i<n-1, прямого хода метода Гаусса включает ряд последовательных действий. Процессор, на котором расположена строка i матрицы, должен разослать ее и соответствующий элемент вектора b всем процессорам, которые содержат строки с номерами k, k>i. Получив ведущую строку, процессоры выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной x_i.

При выполнении обратного хода метода Гаусса процессоры выполняют необходимые вычисления для нахождения значения неизвестных. Как только какой-либо процессор определяет значение своей переменной x_i, это значение должно быть разослано всем процессорам, которые содержат строки с номерами k, k<i. Далее процессоры подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора b.

Задания и упражнения

1. В активном окне вычислительного эксперимента системы ПараЛаб установите топологию Полный граф. Выберите число процессоров, равное десяти. Сделайте текущей задачей этого окна задачу решения системы линейных уравнений.
2. Выберите метод Гаусса решения задачи и выполните вычислительный эксперимент. Пронаблюдайте маршруты передачи данных при выполнении алгоритма.