Программная система ПараЛаб для изучения и исследования методов параллельных вычислений

12.4.1. Сортировка данных

Сортировка является одной из типовых проблем обработки данных и обычно понимается как задача размещения элементов неупорядоченного набора значений

S={a1,a2,...,an}

в порядке монотонного возрастания или убывания

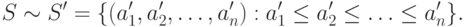
Вычислительная трудоемкость процедуры упорядочивания является достаточно высокой. Так, для ряда известных простых методов (пузырьковая сортировка, сортировка включением и др.) количество необходимых операций определяется квадратичной зависимостью от числа упорядочиваемых данных

T1~n2.

Для более эффективных алгоритмов ( сортировка слиянием, сортировка Шелла, быстрая сортировка ) трудоемкость определяется величиной

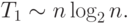
Данное выражение дает также нижнюю оценку необходимого количества операций для упорядочивания набора из n значений; алгоритмы с меньшей трудоемкостью могут быть получены только для частных вариантов задачи.

Ускорение сортировки может быть обеспечено при использовании нескольких (p, p>1) процессоров. Исходный упорядочиваемый набор в этом случае разделяется между процессорами; в ходе сортировки данные пересылаются между процессорами и сравниваются между собой. Результирующий (упорядоченный) набор, как правило, также разделен между процессорами, при этом для систематизации такого разделения для процессоров вводится та или иная система последовательной нумерации и обычно требуется, чтобы при завершении сортировки значения, располагаемые на процессорах с меньшими номерами, не превышали значений процессоров с большими номерами.

В системе ПараЛаб в качестве методов упорядочения данных представлены пузырьковая сортировка, сортировка Шелла, быстрая сортировка. Исходные (последовательные) варианты этих методов изложены во многих изданиях (см., например, [ [ 26 ] ]), способы их параллельного выполнения приводятся в "Параллельные методы сортировки" .

12.4.1.1. Пузырьковая сортировка

Алгоритм пузырьковой сортировки в прямом виде достаточно сложен для распараллеливания — сравнение пар соседних элементов происходит строго последовательно. Параллельный вариант алгоритма основывается на методе чет-нечетной перестановки, для которого на нечетной итерации выполнения сравниваются элементы пар

(a1,a2),(a3,a4),...,(an–1,an).

Если пара не упорядочена, то ее элементы переставляются. На четной итерации упорядочиваются пары

(a2,a3),(a4,a5),...,(an–2,an–1).

После n -кратного повторения подобных итераций массив оказывается отсортированным. Более подробная информация о параллельном варианте алгоритма приводится в "Параллельные методы сортировки" .

Задания и упражнения

1. Запустите систему ПараЛаб и создайте новый эксперимент. Выберите пункт меню Задача и убедитесь, что в активном окне текущей задачей является задача сортировки. Откройте диалоговое окно выбора метода и посмотрите, какие алгоритмы сортировки могут быть выполнены на текущей топологии. Так как при создании эксперимента по умолчанию текущей топологией становится кольцо, то единственный возможный алгоритм – алгоритм сортировки пузырьком. Закройте диалоговое окно и вернитесь в основное меню системы ПараЛаб.
2. Выполните несколько экспериментов, изменяя размер исходных данных. Для выполнения эксперимента выполните команду В активном окне пункта меню Выполнить. Проанализируйте временные характеристики экспериментов, которые отображаются в правой нижней части окна.
3. Проведите несколько вычислительных экспериментов, изменяя количество процессоров вычислительной системы. Проанализируйте полученные временные характеристики.

12.4.1.2. Сортировка Шелла

Параллельный алгоритм сортировки Шелла может быть получен как обобщение метода параллельной пузырьковой сортировки. Основное различие состоит в том, что на первых итерациях алгоритма Шелла происходит сравнение пар элементов, которые в исходном наборе данных находятся далеко друг от друга (для упорядочивания таких пар в пузырьковой сортировке может понадобиться достаточно большое количество итераций). Подробное описание параллельного обобщения алгоритма сортировки Шелла можно найти в лекции 9.

Задания и упражнения

1. Запустите систему ПараЛаб. Выберите топологию кольцо и установите количество процессоров, равное восьми. Проведите эксперимент по выполнению алгоритма пузырьковой сортировки.
2. Установите в окне вычислительного эксперимента топологию гиперкуб и число процессоров, равное восьми.
3. Откройте диалоговое окно выбора метода и посмотрите, какие алгоритмы сортировки могут быть выполнены на этой топологии. Выберите метод сортировки Шелла. Закройте окно.
4. Проведите вычислительный эксперимент. Сравните количество итераций, выполненных при решении задачи при помощи метода Шелла, с количеством итераций алгоритма пузырьковой сортировки (количество итераций отображается справа в строке состояния). Убедитесь в том, что при выполнении эксперимента с использованием алгоритма Шелла для сортировки массива необходимо выполнить меньшее количество итераций.
5. Проведите эксперимент с использованием метода Шелла несколько раз. Убедитесь, что количество итераций не является постоянной величиной и зависит от исходного массива.

12.4.1.3. Быстрая сортировка

Алгоритм быстрой сортировки основывается на последовательном разделении сортируемого набора данных на блоки меньшего размера таким образом, что между значениями разных блоков обеспечивается отношение упорядоченности. При параллельном обобщении алгоритма обеспечивается отношение упорядоченности между элементами сортируемого набора, расположенными на процессорах, соседних в структуре гиперкуба. В материалах "Параллельные методы сортировки" вы можете найти подробное описание алгоритма быстрой сортировки.

Задания и упражнения

1. Запустите систему ПараЛаб. В появившемся окне вычислительного эксперимента установите топологию гиперкуб и количество процессоров, равное восьми.
2. Выполните три последовательных эксперимента с использованием трех различных алгоритмов сортировки: сортировки пузырьком, сортировки Шелла и быстрой сортировки. Сравните временные характеристики алгоритмов, которые отображаются в правой нижней части окна. Убедитесь в том, что у быстрой сортировки наименьшее время выполнения алгоритма и время передачи данных.
3. Измените объем исходных данных (выполните команду Параметры задачи пункта меню Задача ). Снова проведите эксперименты. Сравните временные характеристики алгоритмов.
4. Измените количество процессоров (выполните команду Количество процессоров пункта меню Система ). Проведите вычислительные эксперименты и сравните временные характеристики.