Параллельные методы на графах

10.3.4. Комбинаторные методы

В отличие от геометрических методов, комбинаторные алгоритмы (см., например, [ [ 36 ] , [ 67 ] ]) обычно оперируют не с сетью, а с графом, построенным для этой сети. Соответственно, в отличие от геометрических схем, комбинаторные методы не принимают во внимание информацию о близости расположения элементов сети друг относительно друга, руководствуясь только смежностью вершин графа. Комбинаторные методы обычно обеспечивают более сбалансированное разбиение и меньшее информационное взаимодействие полученных подсетей. Однако комбинаторные методы имеют тенденцию работать существенно дольше, чем их геометрические аналоги.

10.3.4.1. Деление с учетом связности

С самых общих позиций понятно, что при разделении графа информационная зависимость между разделенными подграфами будет меньше, если соседние вершины (вершины, между которыми имеются дуги) будут находиться в одном подграфе. Алгоритм деления графов с учетом связности ( the levelized nested dissection algorithm ) пытается достичь этого, последовательно добавляя к формируемому подграфу соседей. На каждой итерации алгоритма происходит разделение графа на 2 части. Таким образом, разделение графа на требуемое число частей достигается путем рекурсивного применения алгоритма.

Общая схема алгоритма может быть описана при помощи следующего набора правил.

Алгоритм 10.2. Общая схема выполнения алгоритма деления графов с учетом связности

• Iteration = 0.
• Присвоение номера Iteration произвольной вершине графа.
• Присвоение ненумерованным соседям вершин с номером Iteration номера Iteration + 1.
• Iteration = Iteration + 1.
• Если еще есть неперенумерованные соседи, то переход на шаг 3.
• Разделение графа на 2 части в порядке нумерации.

Для минимизации информационных зависимостей имеет смысл в качестве начальной выбирать граничную вершину. Поиск такой вершины можно осуществить методом, близким к рассмотренной схеме. Так, перенумеровав вершины графа в соответствии с алгоритмом 10.2 (начиная нумерацию из произвольной вершины), мы можем взять любую вершину с максимальным номером. Как нетрудно убедиться, она будет граничной.

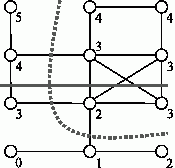
Пример работы алгоритма приведен на рис. 10.15. Цифрами показаны номера, которые получили вершины в процессе разделения. Сплошной линией показана граница, разделяющая 2 подграфа. Также на рисунке показано лучшее решение (пунктирная линия). Очевидно, что полученное алгоритмом разбиение далеко от оптимального, так как в приведенном примере есть решение только с тремя пересеченными ребрами вместо пяти.

Рис. 10.15. Пример работы алгоритма деления графов с учетом связности

10.3.4.2. Алгоритм Кернигана – Лина

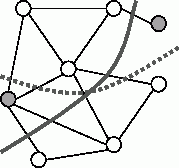
В алгоритме Кернигана – Лина ( the Kernighan – Lin algorithm ) используется несколько иной подход для решения проблемы оптимального разбиения графа – предполагается, что некоторое начальное разбиение графа уже существует, затем имеющееся приближение улучшается в течение некоторого количества итераций. Применяемый способ улучшения в алгоритме Кернигана – Лина состоит в обмене вершинами между подмножествами имеющегося разбиения графа (см. рис. 10.16). Для формирования требуемого количества частей графа может быть использована, как и ранее, рекурсивная процедура деления пополам.

Общая схема одной итерации алгоритма Кернигана – Лина может быть представлена следующим образом.

Алгоритм 10.3. Общая схема алгоритма Кернигана – Лина

• Формирование множества пар вершин для перестановки. Из вершин, которые еще не были переставлены на данной итерации, формируются все возможные пары (в парах должно присутствовать по одной вершине из каждой части имеющегося разбиения графа ).
• Построение новых вариантов разбиения графа. Каждая пара, подготовленная на шаге 1, поочередно используется для обмена вершин между частями имеющегося разбиения графа для получения множества новых вариантов деления.
• Выбор лучшего варианта разбиения графа. Для сформированного на шаге 2 множества новых делений графа выбирается лучший вариант. Этот вариант далее фиксируется как новое текущее разбиение графа, а соответствующая выбранному варианту пара вершин отмечается как использованная на текущей итерации алгоритма.
• Проверка использования всех вершин. При наличии в графе вершин, еще не использованных при перестановках, выполнение итерации алгоритма снова продолжается с шага 1. Если же перебор вершин графа завершен, далее следует шаг 5.
• Выбор наилучшего варианта разбиения графа. Среди всех разбиений графа, полученных на шаге 3 проведенных итераций, выбирается (и фиксируется) наилучший вариант разбиения графа.

Поясним дополнительно, что на шаге 2 итерации алгоритма перестановка вершин каждой очередной пары осуществляется для одного и того же разбиения графа, выбранного до начала выполнения итерации или определенного на шаге 3. Общее количество выполняемых итераций, как правило, фиксируется заранее и является параметром алгоритма (за исключением случая остановки при отсутствии улучшения разбиения на очередной итерации).

Рис. 10.16. Пример перестановки двух вершин (выделены серым) в методе Кернигана – Лина

10.3.5. Сравнение алгоритмов разбиения графов

Рассмотренные алгоритмы разбиения графов различаются точностью получаемых решений, временем выполнения и возможностями для распараллеливания (под точностью понимается величина близости получаемых при помощи алгоритмов решений к оптимальным вариантам разбиения графов ). Выбор наиболее подходящего алгоритма в каждом конкретном случае является достаточно сложной и неочевидной задачей. Проведению такого выбора может содействовать сведенная воедино в табл. 10.5 (см. [ [ 67 ] ]) общая характеристика ряда алгоритмов разделения графов, рассмотренных в данном разделе. Дополнительная информация по проблеме оптимального разбиения графов может быть получена, например, в [ [ 67 ] ].

Таблица 10.5. Сравнительная таблица некоторых алгоритмов разделения графов

Алгоритмы		Необходимость координатной информации	Точность	Время выполнения	Возможности для распараллеливания
Покоординатное разбиение		Да
Рекурсивный инерционный метод деления пополам		Да
Деление с учетом связности		Нет
Алгоритм Кернигана - Лина	1 итерация	Нет
	10 итераций	Нет
	50 итераций	Нет

Столбец "Необходимость координатной информации" отмечает использование алгоритмом координатной информации об элементах сети или вершинах графа.

Столбец "Точность" дает качественную характеристику величины приближения получаемых алгоритмом решений к оптимальным вариантам разбиения графов. Каждый дополнительный закрашенный кружок определяет примерно 10%-процентное улучшение точности приближения.

Столбец "Время выполнения" показывает относительное время, затрачиваемое различными алгоритмами разбиения. Каждый дополнительный закрашенный кружок соответствует увеличению времени разбиения примерно в 10 раз.

Столбец "Возможности для распараллеливания" характеризует свойства алгоритмов для параллельного выполнения. Алгоритм Кернигана – Лина при выполнении только одной итерации почти не поддается распараллеливанию. Этот же алгоритм при большем количестве итераций, а также метод деления с учетом связности могут быть распараллелены со средней эффективностью. Алгоритм покоординатного разбиения и рекурсивный инерционный метод деления пополам обладают высокими показателями для распараллеливания.