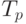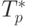Решение систем линейных уравнений
8.3.3. Анализ эффективности
Выберем для дальнейшего анализа эффективности получаемых параллельных вычислений параллельный алгоритм матрично-векторного умножения при ленточном горизонтальном разделении матрицы и при полном дублировании всех обрабатываемых векторов.
Трудоемкость последовательного метода сопряженных градиентов была уже определена ранее в (8.12).
Определим время выполнения параллельной реализации метода сопряженных градиентов. Вычислительная сложность параллельных операций умножения матрицы на вектор при использовании схемы ленточного горизонтального разделения матрицы составляет:
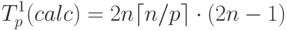
Как результат, при условии дублирования всех вычислений над векторами общая вычислительная сложность параллельного варианта метода сопряженных градиентов равна:
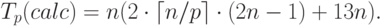
С учетом полученных оценок показатели ускорения и эффективности параллельного алгоритма могут быть выражены при помощи соотношений:
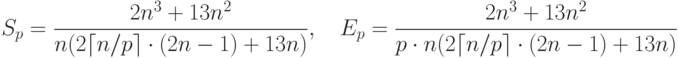
Рассмотрев построенные показатели, можно отметить, что балансировка вычислительной нагрузки между процессорами в целом является достаточно равномерной.
Уточним теперь приведенные выражения – учтем длительность выполняемых вычислительных операций и оценим трудоемкость операции передачи данных между процессорами. Как можно заметить, информационное взаимодействие процессоров возникает только при выполнении операций умножения матрицы на вектор. С учетом результатов лекции 6 коммуникационная сложность рассматриваемых параллельных вычислений равна:
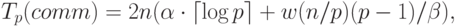
 – латентность,
– латентность,  – пропускная способность сети
передачи данных, а w есть размер элемента упорядочиваемых данных
в байтах.
– пропускная способность сети
передачи данных, а w есть размер элемента упорядочиваемых данных
в байтах.Окончательно, время выполнения параллельного варианта метода сопряженных градиентов для решения систем линейных уравнений принимает вид:
![T_p=n\cdot[(2\lceil n/p\rceil\cdot(2n-1)+13n)\cdot\tau+2(\alpha\cdot\lceil\log p\rceil+w(n/p)(p-1)/ \beta)]](/sites/default/files/tex_cache/49e8369ef90e43b53ffc668b962a166c.png) |
( 8.13) |
 есть время выполнения базовой вычислительной операции.
есть время выполнения базовой вычислительной операции.8.3.4. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта метода сопряженных градиентов для решения систем линейных уравнений проводились при условиях, указанных в п. 8.2.7.
Результаты вычислительных экспериментов приведены в таблице 8.3. Эксперименты проводились на вычислительных системах, состоящих из двух, четырех и восьми процессоров.
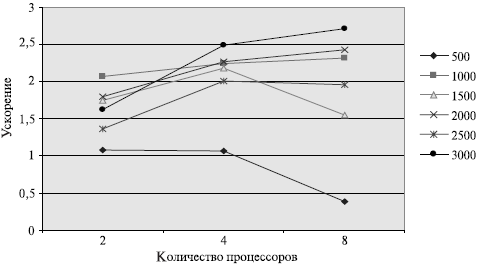
Рис. 8.6. Зависимость ускорения от количества процессоров при выполнении параллельного метода сопряженных градиентов для решения систем линейных уравнений
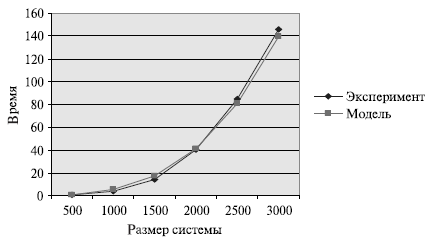
Сравнение времени выполнения эксперимента 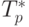 и теоретической
оценки Tp из (8.13) приведено в таблице 8.4 и на рис. 8.7.
и теоретической
оценки Tp из (8.13) приведено в таблице 8.4 и на рис. 8.7.