Нейронные сети, как способ обработки данных
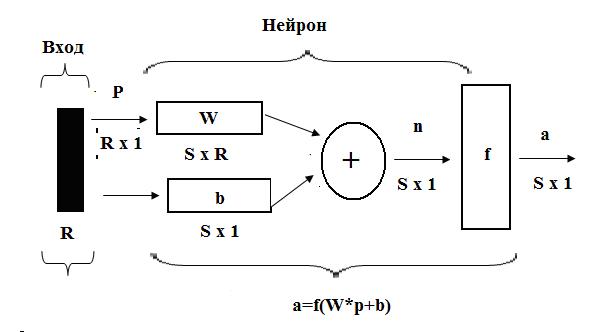
Для однослойной нейронной сети рассмотрим процесс функционирования более подробно. Каждый элемент вектора входа соединен со всеми входами нейрона и это соединение задается матрицей весов W; при этом каждый 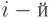 нейрон включает суммирующий элемент, который формирует скалярный выход
нейрон включает суммирующий элемент, который формирует скалярный выход 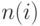 . Совокупность скалярных функций
. Совокупность скалярных функций 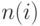 объединяются в
объединяются в  – элементный вектор входа
– элементный вектор входа  функции активации слоя. Выходы слоя нейронов формируют вектор столбец а, и таким образом описание слоя нейтронов имеет вид
функции активации слоя. Выходы слоя нейронов формируют вектор столбец а, и таким образом описание слоя нейтронов имеет вид 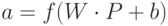 и описывает одиночный маршрут. Структурная схема однослойной нейронной сети представлена на Рисунке 10.8, здесь
и описывает одиночный маршрут. Структурная схема однослойной нейронной сети представлена на Рисунке 10.8, здесь  – вектор входа
– вектор входа  ,
,  – весовая матрица
– весовая матрица 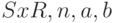 векторы размера
векторы размера  .
.
На данном этапе разработки аналитическим способом подобраны оптимальные значения факторов. По количеству факторов определено число нейронов в сети. Модель нейронной сети выбирает образ из набора, который содержится в её памяти.
НС представляет собой адаптивную систему, жизненный цикл которой состоит из двух независимых фаз – обучения и работы сети.
Обучение сети состоит в поиске вектора  , для которого суммарная ошибка по всем маршрутам минимальна:
, для которого суммарная ошибка по всем маршрутам минимальна:
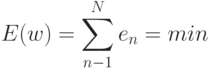 |
( 10.8) |
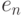 - ошибка для
- ошибка для  - маршрута.
- маршрута.
Для исследования процесса маршрутизации в вычислительных сетях используем нейронные сети прямого распространения с частичной структурой связей.
Обучение — это процесс, в результате которого система постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация — это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий.
Кроме того, результат самообучения характеризует пригодность выбранного пространства для конкретной задачи обучения распознаванию. Если абстрактные образы, выделяемые в процессе самообучения, совпадают с реальными, то пространство выбрано удачно. Чем сильнее абстрактные образы отличаются от реальных, тем "неудобнее" выбранное пространство для конкретной задачи.
Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится так:
- Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигналы распространяются от входов к выходам, рассчитать значения последних.
где
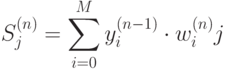
( 10.9)  – число нейронов в слое
– число нейронов в слое 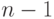 с учетом нейрона с постоянным выходным состоянием +1, задающего смещение;
с учетом нейрона с постоянным выходным состоянием +1, задающего смещение; 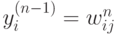 – i-ый вход нейрона
– i-ый вход нейрона  слоя
слоя  .
где
.
где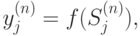
( 10.10)  -сигмоиддальная функция
где
-сигмоиддальная функция
где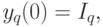
( 10.11) 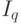 - q-я компонента вектора входного образа.
- q-я компонента вектора входного образа.
- Скорректировать все веса в НС
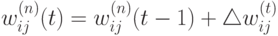
( 10.11) - Если ошибка сети существенна, перейти на шаг 1. В противном случае – конец.
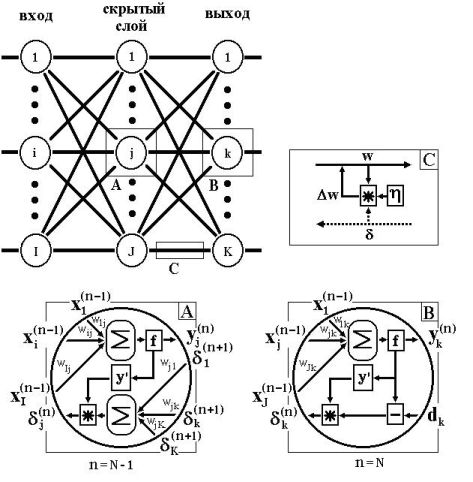
Сети на шаге 1 попеременно в случайном порядке предъявляются все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других. Алгоритм иллюстрируется на рисунке 10.9.
В процессе обучения линейной сети траектория будет перемещаться из начальной точки в точку минимума критерия качества.