Нейронные сети, как способ обработки данных

Однослойные искусственные нейронные сети

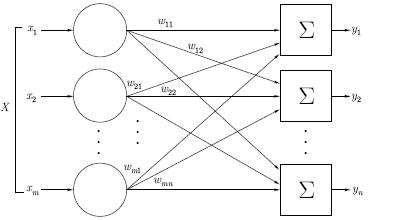
Хотя один нейрон и способен выполнять простейшие процедуры распознавания, но для серьезных нейронных вычислений необходимо соединять нейроны в сети. Простейшая сеть состоит из группы нейронов, образующих слой, как показано в правой части рисунка ( см. Рисунок 10.4). Вершины-круги слева служат лишь для распределения входных сигналов. Они не выполняют каких-либо вычислений, и поэтому не будут считаться слоем. Для большей наглядности обозначим их кругами, чтобы отличать их от вычисляющих нейронов, обозначенных квадратами. Каждый элемент из множества входов отдельным весом соединен с каждым искусственным нейроном. каждый нейрон выдает взвешенную сумму входов в сеть. В искусственных и биологических сетях многие соединения могут отсутствовать, но здесь они показаны все для демонстрации общей картины. Могут существовать также соединения между выходами и входами элементов в слое [4].

Рис. 10.4. Простейшая нейронная сеть

Удобно считать веса элементами матрицы W. Матрица имеет строк и столбцов, где — число входов, а — число нейронов. Например, 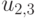— это вес, связывающий второй вход с третьим нейроном. Таким образом, вычисление выходного вектора , компонентами которого являются выходы 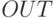нейронов, сводится к матричному умножению 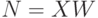, где и — векторы-строки.

Построение универсальных моделей нейросетей в составе программного обеспечения компьютера, снабженных механизмами приспособления под задачу пользователя задача современной действительности. Еще более актуально построить набор аппаратных средств – нейросетей, сопряженных с компьютером и, по выбору пользователя, участвующих в решении сложных задач. Такие аппаратно реализованные нейросети, как приставки или внешние устройства компьютера, например, определяют специальное направление использования ПЛИС (programmable logic device программируемая интегральная схема) - интегральных схем с программируемой логикой.

Если рассматривать сеть, то необходимо принимать во внимание то, что, во-первых, предложенное решение должно учитывать текущее состояние сети, качество связи и наличие критических участков, а во-вторых, поиск оптимального решения должен осуществляться в реальном времени. Выбор маршрутов, максимизирующих степень узла в сети, предоставляет возможность планирования работы сети таким образом, чтобы время пересылки пакета по сети было бы минимальным. Степень узла определяется как сумма всех потоков, поступающих в узел и исходящих от узла. Критерий качества работы, который выбирается для задач маршрутизации, должен отражать цели, связанные с соответствующей задачей, составления плана работы линий связи. Требуется выбрать маршрут между парой источник – приемник с таким расчетом, чтобы минимизировать критерий качества работы. Показатель качества работы должен согласовываться со структурой нейронной сети.

Рассмотрим пример применения НС для предсказания прохождения пакетов по сети.

С каждой такой нейронной сетью связан потоковый граф, вершины которого соответствуют нейронам, а также входам и выходам сети, а дуги – связям. Пусть - множество вершин сети, тогда множество дуг является подмножеством , т.е. каждой дуге соответствует упорядоченная пара вершин 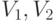из первой дуга исходит, а во вторую – входит. Каждой вершине сопоставим активационную функцию 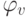, каждой дуге 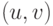– вес 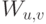. Сеть прямого распространения не имеет циклов, т.е. её вершины всегда можно пронумеровать так (т.е. можно считать множеством натуральных чисел), что 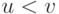для каждой дуги.

Обозначим 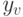вход соответствующего вершине с номером нейрона, а 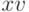- его выход. Тогда указанная нейронная сеть описывается соотношением

( 10.6)

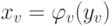( 10.7)

Для большинства архитектур нейронных сетей отображение 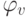действует покоординатно и определяется функцией активации соответствующего нейрона. Недостатком таких сетей является, невозможность рассмотрения процедуры их модификации, работающие на уровне отдельных связей.

Для исследований выбираем архитектуру сети: линейную нейронную сеть с линией задержки по входу на 4 такта, с одним входом. Алгоритм управления потоками в этой сети состоит в следующем. В течение некоторого времени гипотетический прибор собирает информацию о состоянии сети. На вход нейронной сети, с одним слоем и числом нейронов n поступает некая информация, в соответствии, с которой сеть, находит образ на выходе и устанавливается в состояние равновесия. Данные для моделирования сети возьмем из предыдущего раздела. Значения входной переменной обозначим как массив P={[1;5,4] [2;4,7] [3;2,9] [4;1,8]}, первое значение это количество переходов, второе значение это скорость передачи информации и массив цели T={1,84;1,49;0,37;0,1} время прохождения информации по сети. Обучающая последовательность time=0:0.1:1

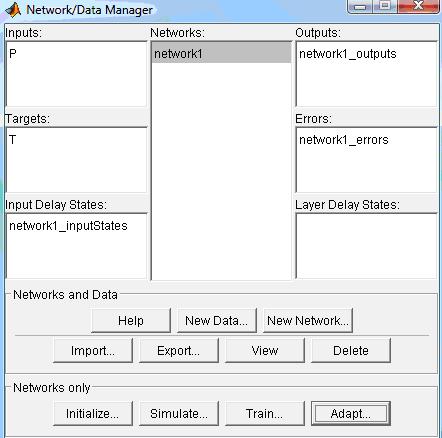
Проектируем сеть с помощью MATLAB (см. Рисунок 10.5).

Рис. 10.5. Окно управления сетью

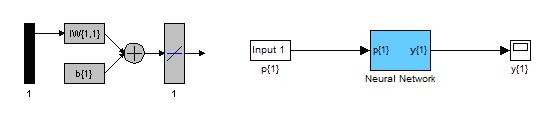
Последовательность входов и целей представлены на Рисунке 10.4 исходя из этих данных моделируем нейронную сеть. Имитационная модель нейронной сети представлена на рисунке 10.6.

Рис. 10.6. Модель нейронной сети

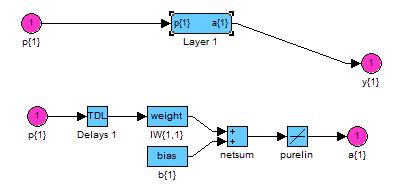
Имитационную модель рассмотрим в системе Simulink. Эта схема в данном пакете является в полной мере функциональной. Функциональная схема модели нейронной сети представлена на рисунке 10.7.

Рис. 10.7.