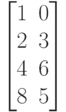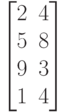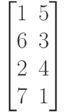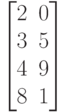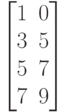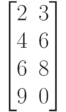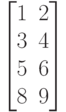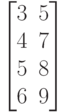Статистическая обработка в Mathcad
Подготовка к работе
По указанной литературе изучить приёмы работы с формулами, функциями, форматирование и редактирование данных.
Контрольные вопросы
- Что такое ранжированная переменная и для решения, каких задач она используется?
- Какие категории функций имеются в системе MathCAD?
- Дать понятие функции пользователя?
- Назовите виды операторов системы MathCAD и поясните их назначение.
- Как вывести результаты вычислений в виде таблиц?
- Организация вложенных циклов.
- Правила задания многомерных функций.
Задания на выполнение
Научиться использовать математические и статистические функции в системе MathCAD.
-
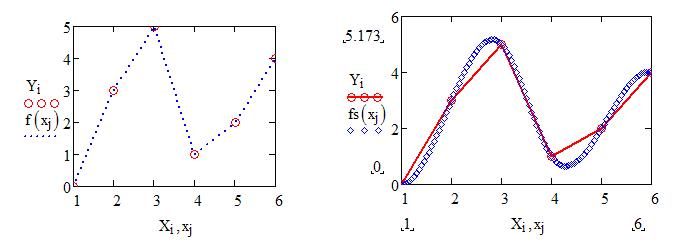
Линейная и сплайновая интерполяции.
Исходные данные для выполнения задания 1 в таблице 2.1.
Рассмотрим линейную интерполяциюЛинейная интерполяция
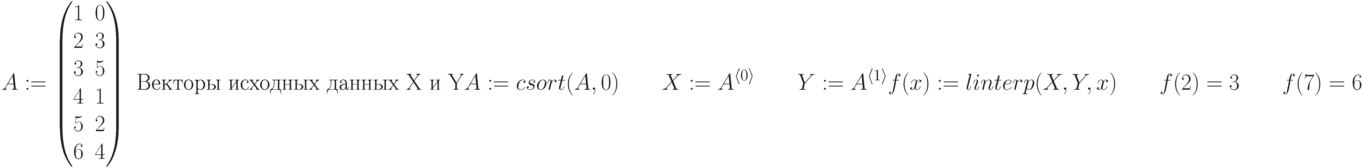
Сплайновая интерполяция
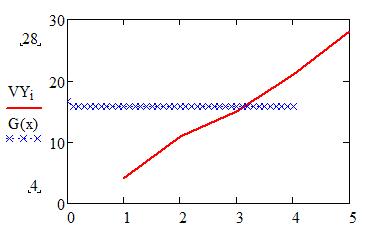
Как мы видим значения точек при линейной и сплайновой интерполяции различны.
Построим графики линейной и сплайновой интерполяций. Для этого задается количество точек и шаг.
-
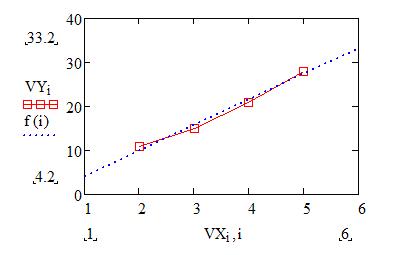
Линейная регрессия.
Исходные данные для выполнения задания 2 в таблице 4.2.
Таблица 4.2. № Заданные вектора № Заданные вектора 1 VX=[3, 2, 4, 5] 4 VX=[7, 18, 3, 11] VY=[7, 8, 9, 5] VY=[1, 5, 3, 9] 2 VX=[12, 14, 7, 11] 5 VX=[24, 9, 12, 27] VY=[6, 8, 10, 15] VY=[9, 3, 17, 11] 3 VX=[3, 9, 12, 14] 6 VX=[4, 15, 2, 19] VY=[7, 9, 11, 13] VY=[11, 17, 1, 13] 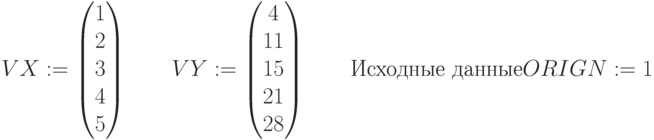
Вычислим коэффициенты a и b линейной регрессии
По этим данным строим график линейной регрессии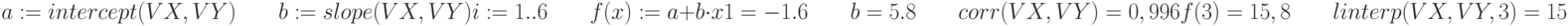
-
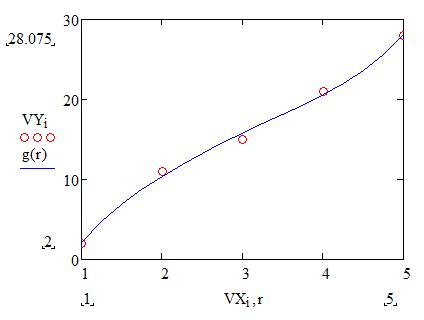
Линейная регрессия общего вида.
Исходные данные для выполнения задания 3 в таблице 4.2.
Функции F(x) подбираются так, чтобы коэффициент детерминации стремился к единице.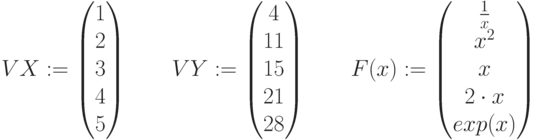
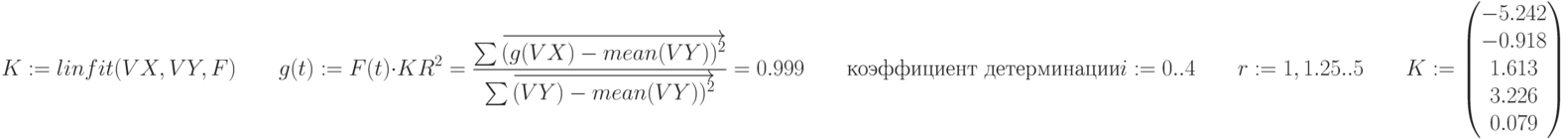
g(t) – это функция регрессии
К – коэффициент функции регрессии
-
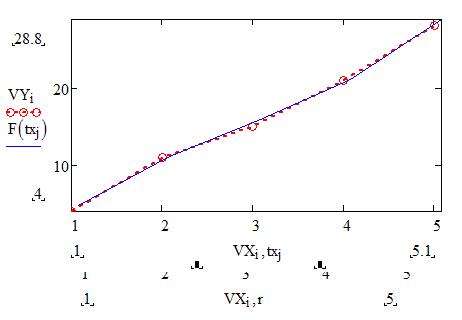
Полиномиальная регрессия
Исходные данные для выполнения задания 4 в таблице 4.2.
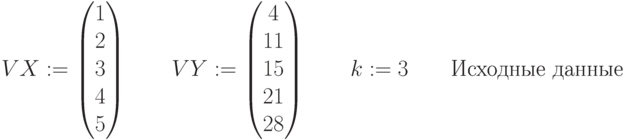
k – степень полинома, от него зависит насколько точно будет построена функция.
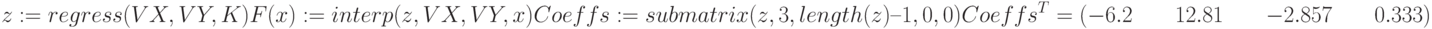
F(x) - выдаёт интерполированное значение в x от коэффициентов вектора напротив, и оригинальных данных в VX и VY.
Coeffs - выдаёт субматрицу массива состоящую из элементов в строках ir через jr и столбцах ic через jc из z.
CoeffsT - преобразует коэффициент в горизонтальную запись

-
Нелинейная регрессия общего вида.
Исходные данные для выполнения задания 5 в таблице 4.2
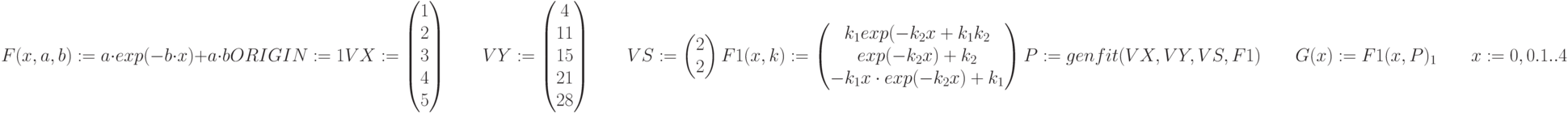 Вектор
Вектор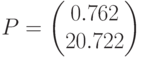
 возращает значения
возращает значения 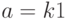 и
и 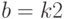 для наилучшего среднеквадратического приближения
для наилучшего среднеквадратического приближения 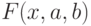
В заключение работы, следует сделать вывод о целесообразности применения той или иной регрессии, чем они друг от друга отличаются.