Арифметичность вычислимых функций
Более тонкий анализ позволяет установить, что для любой
достаточно богатой формальной системы (скажем, для формальной
арифметики или теории множеств) множество доказуемых формул
(теорем) и множество опровержимых формул (отрицания которых
являются теоремам) являются перечислимыми эффективно
неотделимыми множествами. Это
делается
примерно так. Рассмотрим два произвольных непересекающихся
перечислимых множества A и B и вычислимую функцию f,
которая на всех элементах множества A равна нулю, а на всех
элементах множества B равна 1. Поскольку наша
формальная
система " достаточно богата", в ней (для любого данного
числа n ) можно написать формулу Fn, утверждающую,
что f(n)=0. При этом для 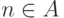 формула Fn
будет доказуемой
(протокол работы f на данном числе n, завершающийся
получением ответа 0, можно превратить в доказательство того,
что f(n)=0 ), а при
формула Fn
будет доказуемой
(протокол работы f на данном числе n, завершающийся
получением ответа 0, можно превратить в доказательство того,
что f(n)=0 ), а при 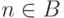 формула Fn
будет опровержимой
(поскольку можно доказать, что f(n)=1 ). Следовательно, пара
формула Fn
будет опровержимой
(поскольку можно доказать, что f(n)=1 ). Следовательно, пара 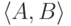 m -сводится к паре
m -сводится к паре  , и потому последняя пара
является эффективно неотделимой.
, и потому последняя пара
является эффективно неотделимой.
Еще одно любопытное утверждение, связывающее теорию алгоритмов с формальными системами, таково. Будем говорить, что две программы доказуемо различны, если можно формально доказать (скажем, в формальной арифметике), что существует вход, на котором они дают разные результаты.
Оказывается, что можно построить программу p с таким странным
свойством: никакая программа q не является доказуемо различной с p. Программу p можно было бы назвать
абсолютно
непознаваемой: ведь формально доказав любое свойство  этой программы, можно было бы доказуемо отличить p от
программы q, не обладающей этим свойством. (Мы предполагаем,
что можно предъявить некоторую программу q, про которую можно
формально доказать, что она не обладает свойством
этой программы, можно было бы доказуемо отличить p от
программы q, не обладающей этим свойством. (Мы предполагаем,
что можно предъявить некоторую программу q, про которую можно
формально доказать, что она не обладает свойством 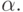 )
)
Существование непознаваемой программы p легко следует из теоремы о неподвижной точке. В самом деле, рассмотрим следующий преобразователь программ: получив на вход программу u, мы перебираем все программы v и все доказательства в формальной теории, пока не найдем некоторую программу v, доказуемо различную с u. Эта программа v и будет результатом преобразования. Если бы непознаваемой программы не существовало, то этот преобразователь был бы вычислимой функцией, не имеющей неподвижной точки.
(Конечно, это рассуждение неявно использует многочисленные свойства формальной теории, которые мы не только не доказали, но даже и не сформулировали. Например, мы неявно использовали, что доказуемо различные программы действительно различны, то есть что выводимые в нашей теории утверждения о различии программ истинны, а также многое другое.)
Можно отметить еще, что " на самом деле" наша непознаваемая программа нигде не определена, поскольку если бы она давала результат на каком-то входе, то была бы доказуемо отлична от программы, дающей другой результат на том же входе. Получается парадокс: мы вроде бы доказали, что наша функция отличается от (скажем) всюду нулевой функции, в то время как непознаваемость как раз и означает невозможность такого доказательства. Разгадка этого парадокса состоит в анализе тех самых неявно сделанных предположений (в частности, о корректности формальной системы: известная " вторая теорема Геделя" говорит, что средствами формальной системы нельзя доказать ее непротиворечивость).
Арифметическая иерархия и перемены кванторов
Мы установили, что класс арифметических множеств есть
объединение всех классов 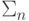 и
и 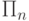 . Посмотрим
подробнее, как связан номер класса с числом перемен кванторов в
арифметической формуле.
. Посмотрим
подробнее, как связан номер класса с числом перемен кванторов в
арифметической формуле.
Чтобы сделать это, надо уточнить, какие формулы мы считаем
бескванторными. Если представлять сложение и умножение
предикатными символами, то бескванторные формулы будут
логическими комбинациями формул xi + xj = xk и xi
x xj=xk ; при этом уже для записи
формулы a+b+c=d нам понадобится квантор: она
записывается как 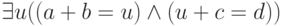 .
Мы же, как это обычно делается, будем считать сложение и умножение
функциональными символами и тем самым разрешим использовать
произвольные многочлены с целыми коэффициентами в бескванторных
формулах. При этом бескванторными формулами будут логические
комбинации выражений вида P=Q, где P
и Q произвольные
многочлены с целыми коэффициентами. Тогда верна такая теорема:
.
Мы же, как это обычно делается, будем считать сложение и умножение
функциональными символами и тем самым разрешим использовать
произвольные многочлены с целыми коэффициентами в бескванторных
формулах. При этом бескванторными формулами будут логические
комбинации выражений вида P=Q, где P
и Q произвольные
многочлены с целыми коэффициентами. Тогда верна такая теорема:
Теорема 73. Множество 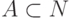 принадлежит
классу
принадлежит
классу 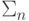 ( n >= 1 ) тогда и только тогда, когда принадлежность ему выражается
формулой в предваренной нормальной форме, начинающейся с
квантора существования и содержащей n групп одноименных
кванторов.
( n >= 1 ) тогда и только тогда, когда принадлежность ему выражается
формулой в предваренной нормальной форме, начинающейся с
квантора существования и содержащей n групп одноименных
кванторов.
(Переходя к дополнению, видим, что множество принадлежит классу 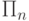 тогда и только тогда, когда принадлежность ему
выражается в предваренной нормальной форме с n группами
одноименных
кванторов, начинающейся с квантора всеобщности.)
тогда и только тогда, когда принадлежность ему
выражается в предваренной нормальной форме с n группами
одноименных
кванторов, начинающейся с квантора всеобщности.)
Мы докажем эту теорему лишь отчасти. Во-первых, если множество
задается формулой в предваренной нормальной форме с n группами
кванторов, то оно принадлежит
классу 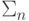 (или
(или 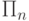 в зависимости от того,
какой
квантор первый) напомним, что k подряд идущих одноименных
кванторов можно заменить на один с помощью вычислимой биекции
между Nk и N.
в зависимости от того,
какой
квантор первый) напомним, что k подряд идущих одноименных
кванторов можно заменить на один с помощью вычислимой биекции
между Nk и N.
Более сложно доказать обратное утверждение. Основную трудность представляет случай n=1. В 1970 году Ю.В.Матиясевич, решая 10-ю проблему Гильберта, показал, что всякое перечислимое множество есть множество неотрицательных значений многочлена от нескольких переменных с целыми коэффициентами при натуральных значениях переменных. А это свойство, очевидно, записывается в виде формулы с кванторной приставкой из кванторов существования. Тем самым случай n=1 был разобран.
Если считать результат Матиясевича известным, то доказательство заканчивается, поскольку каждый следующий класс получается из предыдущего навешиванием очередного квантора.
Посмотрим, однако, что можно извлечь из приведенного нами
доказательства арифметичности вычислимых функций. Пусть дано
произвольное перечислимое множество. Его можно представить как
область определения вычислимой функции, все значения которой
равны нулю, и применить описанную нами процедуру. Тогда получится
формула, начинающаяся с кванторов существования (существуют числа,
кодирующие последовательности значений каждой переменной в смысле  -кодирования по Геделю). Затем идет квантор всеобщности
(по номеру шага работы программы: на каждом шаге переход должен
соответствовать программе). Затем идет формула, которая была
бы бескванторной, если бы не содержала в себе остатков от деления
одного выражения на другое. Но их можно устранить, добавив
еще кванторы всеобщности: утверждение типа
-кодирования по Геделю). Затем идет квантор всеобщности
(по номеру шага работы программы: на каждом шаге переход должен
соответствовать программе). Затем идет формула, которая была
бы бескванторной, если бы не содержала в себе остатков от деления
одного выражения на другое. Но их можно устранить, добавив
еще кванторы всеобщности: утверждение типа
![\forall i [\dots остаток\ от\ деления\ P\ на\ Q \dots ],](/sites/default/files/tex_cache/ca511651c58456c603767bb11493d11c.png)
где P и Q некоторые выражения, содержащие переменные (из определения \beta -кодирования) можно заменить по определению остатка на
![\forall\ i\ \forall\ u\ \forall\ v\ [(P=uQ+v) \wedge (v < Q)] \Rightarrow [\dots v \dots ].](/sites/default/files/tex_cache/e13139e30111b5ddb3752180d9b36cd6.png)
Следовательно, мы можем представить любое перечислимое множество
в виде  -формулы. Тем
самым любое множество из класса
-формулы. Тем
самым любое множество из класса 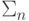 можно представить
формулой в предваренной нормальной форме
с n+1 группами кванторов, начинающейся с кванторов
существования, а любое множество из класса
можно представить
формулой в предваренной нормальной форме
с n+1 группами кванторов, начинающейся с кванторов
существования, а любое множество из класса 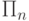 можно
представить формулой с n+1 группами кванторов, начинающейся с
квантора всеобщности.
можно
представить формулой с n+1 группами кванторов, начинающейся с
квантора всеобщности.
