m-сводимость и свойства перечислимых множеств
Изоморфизм m-полных множеств
В этом разделе мы докажем, что все m -полные множества " устроены одинаково" и отличаются друг от друга только вычислимой перестановкой.
Теорема 41.
Пусть A и B m -полные перечислимые
множества. Тогда
существует вычислимая перестановка (вычислимое взаимно
однозначное соответствие) f : N -> N, при
которой A переходит в B, то есть 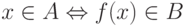 при всех x.
при всех x.
Мы будем использовать тот же прием, что и в приведенном выше доказательстве теоремы Роджерса об изоморфизме главных нумераций. Именно, мы для начала докажем такую лемму:
Лемма. Пусть A m -полное перечислимое множество. Тогда существует способ по любому натуральному числу n алгоритмически указать сколько угодно других натуральных чисел, которые принадлежат или не принадлежат A одновременно с n.
Доказательство леммы.
Как и раньше, у нас будут два способа получать новые числа,
которые ведут себя по отношению к A так же, как и исходное.
Один из них будет гарантированно давать новое число, если 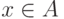 , другой если
, другой если 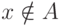 . При этом мы можем применять
оба, не зная, какой из случаев имеет место на самом деле
(и можем так этого и не узнать).
. При этом мы можем применять
оба, не зная, какой из случаев имеет место на самом деле
(и можем так этого и не узнать).
Первый способ состоит в следующем. Пусть P перечислимое неразрешимое множество. Рассмотрим перечислимое множество пар A x P. Оно сводится к A, так как A является m -полным. (Вообще-то в определении сводимости шла речь о множествах натуральных чисел, а не пар, но, как всегда, это не играет роли пары можно вычислимо нумеровать.) Другими словами, существует вычислимая всюду определенная функция f двух натуральных аргументов с таким свойством:
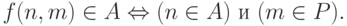
В частности, при 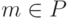 числа n
и f(n,m) одновременно
принадлежат или не принадлежат A. Поэтому,
расположив P
в вычислимую последовательность p(0),p(1), ..., мы можем
вычислять числа f(n,p(0)),f(n,p(1)), ... и получать новые
числа, которые принадлежат или не принадлежат A одновременно
с n.
числа n
и f(n,m) одновременно
принадлежат или не принадлежат A. Поэтому,
расположив P
в вычислимую последовательность p(0),p(1), ..., мы можем
вычислять числа f(n,p(0)),f(n,p(1)), ... и получать новые
числа, которые принадлежат или не принадлежат A одновременно
с n.
Пусть 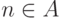 . Покажем, что множество X
получаемых таким
образом чисел (все они в этом случае тоже принадлежат A ) будет
бесконечно. В самом деле,
. Покажем, что множество X
получаемых таким
образом чисел (все они в этом случае тоже принадлежат A ) будет
бесконечно. В самом деле, 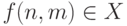 при
при 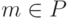 (по
построению X ) и
(по
построению X ) и 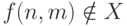 при
при 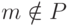 (поскольку в
этом случае
(поскольку в
этом случае 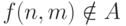 , а
, а 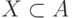 ).
Таким образом, функция m -> f(n,m) сводит неразрешимое
множество P к множеству X, так что X
неразрешимо и потому
бесконечно.
).
Таким образом, функция m -> f(n,m) сводит неразрешимое
множество P к множеству X, так что X
неразрешимо и потому
бесконечно.
Теперь опишем другой способ, который гарантирует успех,
если 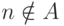 . Возьмем два перечислимых неотделимых
множества P
и Q. Рассмотрим перечислимое множество пар
. Возьмем два перечислимых неотделимых
множества P
и Q. Рассмотрим перечислимое множество пар 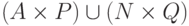 . Пусть функция f сводит его
к A.
Это означает, что
. Пусть функция f сводит его
к A.
Это означает, что 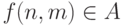 тогда и только тогда, когда
тогда и только тогда, когда 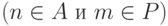 или
или 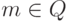 .
Как и
прежде, при
.
Как и
прежде, при 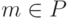 числа n и f(n,m)
одновременно
принадлежат или не принадлежат A, так что мы можем снова
рассмотреть последовательность f(n,p(0)),f(n,p(1)),...;
осталось лишь показать, что (если
числа n и f(n,m)
одновременно
принадлежат или не принадлежат A, так что мы можем снова
рассмотреть последовательность f(n,p(0)),f(n,p(1)),...;
осталось лишь показать, что (если 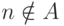 ) в этой
последовательности бесконечно много различных членов.
) в этой
последовательности бесконечно много различных членов.
Пусть это не так и множество X всех членов этой
последовательности конечно. По нашему предположению X не
пересекается с A. Заметим, что 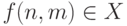 при
при 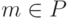 (по
построению) и
(по
построению) и 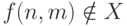 при
при 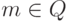 (так
как в этом
случае
(так
как в этом
случае 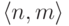 принадлежит нашему перечислимому
множеству пар и f(n,m) принадлежит A ). Таким образом,
прообраз множества X при отображении m -> f(n,m)
отделяет P от Q. Но этот прообраз разрешим
( X разрешимо,
ибо конечно, а указанное отображение всюду определено и
вычислимо). А по нашему предположению множества P
и Q нельзя
отделить разрешимым множеством.
принадлежит нашему перечислимому
множеству пар и f(n,m) принадлежит A ). Таким образом,
прообраз множества X при отображении m -> f(n,m)
отделяет P от Q. Но этот прообраз разрешим
( X разрешимо,
ибо конечно, а указанное отображение всюду определено и
вычислимо). А по нашему предположению множества P
и Q нельзя
отделить разрешимым множеством.
Итак, мы привели два способа получать новые элементы, которые принадлежат или не принадлежат A одновременно с исходным. Применяя их параллельно, мы наверняка добьемся результата. Лемма доказана.
Пусть теперь A и B два m -полных перечислимых множества. Докажем, что они отличаются лишь вычислимой перестановкой натурального ряда. Будем строить эту перестановку по шагам. На k -ом шаге мы имеем взаимно однозначное соответствие
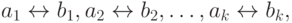
при котором  при всех i. На четных
шагах мы
берем минимальное число, не входящее в левую часть этого
соответствия. Используя факт m -сводимости A
к B, мы
находим ему компаньона. При этом доказанная нами лемма позволяет
выбрать компаньона, не встречающегося среди уже имеющихся
справа элементов. На нечетных шагах мы делаем то же самое,
только справа налево.
при всех i. На четных
шагах мы
берем минимальное число, не входящее в левую часть этого
соответствия. Используя факт m -сводимости A
к B, мы
находим ему компаньона. При этом доказанная нами лемма позволяет
выбрать компаньона, не встречающегося среди уже имеющихся
справа элементов. На нечетных шагах мы делаем то же самое,
только справа налево.
В пределе этот процесс дает искомую вычислимую перестановку, связывающую A и B.
С точки зрения теории алгоритмов два множества, отличающиеся лишь вычислимой перестановкой, обладают одинаковыми свойствами. Поэтому доказанная теорема показывает, что по существу имеется лишь одно m -полное перечислимое множество (или, что то же, лишь одно перечислимое множество с эффективно неперечислимым дополнением).
Продуктивные множества
В этом разделе мы используем теорему о неподвижной точке для получения такого (неожиданного на первый взгляд) результата: определение эффективной неперечислимости множества A не изменится, если мы ограничимся лишь (перечислимыми) подмножествами множества A.
Зафиксируем некоторую главную нумерацию перечислимых множеств (множество с номером n мы обозначаем Wn ). Говорят, что множество A является продуктивным, если существует вычислимая (не обязательно всюду определенная) функция f с таким свойством: она применима к любому номеру n любого подмножества Wn множества A и дает элемент в их разности:
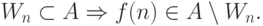
49. Докажите, что продуктивное множество не может быть иммунным.
Ясно, что требования в определении продуктивности лишь часть требований из определения эффективно неперечислимого множества, так что любое эффективно неперечислимое множество продуктивно. Удивительным образом оказывается, что верно и обратное.
Теорема 42. Пусть A продуктивное множество, K произвольное перечислимое множество. Тогда дополнение к K m -сводится к A.
(Из этого следует, что A является эффективно неперечислимым, см. выше.)
Пусть f функция, которая существует по определению продуктивности (и дает элемент вне подмножества с указанным номером).
Мы построим всюду определенную вычислимую функцию s с такими свойствами:
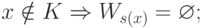
-
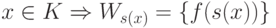 .
.
(второе свойство подразумевает, что f(s(x)) определено при 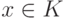 ).
Прежде чем делать это с помощью теоремы о неподвижной точке,
заметим, что в первом случае f(s(x)) определено и
принадлежит A:
поскольку множество
с номером s(x) пусто и является подмножеством A,
число f(s(x)) должно быть элементом A. Напротив, во
втором случае f(s(x)) не принадлежит A. В самом деле, если бы это
было не
так, то множество Ws(x) было бы подмножеством A,
и потому
число f(s(x)) должно было бы быть элементом A, не
входящим в
это подмножество а оно входит.
).
Прежде чем делать это с помощью теоремы о неподвижной точке,
заметим, что в первом случае f(s(x)) определено и
принадлежит A:
поскольку множество
с номером s(x) пусто и является подмножеством A,
число f(s(x)) должно быть элементом A. Напротив, во
втором случае f(s(x)) не принадлежит A. В самом деле, если бы это
было не
так, то множество Ws(x) было бы подмножеством A,
и потому
число f(s(x)) должно было бы быть элементом A, не
входящим в
это подмножество а оно входит.
Поэтому если нам удастся построить такую функцию s, то функция x -> f(s(x)) будет m -сводить дополнение множества K к множеству A, как мы и обещали. Как же ее строить?
Если бы во втором свойстве (для 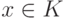 ) стояло
не f(s(x)),
а, скажем, просто f(x), никакой проблемы бы не было. Как обычно,
мы рассмотрели бы перечислимое множество пар
) стояло
не f(s(x)),
а, скажем, просто f(x), никакой проблемы бы не было. Как обычно,
мы рассмотрели бы перечислимое множество пар

сечения этого множества имели бы требуемый вид и осталось бы только воспользоваться тем, что нумерация главная. Но в нашем случае, когда в правой части второго свойства стоит f(s(x)), так просто поступить нельзя: как в истории о курице и яйце, для построения V нам надо иметь s(x), а для построения s(x) надо иметь V.
Именно такого рода трудности позволяет преодолевать теорема о неподвижной точке. Построим всюду определенную вычислимую функцию двух аргументов h с такими свойствами:
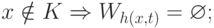
-
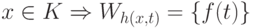 .
.
(Подобные вещи мы делали многократно последний раз в предыдущем
абзаце. Отметим, что f(t) может быть и не определено, тогда
под {f(t)}
мы понимаем пустое множество.) По теореме о неподвижной точке (для
перечислимых множеств)
при каждом x функция 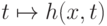 имеет
неподвижную точку,
и, как мы говорили в разделе о неподвижной точке с параметром,
эту неподвижную точку можно выбрать вычислимо зависящей от x.
Таким образом, существует всюду определенная вычислимая функция s,
для которой
имеет
неподвижную точку,
и, как мы говорили в разделе о неподвижной точке с параметром,
эту неподвижную точку можно выбрать вычислимо зависящей от x.
Таким образом, существует всюду определенная вычислимая функция s,
для которой
Ws(x)=Wh(x,s(x))
при всех x. Это равенство можно продолжить:
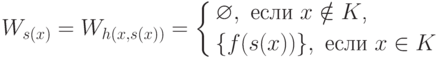
- это ровно то, чего мы и хотели. Заметим, что значение f(s(x)) определено
при всех x (иначе 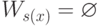 , и f(s(x)) должно
быть определено). Тем самым, теорема о неподвижной
точке позволяет отыскать взаимно согласованные яйцо и курицу и
завершает доказательство.
, и f(s(x)) должно
быть определено). Тем самым, теорема о неподвижной
точке позволяет отыскать взаимно согласованные яйцо и курицу и
завершает доказательство.
