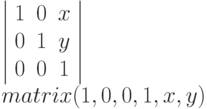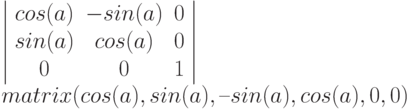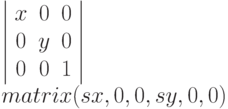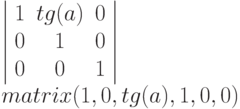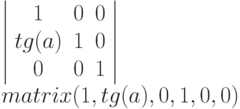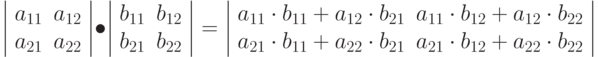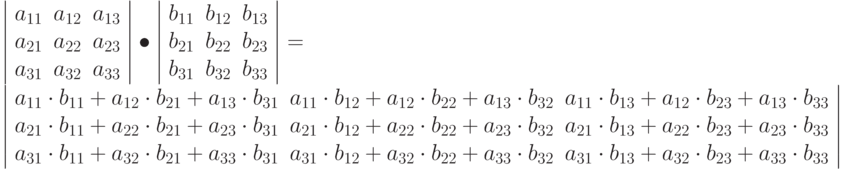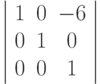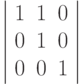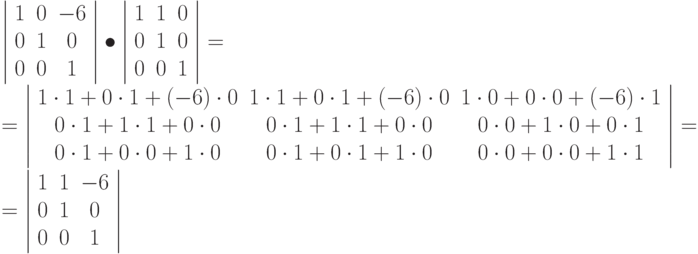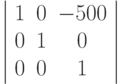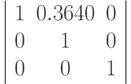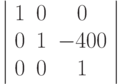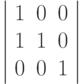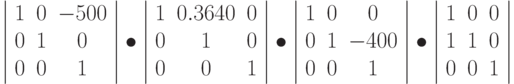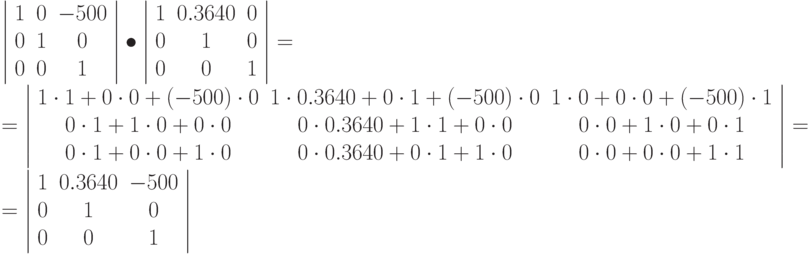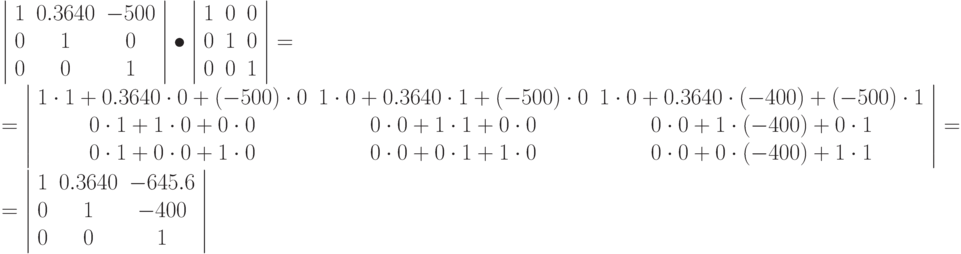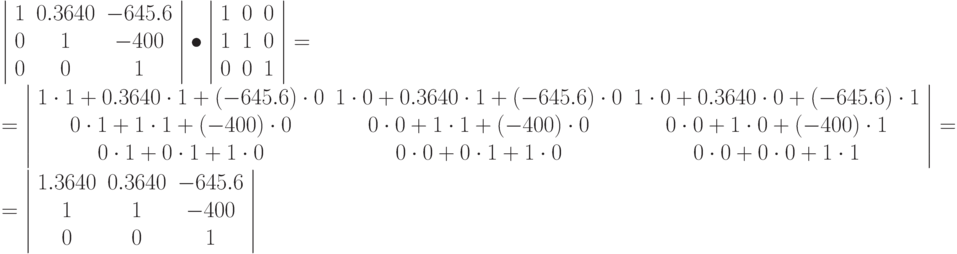Matrix
Трансформация matrix представляет собой способ компактной записи серии преобразований. Графически эта команда не содержит собственных изменений объекта. Она лишь выражает применение одной или нескольких команд типа translation, rotate, scale, skewX и skewY. Математически1, все преобразования могут быть выражены в виде матрицы третьего порядка следующим образом:
Команда будет выглядеть так:
Каждое из преобразований представляется своей матрицей и соответствующей командой matrix.
Команда translation:
Команда rotate:
Команда scale:
Команда skewX:
Команда skewY:
Практически, для перехода к новой форме записи нужно просто взять исходные параметры команды и аккуратно их подставить в нужные позиции. Для команд rotate, skewX и skewY дополнительно следует вычислить тригонометрические функции углов. В табл. 6.6 приводятся примеры использования этой записи.
Таблица
6.6.
Команда matrix.
| № |
Код |
Вид в браузере |
| 6.6.1 |
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="200" height="150"
xmlns="http://www.w3.org/2000/svg" version="1.1">
<title> Лекция 6. Трансформации </title>
<desc>
Пример matrix1.svg ( translate1.svg)
</desc>
<rect x="25" y="25" width="50" height="25"
fill="skyblue" stroke="red" stroke-width="2"/>
<rect x="25" y="25" width="50" height="25"
fill="palegreen" stroke="red" stroke-width="2"
transform="matrix(1, 0, 0, 1, 100,75)"/>
<!-- transform="translate(100,75)-->
</svg>
Листинг
6.6.1.
Пример matrix1.svg ( translate1.svg)
|
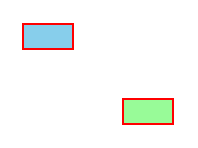 |
| Описание |
|---|
| Запись команды translate в форме matrix. |
| № |
Код |
Вид в браузере |
| 6.6.2 |
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="200" height="100"
xmlns="http://www.w3.org/2000/svg" version="1.1">
<title> Лекция 6. Трансформации </title>
<desc>
Пример matrix2.svg (scale2.svg)
</desc>
<rect x="25" y="25" width="50" height="25"
fill="skyblue" stroke="red" stroke-width="2"/>
<rect x="25" y="50" width="50" height="25"
fill="palegreen" stroke="red" stroke-width="2"
transform="matrix(2, 0, 0, 1, 0, 0)"/>
<!-- transform="scale(2,1)"-->
</svg>
Листинг
6.6.2.
Пример matrix2.svg (scale2.svg)
|
 |
| Описание |
|---|
| Запись команды scale в форме matrix. |
| № |
Код |
Вид в браузере |
| 6.6.3 |
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="210" height="210"
xmlns="http://www.w3.org/2000/svg" version="1.1">
<title> Лекция 6. Трансформации </title>
<desc>
Пример matrix3.svg (rotate1.svg)
</desc>
<!--Исходная фигура-->
<g>
<rect x="105" y="4" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="105" y="4" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
</g>
<!--Повернутая фигура-->
<g transform="matrix(0.7071, 0.7071, -0.7071, 0.7071, 0, 0)" >
<rect x="105" y="4" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="105" y="4" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
<!-- transform="rotate(45)"-->
</g>
</svg>
Листинг
6.6.3.
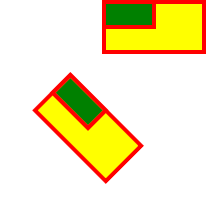
Пример matrix3.svg (rotate1.svg)
|
 |
| Описание |
|---|
| Запись команды rotate в форме matrix. |
| № |
Код |
Вид в браузере |
| 6.6.4 |
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="200" height="200"
xmlns="http://www.w3.org/2000/svg" version="1.1">
<title> Лекция 6. Трансформации </title>
<desc>
Пример matrix4.svg (skew1.svg)
</desc>
<!--Исходная фигура-->
<g>
<rect x="10" y="10" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="10" y="10" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
</g>
<!--Трансформированная фигура -->
<g transform="matrix(1, 0, 1, 1, 0, 0)" >
<rect x="10" y="10" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="10" y="10" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
<!-- transform="skewX(45)"-->
</g>
</svg>
Листинг
6.6.4.
Пример matrix4.svg (skew1.svg)
|
 |
| Описание |
|---|
| Запись команды skewX в форме matrix. tg(45)=1
|
| № |
Код |
Вид в браузере |
| 6.6.5 |
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="200" height="200"
xmlns="http://www.w3.org/2000/svg" version="1.1">
<title> Лекция 6. Трансформации </title>
<desc>
Пример matrix5.svg (skew5.svg)
</desc>
<!--Исходная фигура-->
<g>
<rect x="10" y="10" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="10" y="10" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
</g>
<!--Трансформированная фигура -->
<g transform="matrix(1, 1, 0, 1, 0, 0)" >
<rect x="10" y="10" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="10" y="10" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
<!-- transform="skewY(45)"-->
</g>
</svg>
Листинг
6.6.5.
Пример matrix5.svg (skew5.svg)
|
 |
| Описание |
|---|
| Запись команды skewY в форме matrix. tg(45)=1
|
Мы разобрали запись в виде матрицы отдельных команд. Немного более сложно обстоят дела с записью нескольких команд, например, translate и skew в виде одной матрицы. Результирующая матрица представляет собой произведение отдельных матриц. Рассмотрим для начала произведение матриц, содержащих по две строки и два столбца:
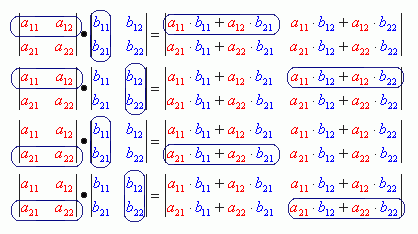
Обратите внимание на индексы – индекс 12, к примеру, означает, что элемент b12 находится в первой строке и втором столбце. Результирующая матрица получается сложением и умножением отдельных элементов по следующей схеме (рис. 6.8):
Рис.
6.8.
Умножение матриц второго порядка
Аналогичным образом осуществляется умножение матриц третьего порядка:
Для отдельного элемента результирующей матрицы, находящегося во второй строке первого столбца можно выделить схему (рис. 6.9):
Рис.
6.9.
Умножение матриц третьего порядка
Итак, для получения результирующей матрицы нескольких команд нужно записать отдельные матрицы, а затем их перемножить. В табл. 6.7 приведены примеры подобных матриц.
Таблица
6.7.
Команда matrix для нескольких преобразований.
| № |
Код |
Вид в браузере |
| 6.7.1 |
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="200" height="200"
xmlns="http://www.w3.org/2000/svg" version="1.1">
<title> Лекция 6. Трансформации </title>
<desc>
Пример matrixGroup1.svg (skew2.svg)
</desc>
<!--Исходная фигура-->
<g>
<rect x="10" y="10" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="10" y="10" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
</g>
<!--Трансформированная фигура -->
<g transform="matrix(1, 0, 1, 1, -6, 0)" >
<rect x="10" y="10" width="100" height="50"
fill="yellow" stroke="red" stroke-width="4"/>
<rect x="10" y="10" width="50" height="25"
fill="green" stroke="red" stroke-width="4"/>
</g>
<!-- transform="translate(-6,0) skewX(45)"-->
</svg>
Листинг
6.7.1.
Пример matrixGroup1.svg (skew2.svg)
|
 |
| Описание |
|---|
Преобразование состоит из двух команд. Запишем их отдельные матрицы:
-
translate(-6,0):
-
skewX(45):
Вычисляем произведение матриц:
tg(45)=1
Результирующая команда: matrix(1,0,1,1,-6,0)
|
| № |
Код |
Вид в браузере |
| 6.7.2 |
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN"
"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="200" height="100"
xmlns="http://www.w3.org/2000/svg" version="1.1"
viewBox="0 0 1000 950">
<title> Лекция 6. Трансформации </title>
<desc>
Пример matrixGroup2.svg (skew7.svg)
</desc>
<circle cx="500" cy="400" r="300"
fill="lightskyblue"
stroke="blue" stroke-width="30"/>
<ellipse cx="500" cy="500" rx="150" ry="100"
fill="none"
stroke="blue" stroke-width="30"/>
<rect x="300" y="370" width="400" height="130"
fill="lightskyblue"/>
<ellipse cx="350" cy="300" rx="100" ry="50"
fill="white" stroke="blue" stroke-width="30"/>
<ellipse cx="650" cy="300" rx="100" ry="50"
fill="white" stroke="blue" stroke-width="30"/>
<circle cx="350" cy="300" r="25"
fill="black"/>
<circle cx="650" cy="300" r="25"
fill="black"/>
<g transform="matrix(1.3640, 1, 0.3640, 1, -645.6, -400)">
<!-- transform="translate(-500,0) skewX(20)
translate(0, -400) skewY(45)"-->
<circle cx="500" cy="400" r="300"
fill="lightskyblue" stroke="blue" stroke-width="30"/>
<ellipse cx="500" cy="500" rx="150" ry="100"
fill="none" stroke="blue" stroke-width="30"/>
<rect x="300" y="370" width="400" height="130"
fill="lightskyblue"/>
<ellipse cx="350" cy="300" rx="100" ry="50"
fill="white" stroke="blue" stroke-width="30"/>
<ellipse cx="650" cy="300" rx="100" ry="50"
fill="white" stroke="blue" stroke-width="30"/>
<circle cx="350" cy="300" r="25"
fill="black"/>
<circle cx="650" cy="300" r="25"
fill="black"/>
</g>
</svg>
Листинг
6.7.2.
Пример matrixGroup2.svg (skew7.svg)
|
 |
| Описание |
|---|
Преобразование состоит из четырех команд. Запишем их отдельные матрицы:
-
translate(-500, 0):
-
skewX(20):
-
translate(0, -400):
-
skewY(45):
Результирующая матрица будет представлять собой произведение четырех матриц:
Вычисляем произведение первых двух матриц:
Умножаем результат на третью матрицу:
Наконец, результат умножаем на четвертую матрицу:
tg(45)=1, tg(20) = 0.3640
Результирующая команда: matrix(1.3640,1,0.3640,1,-645.6,-400)
|
Запись серии команд в виде матрицы позволяет сократить запись и, следовательно, уменьшить размер SVG – документа.
Вычисление матриц в программе Mathcad
Основная сложность применения команды matrix – это вычисление произведения матриц, представляющее собой довольно трудоемкую и кропотливую задачу. Пакет Mathcad
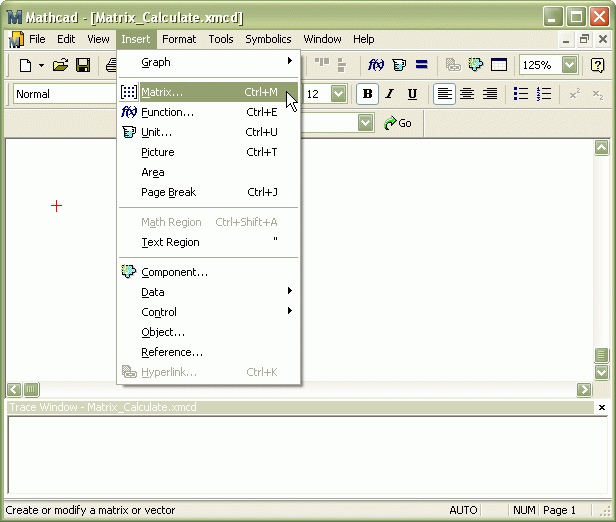
(http://www.ptc.com/go/mathsoft) – мощное средство для решения широкого класса вычислительных задач, содержит удобные инструменты для работы с матрицами. После установки и запуска программы можно сразу приступать к вычислениям. В главном меню выбираем "Insert – Matrix" ( или нажимаем Ctrl+M) (рис. 6.10):
Рис.
6.10.
Вставка матрицы
В появившемся диалоговом окне выбираем матрицы размером 3х3 (рис. 6.11):
Рис.
6.11.
Определение размера матрицы
В документе появляется шаблон, в который можно вводить числа (рис. 6.12):
Рис.
6.12.
Шаблон матрицы
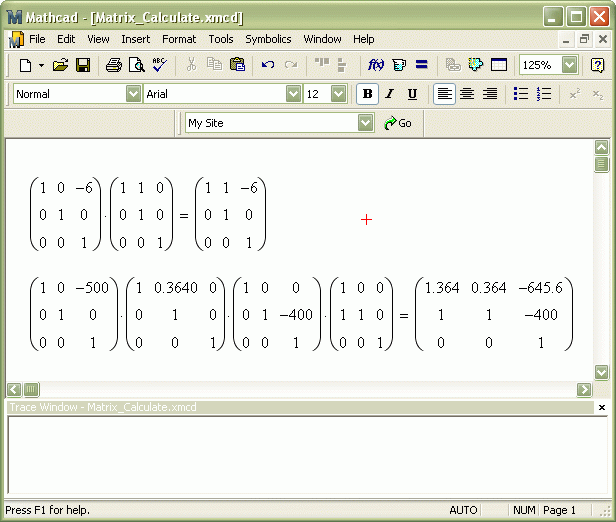
После завершения ввода вводим знак равенства "=" и программа автоматически отображает результирующую матрицу (рис. 6.13):
Рис.
6.13.
Готовые матрицы
Программа поддерживает также вычисление тригонометрических функций, которые можно задавать непосредственно в текстовом виде.