Машинное обучение

3. Обзор возможностей библиотеки OpenCV для решения задач обучения без учителя

3.1. Задача кластеризации

Задача кластеризации заключается в разбиении выборки на непересекающиеся подмножества таким образом, чтобы схожие точки (обычно близкие в некоторой метрике) попали в одно подмножество (кластер), а точки из разных кластеров сильно друг от друга отличались (были далеки). Для решения данной задачи в библиотеки OpenCV реализован метод центров тяжести (k-means) и EM-алгоритм. В данной лабораторной работе рассматривается использование программной реализации метод центров тяжести, как одного из наиболее популярных алгоритмов кластеризации на настоящий момент.

3.2. Метод центров тяжести (k-means)

Метод центров тяжести разбивает выборку на заданное количество кластеров K путем выбора их центров. Поиск центров кластеров производится из соображений минимизации суммарного расстояния от каждой точки до ближайшего центра с помощью метода локальной оптимизации. Так как алгоритм не гарантирует достижения глобального минимума, ключевую роль играет начальная инициализация центров кластеров. Распространенным методом является случайный (с равной вероятностью) выбор K точек из имеющегося множества . Однако алгоритм центров тяжести, запущенный на таких начальных данных может выдать в результате локальный минимум сколь угодно хуже глобального. Альтернативой является метод k-means++ [5], предложенный Д. Артуром и С. Вассильвицким, основанный на последовательном выборе K точек из выборки случайным образом, но с вероятностью пропорциональной квадрату расстояния от точки до ближайшего уже выбранного центра. В данном случае, математическое ожидание отношения найденного минимума к глобальному является величиной .

Метод центров тяжести с евклидовой метрикой реализован в библиотеке OpenCV в виде функции kmeans модуля core:

double kmeans( InputArray data, 
               int K, 
               InputOutputArray bestLabels, 
               TermCriteria criteria, 
               int attempts, 
               int flags, 
               OutputArray centers=noArray() ); 
               

Рассмотрим параметры данной функции:

• data – матрица типа CV_32F, в которой каждой строке соответствует точка выборки.
• K – количество кластеров, получаемых на выходе алгоритма.
• bestLabels – матрица размера 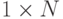, в которую для каждой точки 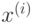будет сохранен номер кластера, в который попала данная точка.
• criteria – критерий останова итерационного метода оптимизации. Алгоритм k-means может закончить работу либо после совершения заданного количества итераций, либо если каждый центр кластера сдвинется на величину меньше criteria.epsilon.
• attempts – количество запусков алгоритма k-means с различными начальными центрами кластеров. В качестве конечного разбиения будет возвращен наилучший из полученных результатов.
• flags – метод генерации центров кластеров перед запуском алгоритма k-means. Допустимые значения: KMEANS_RANDOM_CENTERS – случайный равновероятный выбор центров, KMEANS_PP_CENTERS – случайный выбор методом k- means++, KMEANS_USE_INITIAL_LABELS – для первого запуска используется заданное с помощью параметра bestLabels разбиение.
• centers – матрица с наилучшими найденными центрами кластеров. Каждая строка соответствует координатам центра одно кластера.

Данная функция возвращает сумму квадратов расстояний от каждой точки до ближайшего к ней центра.

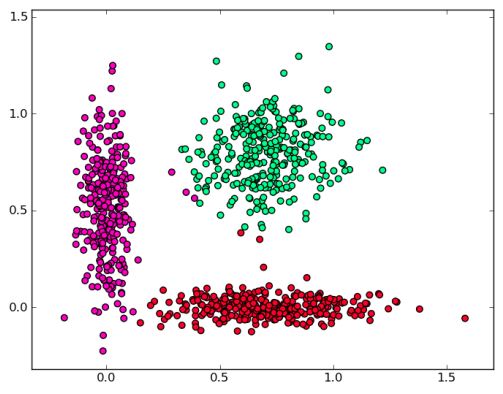
Рассмотрим пример использования функции kmeans для кластеризации точек на плоскости. Результат полученной кластеризации приведен на рис. 10.5.

#include <opencv2/core/core.hpp> 
 
using namespace cv; 
 
Mat generateDataset() 
{ 
    int n = 300; 
    Mat data(3 * n, 2, CV_32F); 
     
    randn(data(Range(0, n), Range(0, 1)), 0.0, 0.05); 
    randn(data(Range(0, n), Range(1, 2)), 0.5, 0.25); 
 
    randn(data(Range(n, 2 * n), Range(0, 1)), 0.7, 0.25); 
    randn(data(Range(n, 2 * n), Range(1, 2)), 0.0, 0.05); 
 
    randn(data(Range(2 * n, 3 * n), Range(0, 1)), 
          0.7, 0.15); 
    randn(data(Range(2 * n, 3 * n), Range(1, 2)), 
          0.8, 0.15); 
     
    return data; 
} 
 
int main(int argc, char* argv[]) 
{ 
    Mat samples = generateDataset(); 
 
    Mat labels; 
    Mat centers; 
    kmeans(samples, 
        3, 
        labels, 
        TermCriteria(TermCriteria::COUNT + 
                     TermCriteria::EPS, 10000, 0.001),         10, 
        KMEANS_PP_CENTERS, 
        centers); 
     
    return 0; 
} 

Рис. 10.5. Кластеризация методом центров тяжести (k-means)

4. Программная реализация

4.1. Разработка приложения для решения задач классификации

4.1.1. Требования к приложению

В рамках данной лабораторной работы предлагается разработать приложение для решения задач классификации, предусматривающее возможность применения рассмотренных выше алгоритмов машинного обучения. К приложению предъявляются следующие требования:

1. Организация диалога с пользователем для загрузки набора данных из файла с последующим выбором алгоритма обучения с учителем и его параметров.
2. Обучение модели на загруженных данных.
3. Вычисление ошибки классификации на обучающей и тестовой выборках.
4. Визуализация результата работы алгоритмов в случае двумерного пространства признаков.

4.1.2. Структура приложения

Приложение будет состоять из набора модулей (cvsvm.cpp/h, cvdtree.cpp/h, cvrtrees.cpp/h, cvgbtrees.cpp/h), каждый из которых предназначен для работы (запрос у пользователя параметров, обучение и предсказание) рассматриваемых алгоритмов обучения, модуля вычисления ошибки классификации (errorMetrics.cpp/h), модуля визуализации данных (drawingFunctions.cpp/h) и основного модуля (main.cpp), содержащего общую логику работы программы. Основной модуль и модуль визуализации предоставляются в реализованном виде, следовательно, необходимо реализовать непосредственно работу с различными алгоритмами обучения с учителем. Далее рассматриваются интерфейсы готовых функций, а также функционал, который предлагается реализовать самостоятельно.

Модуль визуализации данных содержит функцию рисования точек из двумерного пространства признаков drawPoints:

void drawPoints(Mat & img, 
                const Mat & data, 
                const Mat & classes, 
                const Mat & ranges, 
                std::map<int, Scalar> & classColors, 
                int drawingMode = 0); 
                

В качестве аргументов данная функция принимает:

1. img – изображение (матрица типа CV_8UC3).
2. data – матрица типа CV_32F, содержащая признаковые описания объектов выборки.
3. classes – матрица типа CV_32S с номерами классов объектов выборки.
4. ranges – матрица типа CV_64F, содержащая в первом столбце визуализируемый диапазон первого признака (отображаемого по оси X), а вот втором – второго.
5. classColors – соответствие номеров классов и цветов точек. Если какому-либо классу не будет поставлен в соответствие цвет, то он будет сгенерирован случайным образом.
6. drawingMode – тип отображаемых точек. Для рисования закрашенных точек используется drawingMode=0, для "выколотых" точек drawingMode=1, для рисования черных точек drawingMode=2. Использование данного параметра позволяет различным образом отображать точки обучающей и тестовой выборок, а также (при использовании SVM) опорных векторов.

Функция drawPartition позволяет отображать разбиение пространства признаков на области, соответствующие разным классам, путем вычисления предсказаний на равномерной сетке:

void drawPartition(Mat & img, 
                   map<int, Scalar> & classColors, 
                   const Mat & dataRanges, 
                   const Size stepsNum, 
                   const CvStatModel & model, 
                   getPredictedClassLabel * predictLabel); 
                   

Параметры функции:

• img – изображение (матрица типа CV_8UC3).
• classColors – соответствие номеров классов и цветов точек. Если какому-либо классу не будет поставлен в соответствие цвет, то он будет сгенерирован случайным образом.
• dataRanges – матрица типа CV_64F, содержащая в первом столбце визуализируемый диапазон первого признака (отображаемого по оси X ), а вот втором – второго.
• stepsNum – количество узлов сетки в каждом из направлений.
• model – обученная модель для выполнения предсказаний в узлах сетки.
• predictLabel – указатель на функцию вычисления пресказаний с помощью model.

Функция getRanges предназначена для поиска матрицы минимальных и максимальных значений каждого признака в выборке data:

 
Mat getRanges(const Mat & data); 

Функция readDatasetFromFile позволяет считать данные (обучающую и тестовую выборки) из XML- или YAML-файла.

 
void readDatasetFromFile(Mat & featuresTrain, 
                         Mat & classesTrain, 
                         Mat & featuresTest, 
                         Mat & classesTest); 
                         

Файл должен содержать матрицы признаков объектов обучающей ("featuresTrain") и тестовой ("featuresTest") выборок и соответствующих им классов ("classesTrain" и "classesTest") в формате OpenCV. Матрицы classesTrain и classesTest должны иметь тип CV_32S, featuresTrain и featuresTest – CV_32F.

Основная логика программы сосредоточена в модуле main.cpp и выглядит следующим образом:

• В цикле пользователю предлагается загрузить данные из файла, либо применить к уже загруженным данным алгоритм обучения с учителем из списка: машина опорных векторов, дерево решений, случайный лес, градиентный бустинг деревьев решений.
• Если выбран алгоритм решения задачи классификации, у пользователя запрашиваются параметры алгоритма обучения, производится обучение и вычисление ошибок на обучающей и тестовой выборках. Если размерность пространства признаков равна двум, то данные и разбиение пространства признаков полученной моделью отображаются в новом графическом окне.
• Графические окна не обязательно закрывать перед применением другого алгоритма к тем же данным, что позволяет сравнить результаты работы различных методов. Однако при загрузке новых данных все графические окна будут закрыты автоматически.

Перейдем к рассмотрению функций, которые предлагается реализовать самостоятельно. Прежде всего, это функции, запускающие обучение моделей:

void trainSVM(const Mat & trainSamples, 
              const Mat & trainClasses, 
              const CvSVMParams & params, 
              CvSVM & svm); 
void trainDTree(const Mat & trainSamples, 
                const Mat & trainClasses, 
                const CvDTreeParams & params, 
                CvDTree & dtree); 
void trainRTrees(const Mat & trainSamples, 
                 const Mat & trainClasses, 
                 const CvRTParams & params, 
                 CvRTrees & rtrees); 
void trainGBTrees(const Mat & trainSamples, 
                  const Mat & trainClasses, 
                  const CvGBTreesParams & params, 
                  CvGBTrees & gbtrees); 
                  

Данные функции находятся в файлах cvsvm.cpp, cvdtree.cpp, cvrtrees.cpp, cvgbtrees.cpp соответственно. В теле каждой функции требуется вызвать метод переданного в нее объекта для обучения модели на данных trainSamples (матрица признаковых описаний объектов) и trainClasses (матрица номеров классов) с параметрами params. Также требуется реализация функций для предсказания:

int getSVMPrediction(const Mat & sample, 
                     const CvStatModel & model); 
int getDTreePrediction(const Mat & sample, 
                       const CvStatModel & model); 
int getRTreesPrediction(const Mat & sample, 
                        const CvStatModel & model); 
int getGBTreesPrediction(const Mat & sample, 
                         const CvStatModel & model); 
                         

Функции, принимают признаковое описание объекта sample и обученную модель model, возвращая номер предсказанного класса. Интерфейс данных функций унифицирован для более простого подсчета ошибок на обучающей и тестовой выборках. Функции принимают объекты базового типа CvStatModel, однако, фактичеси это должны быть объекты соответствующих классов: для getSVMPrediction объект класса CvSVM, для getDTreePrediction – CvDTree и т.д.

Также предлагается реализовать функцию getSupportVectors (файл cvsvm.cpp), принимающую обученную машину опорных векторов svm и возвращающую матрицу, где каждая строка соответствует опорному вектору:

Mat getSupportVectors(const CvSVM & svm); 

Функции запроса параметров каждого из рассматриваемых алгоритмов обучения предоставляются в готовом виде и рекомендуются для самостоятельного разбора.

Также в рамках лабораторной работы предлагается реализовать функцию вычисления ошибки классификации (долю неправильно классифицированных объектов выборки) getClassificationError:

float getClassificationError(const Mat & samples, 
      const Mat & classes, 
      const CvStatModel & model, 
      int (*predict) (const Mat & sample, 
                      const CvStatModel & model)); 
                      

Параметры функции:

• samples – признаковые описания объектов выборки.
• classes – номера классов (истинные значения целевого признака) для объектов выборки.
• model – обученная модель.
• predict – указатель на функцию, принимающую один объект выборки и модель и возвращающую номер предсказанного класса.

Данная функция должна вычислять доля неправильно классифицированных объектов выборки.

После того, как описанные функции будут реализованы, предлагается применить рассмотренные алгоритмы классификации к наборам данных из файлов dataset1.yml, dataset2.yml, dataset3.yml, dataset4.yml, datasetMulticlass.yml и datasetHighDim.yml. А также проанализировать, на каких данных лучше/хуже работает тот или иной подход и какое влияние на конечную модель оказывают параметры алгоритма обучения.