|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Машинное обучение
2.5. Градиентный бустинг деревьев решений
Градиентный бустинг, как и любой бустинг алгоритм, последовательно
строит базовые модели так, что каждая следующая улучшает качество
всего ансамбля. Градиентный бустинг деревьев решений строит модель в
виде суммы деревьев
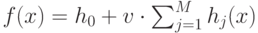 , где
, где 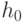 – некоторая константная модель
(начальное приближение),
– некоторая константная модель
(начальное приближение), ![v \in (0,1]](/sites/default/files/tex_cache/1c4535deafd10052f9cbc0b677dfb38a.png) – параметр, регулирующий скорость
обучения и влияние отдельных деревьев на всю модель,
– параметр, регулирующий скорость
обучения и влияние отдельных деревьев на всю модель, 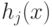 –
регрессионные деревья решений. Новые слагаемые-деревья добавляются в
сумму путем жадной минимизации эмпирического риска, заданного
некоторой функцией потерь
–
регрессионные деревья решений. Новые слагаемые-деревья добавляются в
сумму путем жадной минимизации эмпирического риска, заданного
некоторой функцией потерь 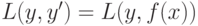 . Данный метод без
серьезной модификации может применяться для любой
дифференцируемой функции потерь.
. Данный метод без
серьезной модификации может применяться для любой
дифференцируемой функции потерь.
Метод градиентного бустинга деревьев решений в библиотеке OpenCV реализован в виде класса CvGBTrees. Для запуска обучения модели реализован метод train:
bool train( const Mat< trainData,
int tflag,
const Mat< responses,
const Mat< varIdx=Mat(),
const Mat< sampleIdx=Mat(),
const Mat< varType=Mat(), const Mat< missingDataMask=Mat(),
CvGBTreesParams params=CvGBTreesParams(),
bool update=false );
Использование данного метода аналогично рассмотренным ранее алгоритмам за исключением следующих моментов: параметр update на настоящий момент является фиктивным, не поддерживается задание используемых прецедентов с помощью маски, по умолчанию обучается регрессионная модель (для обучения классификатора необходимо явно задать категориальный тип целевого признака и выбрать соответствующую функцию потерь). Параметры алгоритма обучения модели градиентного бустинга деревьев решений представляются структурой CvGBTreesParams:
struct CvGBTreesParams : public CvDTreeParams
{
int weak_count;
int loss_function_type;
float subsample_portion;
float shrinkage;
CvGBTreesParams();
CvGBTreesParams( int loss_function_type,
int weak_count,
float shrinkage,
float subsample_portion,
int max_depth,
bool use_surrogates );
};
Рассмотрим значения ее полей:
-
loss_function_type – тип используемой функции потерь.
Список реализованных штрафных функций представлен
перечислением в классе CvGBTrees:
где для задачи восстановления регрессии предназначены функции:
enum {SQUARED_LOSS=0, ABSOLUTE_LOSS, HUBER_LOSS=3, DEVIANCE_LOSS};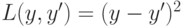 (SQUARED_LOSS),
(SQUARED_LOSS), 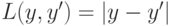 (ABSOLUTE_LOSS),
(ABSOLUTE_LOSS), 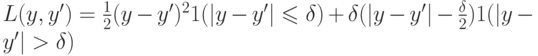 (HUBER_LOSS). Функция
(HUBER_LOSS). Функция 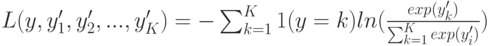 (DEVIANCE_LOSS) предназначена для решения задач
классификации на K классов. При использовании данного штрафа
строится K моделей в виде суммы деревьев, для оценки
вероятностей принадлежности объекта каждому из классов.
(DEVIANCE_LOSS) предназначена для решения задач
классификации на K классов. При использовании данного штрафа
строится K моделей в виде суммы деревьев, для оценки
вероятностей принадлежности объекта каждому из классов. - weak_count – количество обучаемых деревьев. В случае loss_function_type=DEVIANCE_LOSS фактическое количество деревьев, которое будет построено в K раз больше.
- shrinkage – скорость обучения, уменьшение которой позволяет бороться с переобучением модели.
- subsample_portion – доля выборки, используемая для обучения каждого дерева. Для построения дерева решений случайным образом (без возвращения) выбирается subsample_portion прецедентов обучающей выборки. Случайные подвыбороки могут улучшить качество модели, однако, неприменимы в случае небольшого числа имеющихся прецедентов.
Предсказания с помощью модели градиентного бустинга деревьев решений выполняет метод predict:
float predict( const Mat& sample,
const Mat& missing=Mat(),
const Range& slice=Range::all(),
int k=-1 ) const;
Рассмотрим параметры данного метода:
- sample – матрица-вектор признакового описания объекта.
- missing – матрица-вектор, содержащая маску пропущенных значений.
- slice – используемые для предсказания деревья (по умолчанию используются все). Может применяться для подбора оптимального количества деревьев без необходимости производить обучение заново.
- k – для loss_function_type=DEVIANCE_LOSS номер функции, значение которой следует вернуть. Если k=-1, возвращается предсказанное значение целевой переменной.
Сохранение и загрузка модели выполняется так же, как и в рассмотренных ранее алгоритмах.
Ниже приведен пример использования класса CvGBTrees для решения задачи бинарной классификации и иллюстрация полученного классификатора (см. рис. 10.4)
#include <stdlib.h>
#include <stdio.h>
#include <opencv2/core/core.hpp>
#include <opencv2/ml/ml.hpp>
using namespace cv;
// размерность пространства признаков
const int d = 2;
// функция истинной зависимости целевого признака
// от остальных
int f(Mat sample)
{
return (int)((sample.at<float>(0) < 0.5f &&
sample.at<float>(1) < 0.5f) ||
(sample.at<float>(0) > 0.5f &&
sample.at<float>(1) > 0.5f));
}
int main(int argc, char* argv[])
{
// объем генерируемой выборки
int n = 2000;
// объем обучающей части выборки
int n1 = 1000;
// матрица признаковых описаний объектов
Mat samples(n, d, CV_32F);
// номера классов (матрица значений целевой переменной)
Mat labels(n, 1, CV_32S);
// генерируем случайным образом точки
// в пространстве признаков
randu(samples, 0.0f, 1.0f);
// вычисляем истинные значения целевой переменной
for (int i = 0; i < n; ++i)
{
labels.at<int>(i) = f(samples.row(i));
}
// создаем маску прецедентов, которые будут
// использоваться для обучения: используем n1
// первых прецедентов
Mat trainSampleMask(1, n1, CV_32S);
for (int i = 0; i < n1; ++i)
{
trainSampleMask.at<int>(i) = i;
}
// будем обучать модель градиентного бустинга
// деревьев решений из 250 деревьев высоты 3 и
// скоростью обучения 0.5,без использования подвыборок.
// Т.к. решается задача классификации используем
// функцию потерь DEVIANCE_LOSS
CvGBTreesParams params; params.max_depth = 3;
params.min_sample_count = 1;
params.weak_count = 250;
params.shrinkage = 0.5f;
params.subsample_portion = 1.0f;
params.loss_function_type = CvGBTrees::DEVIANCE_LOSS;
CvGBTrees gbt;
Mat varIdx(1, d, CV_8U, Scalar(1));
Mat varTypes(1, d + 1, CV_8U, Scalar(CV_VAR_ORDERED));
varTypes.at<uchar>(d) = CV_VAR_CATEGORICAL;
gbt.train(samples, CV_ROW_SAMPLE,
labels, varIdx,
trainSampleMask, varTypes,
Mat(), params);
gbt.save("model-gbt.yml", "simpleGBTreesModel");
// вычисляем ошибку на обучающей выборке
float trainError = 0.0f;
for (int i = 0; i < n1; ++i)
{
int prediction =
(int)(gbt.predict(samples.row(i)));
trainError += (labels.at<int>(i) != prediction);
}
trainError /= float(n1);
// вычисляем ошибку на тестовой выборке
float testError = 0.0f;
for (int i = 0; i < n - n1; ++i)
{
int prediction =
(int)(gbt.predict(samples.row(n1 + i)));
testError +=
(labels.at<int>(n1 + i) != prediction);
}
testError /= float(n - n1);
printf("train error = %.4f\ntest error = %.4f\n",
trainError, testError);
return 0;
}


 "
"