|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Нейросетевые самообучающиеся системы управления
7.2. Нейросетевое воплощение
"
Медузин сел за письменный стол и просидел с час в глубокой задумчивости; потом вдруг "обошелся посредством" руки, схватил бумагу и
написал:
- Российская грамматика и логика






много употребл.
- История и география











употребляет довольно
- Чистая математика












плох
- Французский язык












. виноградн. много
- Немецкий язык













.. пива очень много
- Рисование и чистописание




.



.. одну настойку
- Греческий язык













.. все употребляет
После этих антропологических отметок Иван Афанасьевич записал соответственную им программу:
Ведро сантуринского














. 16 руб.
1/2 ведра настойки















.. 8 "
1/2 ведра пива

















.. 4 "
2 бутылки меду

















50 коп.
Судацкого 10 бутылок














10 "
3 бутылки ямайского














.. 4 "
Сладкой водки штоф














.. 2 " 50 коп.
_____________________
Итого: 45 руб."
Упражнение:
постройте нейросеть, позволяющую предсказывать действительные расходы учителя латинского языка и содержателя частной школы И.А. Медузина при оценке контингента гостей приближающегося дня тезоименитства.
Мы уже построили нейросеть для важной задачи принятия решений и вручили ее Заказчику – дяде Рамзаю. Однако, задумчиво глядя в синее небо под бодрящий рокот набегающей волны теплого течения Гольфстрим, мы не можем прогнать мыслей об обобщениях, вариациях и применениях…
Итак, еще раз тщательно проследим принцип динамического совмещения процесса обучения системы управления с процессом выдачи решений, изложенный выше, и установим в схеме на рис. 7.2 целесообразность, место и способ использования нейронной сети как основного реального средства искусственного интеллекта. Прежде всего, мы понимаем, что основным естественным и целесообразным местом применения нейросети здесь является база знаний, ранее реализованная с помощью ассоциативной памяти (рис. 7.1). Нам только надо позаботиться о том, чтобы "крутились" там не численные значения информации, а вес этой информации или ее достоверность. То есть не сама информация должна обрабатываться нейросетью, а ее логический эквивалент. Ведь мы поняли, что принцип искусственного интеллекта направлен на параллельную обработку логических высказываний, а вовсе не ориентирован напрямую на числовую обработку информации, как это делается при решении некоторых "нейроподобных" задач при использовании нейросети в роли спецпроцессора.
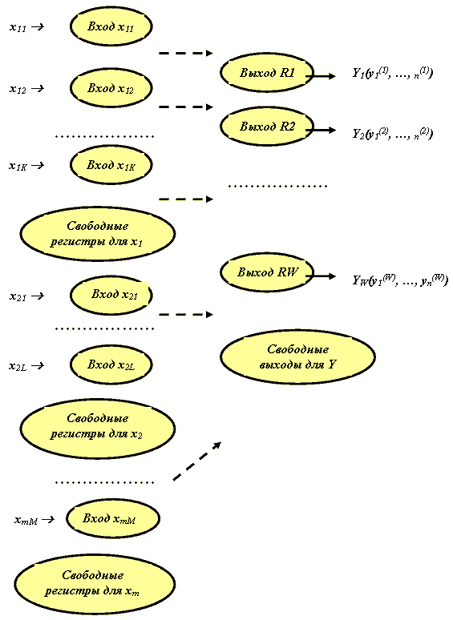
Пусть нейросеть в роли базы знаний имеет текущий вид, представленный на рис. 7.3.
Нейроны-рецепторы оказались закрепленными за значениями элементов входного вектора. Это значит, что в режиме обучения (или в процессе динамической корректировки) установилось соответствие на основе положения "величина возбуждения данного p -го нейрона входного слоя принимает значение достоверности того, что xi= xi(p) .
Здесь могут фигурировать не точные значения параметров, а некоторые диапазоны их изменения, как это указывалось в 3.2.
Как мы ранее делали, при обучении мы полагаем эту достоверность равной единице, а в процессе распознавания может быть что угодно, даже не удовлетворяющее свойству полноты событий.
"Показывая" сети на этапе обучения различные эталоны, методом трассировки мы можем добиться установления соответствия вида {Входы xi} -> Rq , наполнив тем самым базу знаний. Каждое решение Rq при этом тоже указывает на определенное значение вектора – результата Yq, компоненты которого суть управляющие воздействия системы. То есть нейроны Rq фактически закрепляются за ситуациями, по которым мы знаем векторы характеристик или значений параметров принимаемых решений – векторы значений управляющих воздействий.
Для нахождения этих значений управляющих воздействий в зависимости от значений исходных данных может быть использовано моделирование, наряду с экспериментом или с экспертными оценками. Таким образом, модель, эксперимент или эксперт играют роль учителя. (Мы ранее уже высказали сомнение насчет существования и действенности "чистого" самообучения.)
Первоначально обученная таким образом нейросеть может быть уже использована в рабочем режиме (распознавания) и в режиме совместной работы с моделью. При этом мы понимаем, что нейросеть обучена недостаточно, и, подобно пристрелке реперов "в свободное от работы" время, мы пытаемся с помощью модели испытать и, в случае необходимости, дополнить знания нейросети.
Модель случайно или направленно – по обоснованному плану "выбрасывает" некоторую ситуацию, характеризующуюся значением компонент входного вектора Х. По каждой компоненте определяется вес или достоверность того, что ее значение совпадает с подмножеством значений этой компоненты, представленных входным слоем нейросети, или с диапазонами значений этой компоненты.
Например, сеть "знает" реакцию на значение (опустим индекс) x = 2, x = 5, x = 6. Модель выбросила значение х = 5,7. Это может означать необходимость формирования значений возбуждения Vx=2 = 0 , Vx=5 = 0,3 , Vx=6 = 0,7 . Здесь индексы возбуждений указывают нейроны входного слоя, закрепленные за данным значением параметра. Так делается по всем компонентам входного слоя.
Пусть, "пройдя" по сети, данные возбуждения входного слоя привели к преодолению порога возбуждения нейронов выходного слоя R5 ( VR5 = a ), R7 ( VR7 = b ), R12 ( VR12 = c ). При этом нейрону R5 соответствует вектор управляющих воздействий Y5 = (y1(5), y2(5), ..., yn(5)) , нейрону R7 – вектор Y7 = (y1(7), ..., yn(7)) , нейрону R12 – вектор Y12 = (y1(12), ..., yn(12)) . Тогда мы находим предполагаемый ответ нейросети:
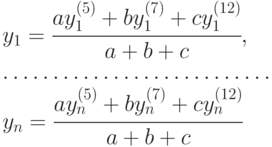
Подставляем данное решение в модель и устанавливаем, удовлетворяет ли нас оно, – например, по величине промаха. Если удовлетворяет, мы делаем положительный вывод об обученности нейросети и продолжаем ее испытание по другим исходным данным. Если нет – сеть необходимо "доучить", продемонстрировав самый высокий логический уровень обратной связи.
Для этого мы должны ввести в действие новые рецепторы, закрепив их за теми значениями исходных данных или их диапазонами, которые ранее не были представлены. Например, нам придется закрепить рецептор за значением х = 5,7.
Далее, мы должны выделить нейрон выходного слоя и закрепить его за соответствующим правильным решением, которое мы должны получить с помощью модели.
Далее, мы должны выполнить трассировку для того, чтобы задание нового эталона с единичной достоверностью исходных данных приводило к максимальному возбуждению выделенного нейрона выходного слоя, ответственного за получение правильного решения.
Таким образом, сеть может обучаться до тех пор, пока не перестанет давать "сбоев". А поскольку в вероятностном аспекте это вряд ли возможно, то в таком режиме она должна работать в течение всего жизненного цикла, реализуя известную пословицу "Век живи – век учись"…
Здесь наглядно представлена замечательная возможность нейросети: табличная аппроксимация функции многих переменных , снабженная процедурой интерполяции (экстраполяции) для нахождения произвольного значения вектора-аргумента и приближенного соответствующего значения векторной функции. При этом входной вектор возбуждений рецепторов преобразуется в максимальное или усредненное значение возбуждения нейронов выходного слоя, указывающего на соответствующее значение вектора-функции. Так что практически столь простым способом мы построили аппроксимацию векторной функции от векторного аргумента!
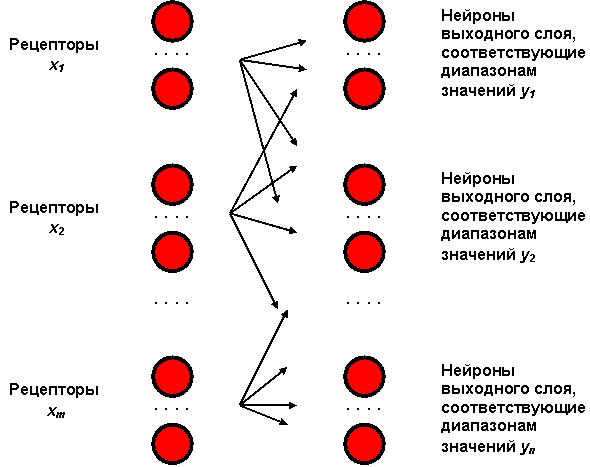
Такую аппроксимацию можно выполнить и "в более явном виде", ибо каждая компонента yj решения Y = {y1,..., yп} может отыскиваться отдельно в результате предварительной трассировки (рис. 7.4). То есть сеть может быть построена и обучена так, чтобы заданное значение Х = {x1,..., xт} приводило к максимальному (или усредненному) значению возбуждения нейрона выходного слоя, указывающего соответствующее значение y1 , к максимальному (или усредненному) значению возбуждения другого нейрона выходного слоя, указывающего на значение у2 и т.д. Выходной слой оказывается разбит на области, каждая из которых закреплена за своим параметром уi , i =1,..., п. Тогда полученное преобразование можно условно записать X -> {Вых(у1), Вых(у2),..., Вых(уп)} .
Следует обратить внимание не только на высокую производительность такого рода самообучающихся систем в рабочем режиме, но и на их адаптивность, развиваемость, живучесть и т.д.